Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Енергія кінетична та потенціальна. Закон збереження енергіїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У механіці розрізняють два види енергії: кінетичну Кінетичною енергією тіла називають енергію, яка є мірою його меха-нічного руху. Кінетична енергія рухомого тіла кількісно дорівнює роботі, яку може виконати тіло проти гальмівної сили при гальмуванні його до пов-ної зупинки:
Знак "–" вказує на те, що при гальмуванні тіла його прискорення
Отже, кінетична енергія тіла і системи тіл дорівнює відповідно:
і є функцією стану руху тіл. Якщо на тіло (або систему тіл) діють консервативні сили, то мож-на ввести поняття потенціальної енергії тіла (або системи тіл). Оскільки робота сил такого поля не залежить від форми траєкторії, а визначається тільки кінцевими точками шляху, то вона є важливою фізичною величиною, що характеризує силове поле. Роботу сил поля по переміщенню тіла з точки 1 у точку 0 (рис.5.2) позначимо через
Тоді, згідно з визначенням поняття консервативних сил, робота сил поля по переміщенню тіла із точки 1 у точку 2 буде:
Рис.5.2
Для нескінченно малих переміщень:
Таким чином, робота, виконана над тілом консервативними силами, дорівнює зміні потенціальної енергії тіла, узятій із протилежним знаком. Оскільки
Величину сили знаходимо за співвідношенням:
а силу як вектор знайдемо через компоненти та орти:
Сила дорівнює градієнту потенціальної енергії. Градієнтом називають вектор, що показує напрямок найшвидшої монотонної зміни деякої вели-чини, значення якої змінюється від однієї точки простору до іншої. З рів-нянь (5.7) і (5.11) знаходимо:
Отже:
Це і є закон збереження повної енергії замкненої механічної системи, тобто окремий випадок одного з фундаментальних законів природи, у від-повідності з яким повна енергія замкненої системи при будь-яких процесах залишається незмінною.
Швидкість механічної системи і її положення в просторі залежать від вибору системи відліку, тобто є відносними. Це означає, що кінетична і по-тенціальна енергія системи самі по собі є відносними і визначаються лише з точністю до постійних величин, тобто визначається лише зміна цих видів енергії внаслідок участі системи в тих або інших процесах. Закон збережен-ня енергії вказує на те, що в замкнених системах можливі лише такі проце-си, при яких один вид енергії може перетворюватися на інший зі збережен-ням незмінної повної енергії. У цьому й проявляється єдність матеріального світу. Зіткнення двох тіл Прикладом використання законів збереження імпульсу та енергії замкненої системи тіл може бути розгляд зіткнення двох тіл. Для спрощен-ня викладу розглянемо центральний удар двох тіл. Удар називають цент-ральним, якщо центри інерції тіл до удару рухалися уздовж прямої, що про-ходить через ці центри.Існує два граничних види удару: абсолютно непруж-ний та абсолютно пружний. При абсолютно непружному ударі кінетична енергія тіл повністю або частково перетворюється на внутрішню енергію; після удару тіла або зупи-няються, або рухаються з однаковою швидкістю. При цьому зберігається повна енергія системи, що складається з потенціальної енергії системи у зовнішніх потенціальних полях, кінетичної енергії системи та її внутріш-ньої енергії U. Внутрішня енергія тіла визначається станом руху й взаємним розташуванням мікрочастинок, з яких складається це тіло. З погляду меха-ніки внутрішня енергія тіла складається з кінетичної енергії механічного руху мікрочастинок тіла і потенціальної енергії взаємодії цих частинок. При ударі відбувається взаємне перетворення кінетичної та внутрі-шньої енергії тіл; потенціальна енергія тіл у зовнішніх потенціальних полях у процесі самого удару не змінюється. Тому цей вид енергії системи надалі не розглядається. Якщо кінетична енергія тіл у результаті удару повністю перетворю-ється на внутрішню, то тіла зупиняються, а внутрішню енергію U системи після зіткнення знаходимо як суму кінетичних енергій тіл:
Якщо кінетична енергія перетворюється на внутрішню лише частково, а тіла після зіткнення рухаються з однаковою швидкістю
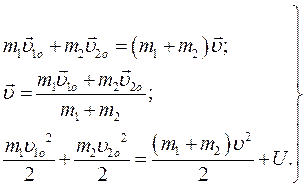
При абсолютно пружному ударі кінетична енергія перетворюється повністю або частково на внутрішню енергію пружної деформації, а потім при відштовхуванні тіл знову на кінетичну. При повному переході кінетичної енергії у внутрішню тіла відразу після взаємодії зупиняються, а при зворотному перетворенні енергії руха-ються окремо з різними швидкостями. Закони збереження імпульсу і енергії в цьому випадку описуються рівняннями:
При неповному перетворенні кінетичної енергії на внутрішню отримаємо:
Розв’язуючи системи рівнянь (5.18) і (5.19), можна знайти невідомі величини U,
Приклад розв’язування задач Дві ідеально пружні кульки масами m 1 та m 2 рухаються уздовж однієї й тієї самої прямої зі швидкостями Розв’язування Оскільки кулі виконують абсолютно пружний удар із частковим пере-творенням кінетичної енергії на внутрішню, то для знаходження потенці-альної енергії деформації (тобто зміни внутрішньої енергії системи куль) необхідно скористатися законами збереження імпульсу та енергії системи куль:
Тут З першого рівняння знаходимо швидкість
|
||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 704; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.246.20 (0.011 с.) |

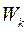 і потен-ціальну
і потен-ціальну  .
.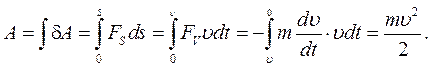 (5.7)
(5.7)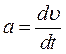 від’ємне; межі інтегрування визначаються швидкістю руху тіла в момент визначення його кінетичної енергії і повною зупинкою. Для системи
від’ємне; межі інтегрування визначаються швидкістю руху тіла в момент визначення його кінетичної енергії і повною зупинкою. Для системи 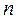 тіл рівняння (5.7) набирає вигляду:
тіл рівняння (5.7) набирає вигляду: (5.8)
(5.8)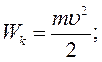
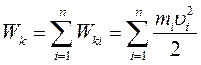 (5.9)
(5.9)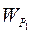 ,а з точки 2 у точку 0 – через
,а з точки 2 у точку 0 – через  ;
;  ;
; 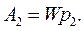
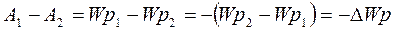 . (5.10)
. (5.10)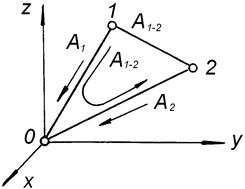
 . (5.11)
. (5.11)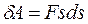 , то
, то  , а компоненти сили можуть бути виражені рівняннями:
, а компоненти сили можуть бути виражені рівняннями: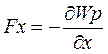 ;
;  ;
;  . (5.12)
. (5.12)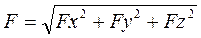 , (5.13)
, (5.13)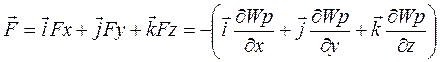 ;
;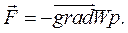 (5.14)
(5.14)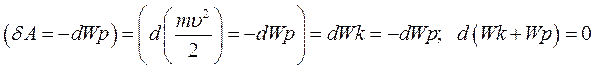 .
.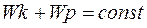 . (5.15)
. (5.15)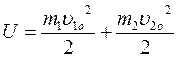 . (5.16)
. (5.16)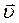 , то після зіткнення тіл за законами збереження імпульсу й енергії можна знайти невідомі величини
, то після зіткнення тіл за законами збереження імпульсу й енергії можна знайти невідомі величини 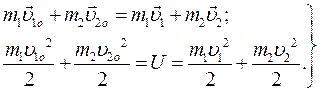 (5.18)
(5.18) (5.19)
(5.19)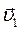 та
та 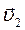 у кожному конкретному випадку. При цьому закон збереження імпульсу варто застосовувати в проекціях на напрямок руху.
у кожному конкретному випадку. При цьому закон збереження імпульсу варто застосовувати в проекціях на напрямок руху. і
і  .Під час зіткнення кульки почи-нають деформуватися й частина кінетичної енергії перетворюється на по-тенціальну енергію деформації. Потім деформація зменшується, а запасена потенціальна енергія знову перетворюється на кінетичну. Знайти значення максимальної потенціальної енергії деформації.
.Під час зіткнення кульки почи-нають деформуватися й частина кінетичної енергії перетворюється на по-тенціальну енергію деформації. Потім деформація зменшується, а запасена потенціальна енергія знову перетворюється на кінетичну. Знайти значення максимальної потенціальної енергії деформації.
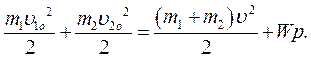
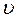 – швидкість спільного руху максимально деформованих куль.
– швидкість спільного руху максимально деформованих куль.