
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Д.4 Використання теореми про зміну кінетичного моменту для дослідження руху матеріальної системиСодержание книги
Поиск на нашем сайте
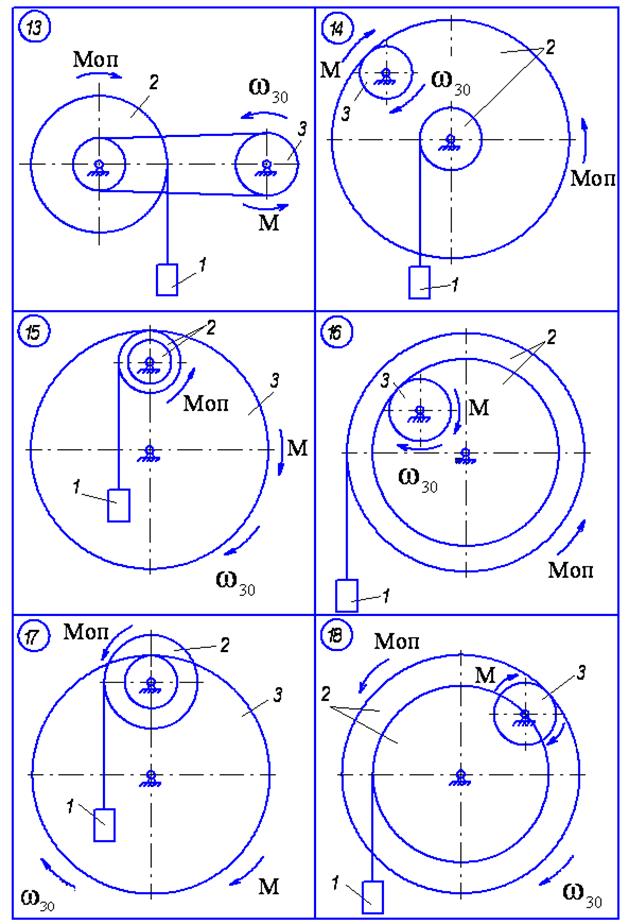
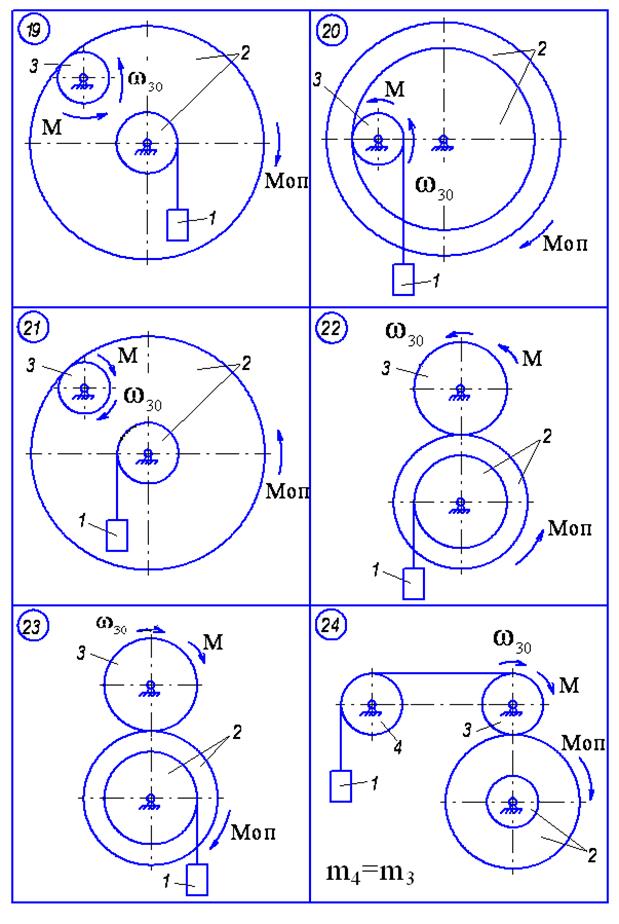
Матеріальна система (рис. 4.1-4.5) приводиться до руху моментом М, що прикладений до однорідного тіла 3. Знайти закон руху тіла 1, якщо на тіло 2 діє постійний момент опору М. В початковий момент часу кутова швидкість тіла 3 - w30. Масами пасів та їх ковзанням по шківах знехтувати. Тіла 2 та 3 обертаються навколо горизонтальних осей. Дані для розрахунку наведені в таблиці 4.1. Де R2, r2, R3 – розміри тіла 2 та 3; і2 – момент інерції тіла 2 відносно осі обертання; m1, m2, m3 – маси тіл 1, 2 та 3.
Таблиця 4.1
Рисунок 4.2
Рисунок 4.3
Рисунок 4.4
Рисунок 4.5 Приклад виконання завдання
До вантажу 1 (рис. 4.6) масою m1=20кг прив’язаний трос, який перекинутий через нерухомий блок 4 і другий кінець якого закріплений на поверхні шківа 2 радіусом r2 (m2 = 2кг). Механічна система приводиться до руху моментом Знайти закон руху вантажу 1, якщо на тіло 2 діє момент опору МОП = 15 Н×м і при t = 0 кутова швидкість тіла
Рисунок 4.6
Розв’язання. Розглянемо окремо рух тіл 2 і 3 та механізму наведеного на рис. 4.6 До тіла 3 (рис. 4.7) прикладені зовнішні сили: пара сил з моментом М, сила тяжіння P3=m3g, реакції циліндричного шарніра X3 і Y3, реакції тіла 2 – колове зусилля S3 і сила нормального тиску N3.
Запишемо диференціальне рівняння обертання тіла 3 навколо нерухомої осі враховуючи, що якщо момент зовнішніх сил діє у напрямку руху тіла, тоді записуємо його з додатним знаком.
де
Таблиця 4.2 - Осьові моменти інерції однорідних тіл
Рисунок 4.7
Початкові умови: при t=0, На тіло 2 (рис. 4.8) діють такі зовнішні сили: сила тяжіння P2=m2g, реакції циліндричного шарніра X2 та Y2, натяг троса S2 (трос працює тільки на розтяг), реакції тіла 3 – Диференціальне рівняння обертання тіла 2 (рис. 4.8) навколо горизонтальної осі Z.
де Оскільки
До тіл 1 та 4 (рис. 4.9) прикладені зовнішні сили: сили тяжіння P1=m1g та P4=m4g, реакція троса
Рисунок 4.8
Теорема про зміну кінетичного моменту для тіл 1 та 4 (рис. 4.9) в проекціях на вісь Z запишеться:
де LZ – кінетичний момент системи тіл 1 та 4 відносно осі Z,
Рисунок 4.9 Кінетичний момент LZ складається із моменту кількості руху LZ1 тіла 1 та кінетичного моменту LZ4 тіла 4 відносно осі Z LZ1 = m1V1R4, (4.6) LZ4 = IZ4ω4. (4.7) Враховуючи, що
Тепер диференціальне рівняння (4.5) набуває вигляду
Якщо до диференціальних рівнянь (4.1), (4.4), (4.8) додати кінематичні співвідношення
тоді отримаємо систему шести рівнянь в які входять невідомі: Розв’язуючи систему рівнянь (4.1), (4.4), (4.8), (4.9) маємо:
З урахуванням того, що m1=20кг, m2=2кг, m3=m4=3кг, r2=0,2м, R2=0,4м, і2=0,3м, R3=R4=0,3м, М = (16+11t2)
Для визначення закону руху тіла 1, інтегруємо двічі диференціальне рівняння (4.10), беручи до уваги початкові умови (4.2)
Перший інтеграл диференціального рівняння (4.10)
Закон руху тіла 1:
Відповідь:
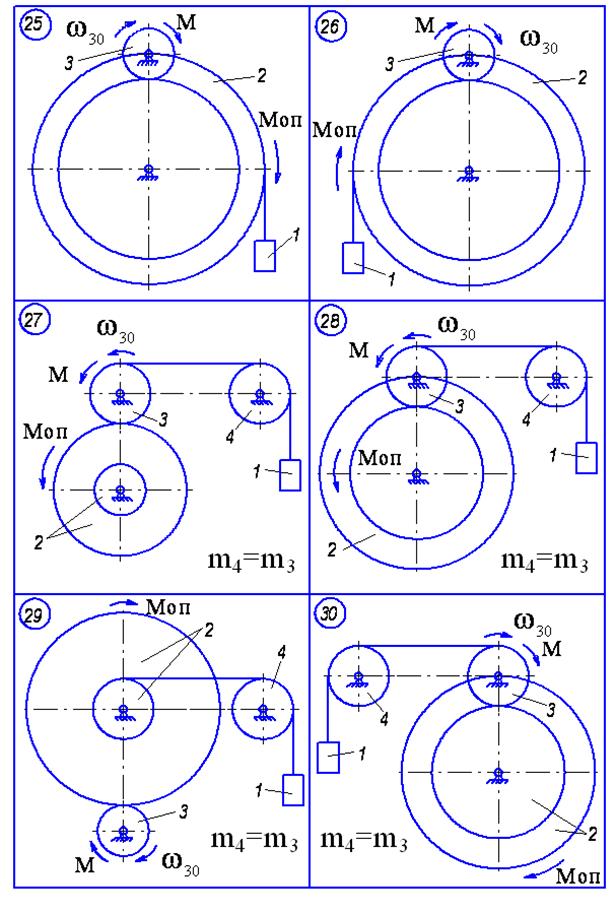
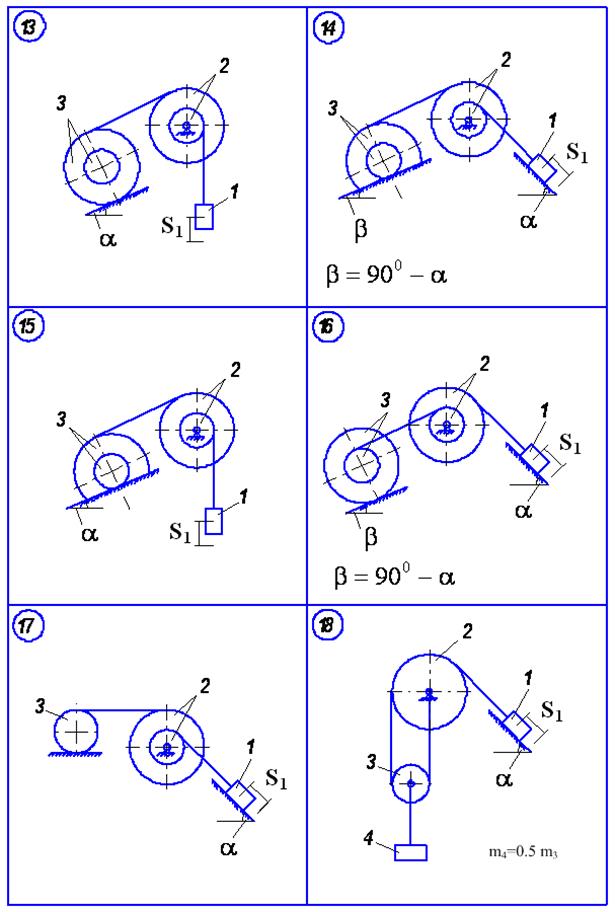
Д.5 Використання теореми про зміну кінетичної енергії для вивчення руху матеріальної системи Матеріальна система(рис.5.1-5.5) рухається із стану спокою під дією сили тяжіння. Знайти прискорення та швидкість тіла 1 у момент часу, коли воно пройде шлях S (S1=0.4м). Масами шнурів, силами опору в шарнірах знехтувати. Тіла котяться по поверхнях без ковзання. Величини для розрахунків наведені в табл. 5.1, де прийнято такі позначення: m1,m2,m3 – маси тіл 1, 2, 3; R2, r2, R3, r3 — найбільші та найменші розміри ступінчастих шківів тіл 2 та 3; ρ2x, ρ3x — радіуси інерції ступінчастих шківів 2 та 3 відносно осі обертання; α, β кути нахилу площин до горизонту. Якщо тіла 2 або 3 однорідні, тоді при розрахунках брати відповідно R2, R3. Шнури над похилими площинами паралельні цим площинам.
Таблиця 5.1
Рисунок 5.1
Рисунок 5.2
Рисунок 5.3
Рисунок 5.4
Рисунок 5.5 Приклад виконання завдання
Визначити прискорення та швидкість центра мас тіла 1 у момент часу, коли він пройде шлях S1, якщо матеріальна система (рис.5.6) починає рухатися із стану спокою. Масами шнурів знехтувати. Тіла 1 та 3 рухаються без ковзання. Дано: m1=10 кг, m2=2 кг, m3=1 кг, R2=0,4 м, r2=0,3м, R3=0,3 м, r3=0,2 м, ρ2=0,35 м, ρ3=0,25 м, α=30˚, β=45˚, S1=0,4 м.
Рисунок 5.6
Розв’язання. Для дослідження руху матеріальної систем (рис.5.6) застосуємо теорему про зміну кінетичної енергії механічної системи в диференціальній формі.
де Т — кінетична енергія системи при 0<х≤S1; ∑Nі та ∑Nе− сума потужностей внутрішніх та зовнішніх сил системи. Матеріальна система (рис.5.6) складається із твердих тіл та нерозтяжних шнурів, тоді
∑ Nі=0. (5.2)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.107.136 (0.01 с.) |

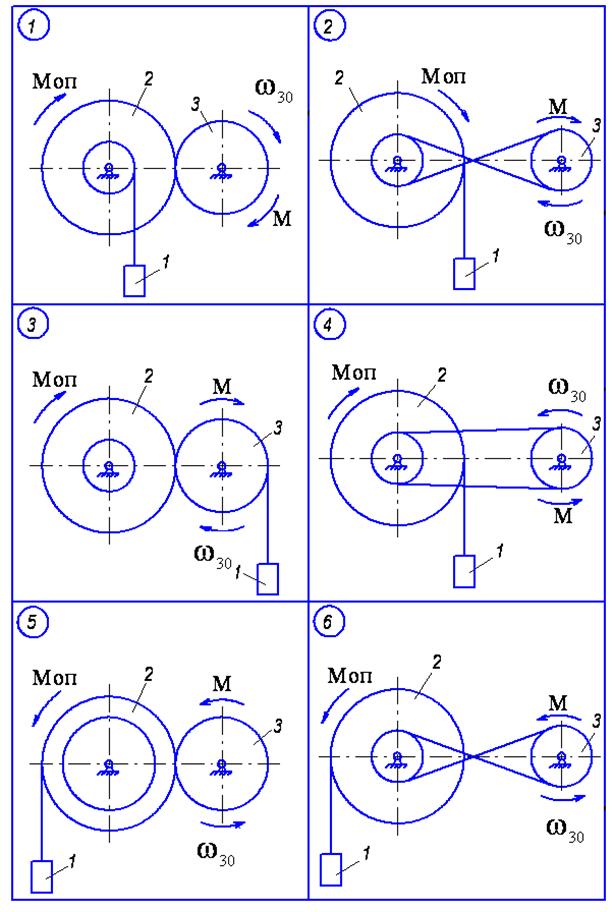 Рисунок 4.1
Рисунок 4.1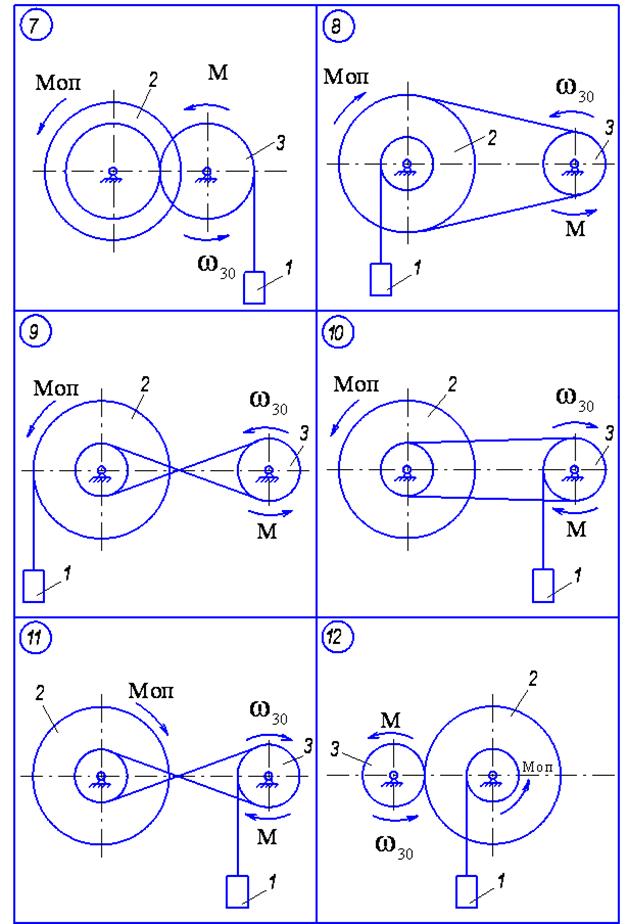
 , прикладеним до східчастого шківа 3 масою m3=3кг.
, прикладеним до східчастого шківа 3 масою m3=3кг. . Більший радіус у шківа 2 - R2=0,4м, менший – r2 = 0,2м, радіус інерції – і2 = 0,3м. Тіла 3 та 4 мають однакові маси m3=m4 і розміри R3 = R4 = 0,3м. Тіла 2,3 та 4 обертаються навколо горизонтальних нерухомих осей, а тіло 1 переміщується поступально.
. Більший радіус у шківа 2 - R2=0,4м, менший – r2 = 0,2м, радіус інерції – і2 = 0,3м. Тіла 3 та 4 мають однакові маси m3=m4 і розміри R3 = R4 = 0,3м. Тіла 2,3 та 4 обертаються навколо горизонтальних нерухомих осей, а тіло 1 переміщується поступально.
 ,
, - момент інерції тіла відносно осі z;
- момент інерції тіла відносно осі z; - кутове прискорення тіла 3;
- кутове прискорення тіла 3; - момент зовнішніх сил, прикладених до тіла 3, відносно осі z.
- момент зовнішніх сил, прикладених до тіла 3, відносно осі z.

















 . (4.1)
. (4.1) ,
, 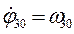 . (4.2)
. (4.2) та
та  , які за третім законом Ньютона направлені в протилежні сторони сил S3 та N3 (рис. 4.7).
, які за третім законом Ньютона направлені в протилежні сторони сил S3 та N3 (рис. 4.7). , (4.3)
, (4.3) - момент інерції тіла 2 відносно осі Z.
- момент інерції тіла 2 відносно осі Z. , то рівняння (4.3) запишеться у вигляді
, то рівняння (4.3) запишеться у вигляді . (4.4)
. (4.4) , реакції циліндричного шарніра X4 та Y4.
, реакції циліндричного шарніра X4 та Y4.
 , (4.5)
, (4.5) - головний момент зовнішніх сил.
- головний момент зовнішніх сил.
 , а
, а  , кінетичний момент системи LZ визначимо за формулою
, кінетичний момент системи LZ визначимо за формулою
 . (4.8)
. (4.8)

 (4.9)
(4.9)
 .
. , M0=15
, M0=15  , отримаємо
, отримаємо . (4.10)
. (4.10)

 м.
м.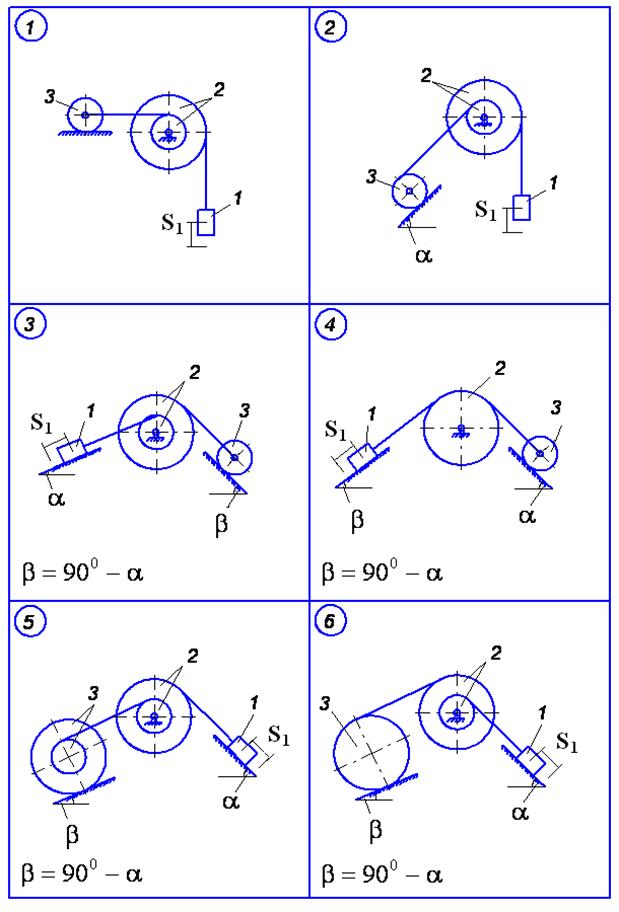




 =∑Nе+∑Nі, (5.1)
=∑Nе+∑Nі, (5.1)


