
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Д.2 Використання теореми про рух центра мас для визначення переміщення тілСодержание книги
Поиск на нашем сайте
Визначити переміщення призми 1 (рис. 2.1-2.5) по горизонтальній гладенькій поверхні, якщо центр мас тіла 2 опустився на відстань S відносно призми 1 (схеми 1-19) або тіло 2 повернулося на заданий кут навколо горизонтальної осі (схеми 20-30). В початковий момент часу матеріальна система знаходиться у спокої. Дані для розрахунків наведені в табл. 2.1 (
Таблиця 2.1
Рисунок 2.2
Рисунок 2.4 Приклад виконання завдання По похилій площині (рис. 2.6) призми 1 масою m1=10кг спускається вантаж 2 (m2=6кг), який тягне за допомогою невагомої нитки вантаж 3 масою m3=4кг. Знайти переміщення призми 1 по гладенькій горизонтальній площині, якщо тіло m2 опустилось по похилій площині на S=0,5м. Розв’язання. Покажемо зовнішні сили, які прикладені до матеріальної системи, що складається з призми 1 та тіл 2, 3. Такими силами є: P1=m1g – сила ваги призми, P2=m2g i P3=m3g – вага відповідно другого та третього вантажів, N – реакція гладенької горизонтальної поверхні.
Рисунок 2.6
Запишемо теорему про рух центра мас матеріальної системи в проекціях на вісь Х:
де Оскільки В початковий момент часу система знаходилась у спокої і тому
Таким чином, координата ХС центра мас матеріальної системи залишається сталою незалежно від переміщень тіл, що входять у систему. Визначимо положення центра мас системи в початковий момент часу:
Якщо вантаж 2 переміститься на величину
Враховуючи (2.2), із формули (2.3) отримаємо:
Переміщення
Тепер із формули (2.4) знаходимо переміщення призми.
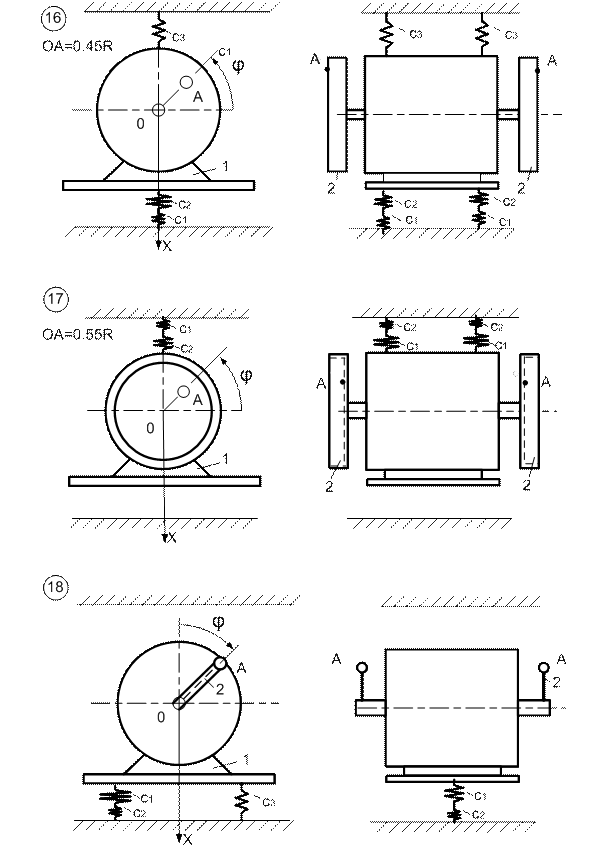
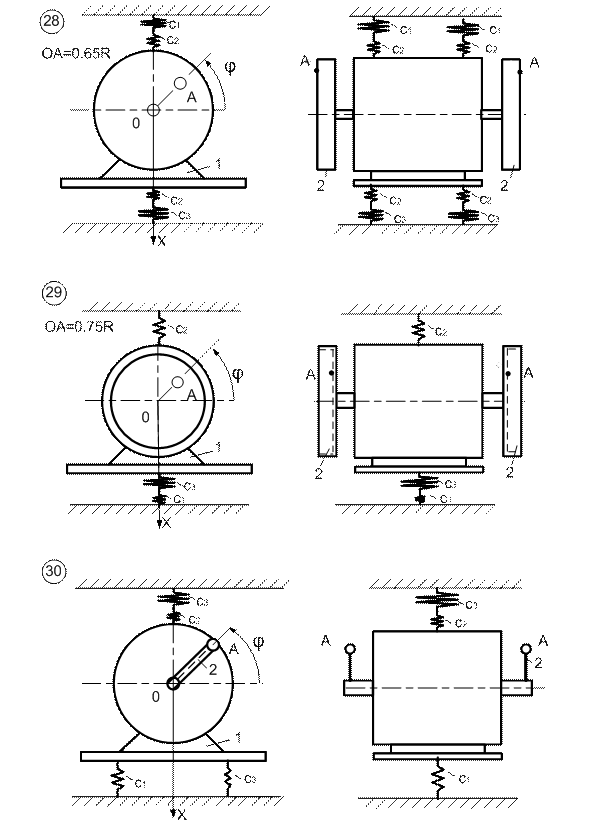
Знак “мінус” вказує на те, що призма 1 перемістилася в сторону, протилежну додатному напрямку осі Х. Відповідь: призма 1 перемістилась вправо на 0,229 м. Д. 3 Використання теореми про зміну головного вектора кількості руху системи для дослідження переміщення тіл Електродвигун 1 (рис. 3.1 – 3.10) масою m1 приєднується до системи нездеформованих пружин. На тілі 2 масою m2 (однорідний диск радіуса R – варіант 1, 4, 7, 10, 13, 16, 19, 22, 25, 28; кільце радіуса R – варіант 2,5,8,11,14,17,20,23,26,29; однорідний стержень ОА = R – варіант 3,6,9,12,15,18,21,24,27,30), що з’єднане з ротором електродвигуна 1, закріплена матеріальна точка масою mА на відстані ОА від осі ротора електродвигуна. Ротор обертається з постійною кутовою швидкістю ω. Пружини приєднані до електродвигуна таким чином, що його статор переміщується поступально, а точка 0 по осі х Знайти закон руху корпуса електродвигуна, центр мас якого О переміщується по вертикалі, побудувати графік руху точки О протягом одного періоду при кутовій швидкості ω = n∙ ρ (ρ – частота, при якій спостерігається явище резонансу), якщо в початковий момент часу точка О зміщена із положення рівноваги на величину λ0 і їй була надана швидкість ν0, а тіло 2 почало обертатись навколо горизонтальної осі О з кутовою швидкістю ω. Необхідні для розрахунку дані наведені в табл. 3.1. Таблиця 3.1
Рисунок 3.1
Рисунок 3.2
Рисунок 3.3
Рисунок 3.4
Рисунок 3.5
Рисунок 3.6
Рисунок 3.7
Рисунок 3.8
Рисунок 3.9
Рисунок 3.10 Приклад виконання завдання Система тіл (рис. 3.11) до якої входить електродвигун 1 масою m2 = 20 кг, однорідний стержень 2 масою m2 = 2 кг та довжиною Система пружин жорсткістю С1=2·103Н/м, С2=3·103Н/м, та С3=4·103Н/м знаходиться у положенні статичної рівноваги. В деякий момент часу точку О зміщують із положення рівноваги вверх на х0=2см і надають швидкість ν0 = 3 м/с вертикально вниз. Одночасно ротор електродвигуна починає обертатись із постійною кутовою швидкістю ω = 1/2·ρ (ρ – частота збурювальної сили) навколо горизонтальної осі. Знайти закон та побудувати графік (при
Рисунок 3.11
Розв’язання. Систему пружин замінюємо однією еквівалентною пружиною жорсткістю С
де С13 = С1·С3 /(С1+С3) = 2·103·4·103/(2·103+4·103) = 4/3·103 Н/м.

Рисунок 3.12
Розглянемо рух невільної системи тіл (рис. 3.11): електродвигуна 1, двох однорідних стержнів 2, двох матеріальних точок А. Центр мас О електродвигуна зміщений із положення статичної рівноваги
Fпр= С· (х+λ), (3.1) де λ – статична деформація пружин, яка знаходиться за формулою λ= (P1+2P2+2PA) /C, де P1,P2,PA – вага відповідно тіл 1,2 та матеріальної точки А. Кутова швидкість обертання ротора
оскільки при явищі резонансу частота збурювальної сили p дорівнює власній частоті коливань системи k= Для дослідження руху корпуса електродвигуна (рис.3.12) використаємо теорему про зміну головного вектора кількості руху системи в проекції на вісь х.
Проекція Qх головного вектора кількості руху системи на вісь х
Використовуючи теорему додавання швидкостей, отримаємо проекцію швидкості точки А і швидкості центра мас тіл 2 на вісь х (рис.3.12).
де Тепер формула (3.4), враховуючи (3.5), запишеться: Qх=
Підставляючи значення Qх (3.6) та Fxe (3.3) в теорему (3.2), отримаємо диференціальне рівняння:
Або
Розв’язок неоднорідного диференціального рівняння (3.7) складається із загального розв’язку однорідного диференціального рівняння
х1=B1coskt + B2 sinkt (3.8)
та частинного розв’язку х2 неоднорідного диференціального рівняння (3.7), який будемо шукати у вигляді:
х2=B3 cosωt. (3.9)
Із (3.7) враховуючи (3.9), знаходимо B3
- ω2B3cosωt + k2B3cosωt = h0cosωt,
Розв’язок неоднорідного диференціального рівняння (3.7)
Постійні інтегрування B1 та B2 визначимо із початкових умов:
Швидкість V точки О (рис.3.12)
Із рівнянь (3.10), (3.12) та початкових умов (3.11) знаходимо постійні інтегрування B1 та B2 . -0,02 = B1+0,007, 3 = 22,86 B2. B2 = 0,13 м; B1 = -0,027м. Тепер рівняння (3.10) руху точки О електродвигуна запишеться: x=-0,027cos(22,86t) +0,13sin(22,86t)+0,007cos(11,43t). (3.13)
Рисунок 3.13
На рис.3.13 наведений графік руху точки О корпуса електродвигуна, який отриманий на підставі формули (3.13).
Відповідь:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.80.194 (0.009 с.) |

 ).
).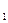 ,кг
,кг
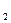 ,кг
,кг
 град
град
 l,
м
l,
м
 Рисунок 2.1
Рисунок 2.1



 Рисунок 2.5
Рисунок 2.5
 , (2.1)
, (2.1) ,
,  - проекція головного вектора зовнішніх сил на вісь Х.
- проекція головного вектора зовнішніх сил на вісь Х. = 0. Тоді
= 0. Тоді  .
. . Із формули (2.1) маємо:
. Із формули (2.1) маємо: .
. . (2.2)
. (2.2) , тоді тіло 3 – на
, тоді тіло 3 – на  , а призма 1 -
, а призма 1 -  і положення ХС центра мас знайдемо за формулою:
і положення ХС центра мас знайдемо за формулою: . (2.3)
. (2.3) . (2.4)
. (2.4) та
та 














 м, матеріальна точка масою mА= 0,5 кг, яка знаходиться в точці А (ОА=2/3
м, матеріальна точка масою mА= 0,5 кг, яка знаходиться в точці А (ОА=2/3  ).
). , де T – період) руху центра мас (точка О) електродвигуна.
, де T – період) руху центра мас (точка О) електродвигуна.
 ,
,
 на величину х (рис. 3.12), а стержні 2 повернулися на кут φ навколо горизонтальної осі О. Дію в’язі (пружину жорсткістю С) замінюємо реакцією в’язі – силою Fпр. Оскільки в точці
на величину х (рис. 3.12), а стержні 2 повернулися на кут φ навколо горизонтальної осі О. Дію в’язі (пружину жорсткістю С) замінюємо реакцією в’язі – силою Fпр. Оскільки в точці  деформація пружин дорівнює нулю, то
деформація пружин дорівнює нулю, то ,
, (m – маса системи)
(m – маса системи) (3.2)
(3.2) ,
,  (3.3)
(3.3) . (3.4)
. (3.4) (3.5)
(3.5) ,
, .
. (
(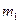 +2m 2 +2m
+2m 2 +2m  )-(
)-(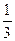 m 2 +
m 2 +  m
m  (3.6)
(3.6) .
. , (3.7)
, (3.7)
 1 +
1 +  х1 =0, а саме:
х1 =0, а саме: .
.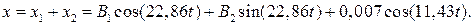 (3.10)
(3.10) .(3.11)
.(3.11)





