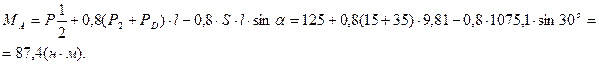Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення зусиль в пасах та між тіламиСодержание книги
Поиск на нашем сайте
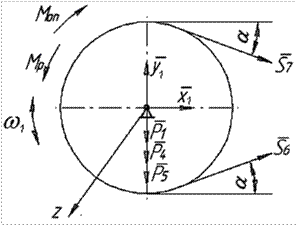
Розглянемо окремо рух кожного тіла матеріальної системи (рис. 6.11).
Рисунок 6.13 Запишемо диференціальне рівняння обертання тіла 1 (рис. 6.13) навколо нерухомої осі Z.
Необхідно врахувати, що момент сили або пари сил буде додатним, якщо він діє у напрямку руху тіла. Так, у рівнянні (6.9) момент сили На тіло 2 (рис. 6.14) під час руху діють зовнішні сили: сила тяжіння У диференціальному рівнянні руху тіла 2 (рис. 6.14) навколо горизонтальної осі Z
сили
Рисунок 6.14 Для тіла 3 (рис. 6.15), що переміщується під дією сили тяжіння
Звичайно Із диференціальних рівнянь (6.10) - (6.11) знаходимо (
При t1=1,5с S2=-300(9,81+3,74)=-4065н.
S7=24478,0н.
Рисунок 6.15 За законом Амонтона-Кулона
Звідки:
Визначення реакції циліндричних шарнірів Для тіла 1 та 2 запишемо теорему про рух центра мас в проекціях на осі X та Y. Тіло 1 (рис. 6.13)
Тіло 2 (рис. 6.14)
В рівнянні (6.12) – (6.13) Отримали систему рівнянь
в якій невідомі величини: x1, y1, x2, y2. Розв’язуючи систему рівнянь (6.14), отримаємо
де
При t1=1,5с.
Відповідь:
Принцип Д’Аламбера
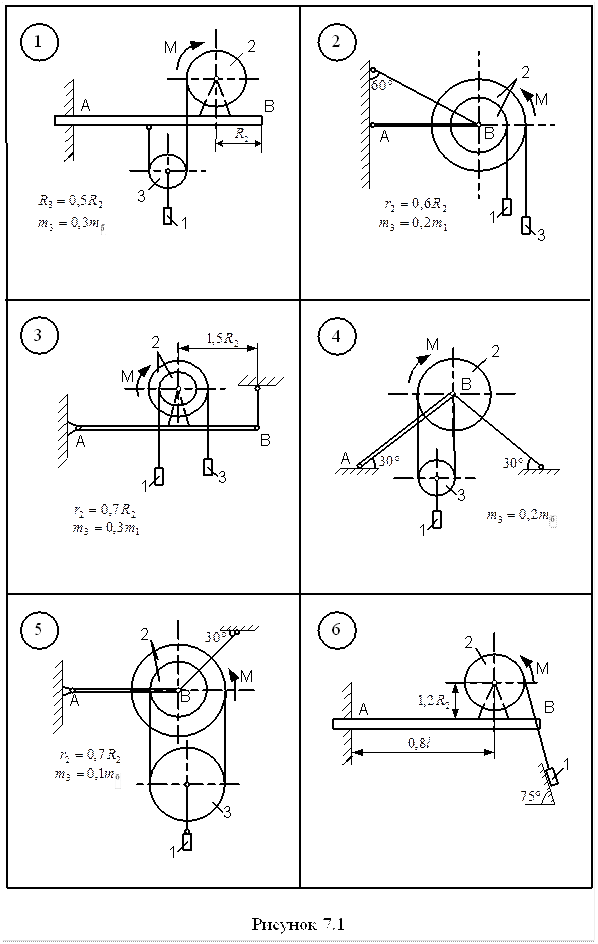
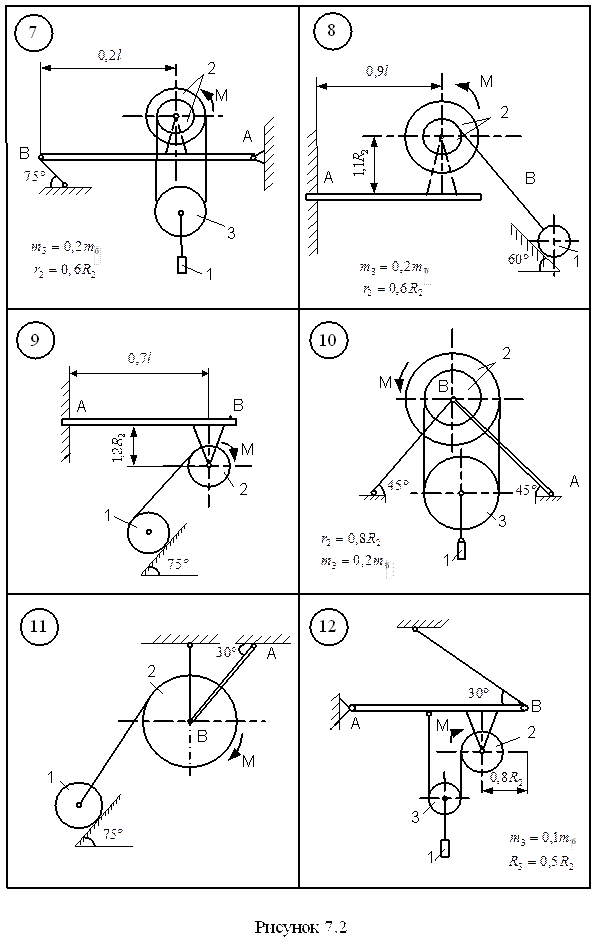
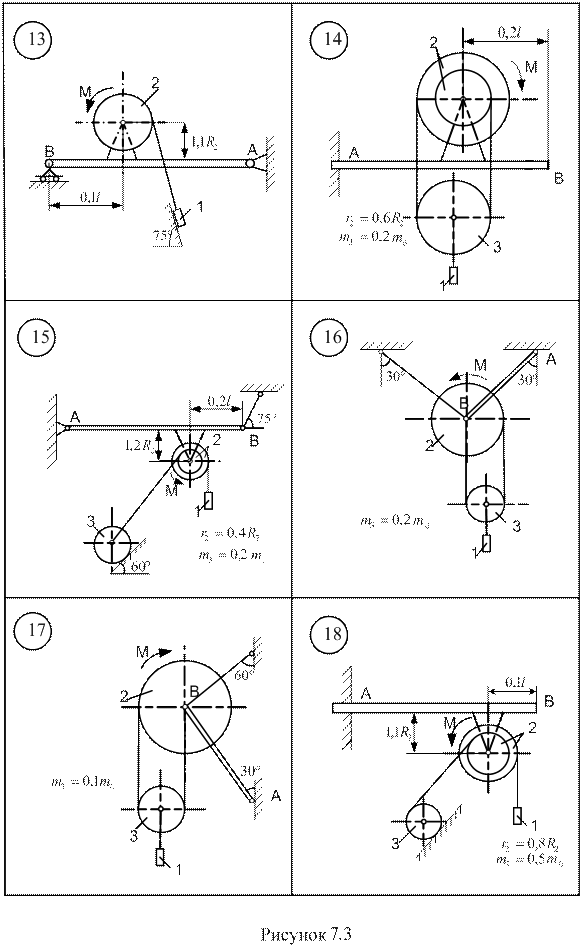
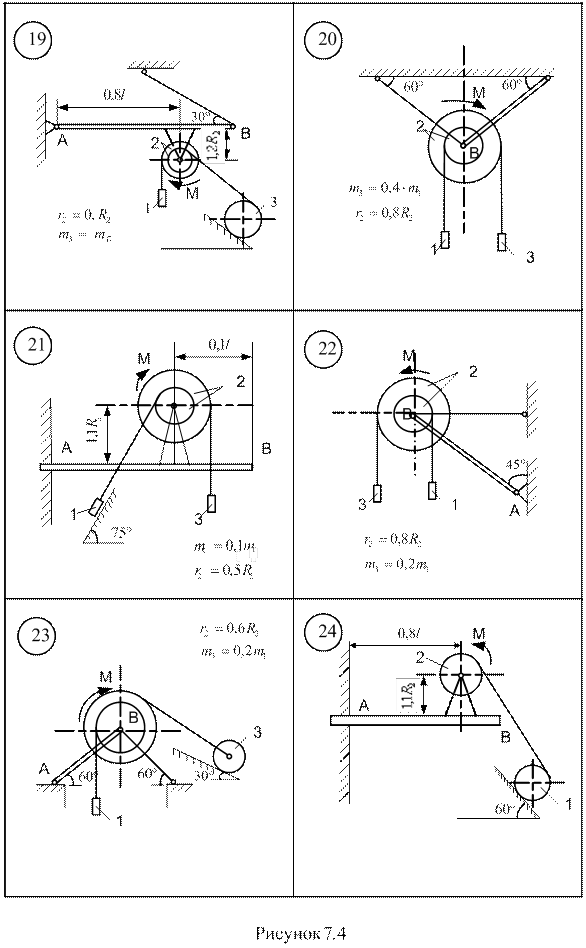
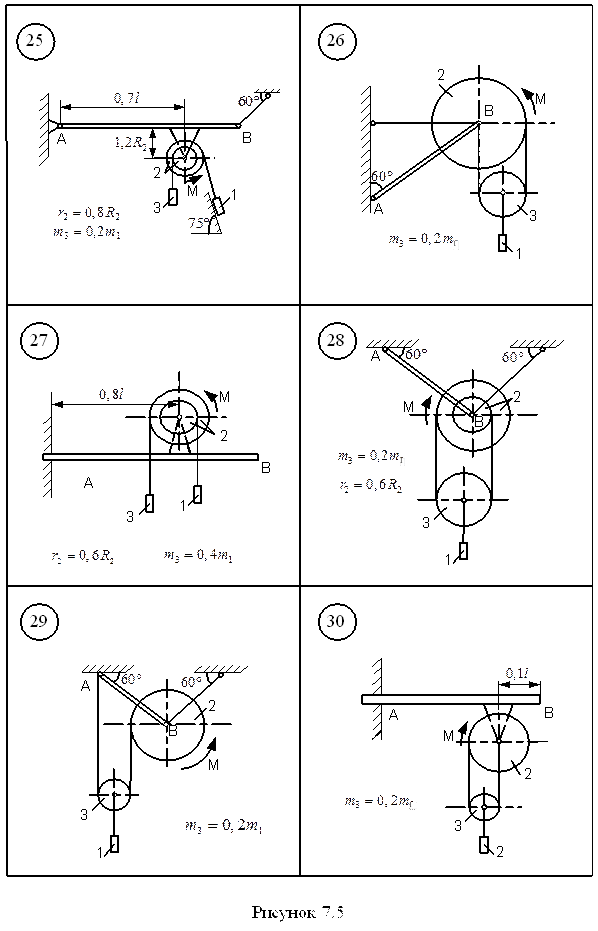
Д.7 Застосування принципу Д’Аламбера для визначення реакції в’язей Для підйому вантажу 1 (рис. 7.1–7.5) використовується електродвигун з моментом М, що приводить до руху барабан 2, маса якого розподілена по ободу радіуса R2 . Знайти реакції в’язей балки АВ вагою P та довжиною l. Масою абсолютно гнучких тросів знехтувати. Ковзання тросів по шківах відсутнє. В схемах 6, 13, 21, 25 похила площина гладенька. Ковзання тіла 1 в точці контакту з похилою площиною (схеми 8, 9, 11, 15, 18, 23, 24) відсутнє. Дані для розрахунку взяти з таблиці 7.1, де прийняті такі позначення: Ір – момент інерції ротора електродвигуна відносно осі обертання; mД – маса електродвигуна; m1 – маса вантажу; mб – маса барабана.
Таблиця 7.1
Приклад виконання завдання
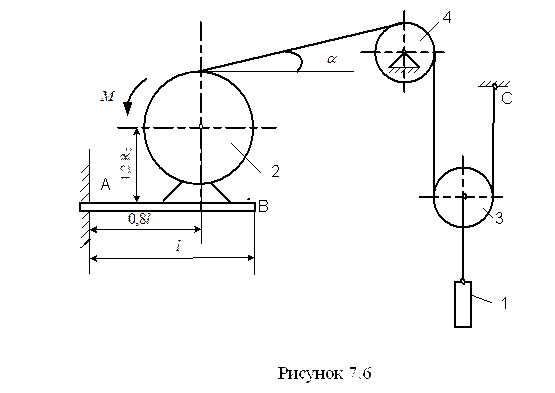
Вантаж 1 (рис. 7.6) тросом з’єднаний з центром мас рухомого блока 3, який приводиться до руху пасом, один кінець якого закріплений в точці С, а другий перекинутий через нерухомий блок 4 і зафіксований на барабані 2 масою m2 , що приводиться до руху електродвигуном з моментом М. Знайти реакції жорсткого защімлення А однорідної балки АВ довжиною l і вагою P. Масою блока 4, троса та паса знехтувати. Маса електродвигуна mД, момент інерції ротора – Ір . Тіло 3 – однорідний диск, а маса барабана 2 розподілена по ободу радіусом R2 . Дані для розрахунку: m1 = 300 кг; Ір = 0,25 кг×м2 ; m3 = 10 кг; m2 = 15 кг; mД = 35 кг; P = 250 Н; l = 1м; R2 = 0,2 м; М = 320 Н×м; a = 30°.
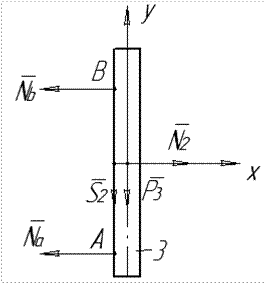
Розв'язування. Розглянемо матеріальну систему, що складається з балки АВ, електродвигуна і барабана 2 (рис 7.7).
Запишемо принцип Д’Аламбера для плоскої довільної системи сил в проекціях на осі Х та Y.
Рівняння (7.1) для системи сил (рис 7.7) записується у вигляді:
де S – реакція паса;
При визначенні моменту сили В трьох рівняннях (7.2) п’ять невідомих
Додаткові рівняння отримаємо, якщо використаємо принцип Д’Аламбера для визначення моментів сил відносно точки К (рис. 7.8) та точки D (рис. 7.9).
(7.3)
де
де xD, yD –реакції балки АВ.
Із рівнянь (7.3), (7.4) визначаємо натяг S паса:
Або, підставляючи дані умови задачі, отримаємо:
Величину сил XA та YA визначаємо з перших двох рівнянь системи (7.2):
Із третього рівняння (7.2) з врахуванням (7.4) визначимо величину МА:
Відповідь: ХА = 931 н, YА = 202,95 н, МА = 87,4 н∙м.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 295; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.15.173 (0.01 с.) |

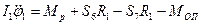 (6.9)
(6.9) відносно осі Z тапари сил з моментом
відносно осі Z тапари сил з моментом  беремо із додатним знаком, а момент сили
беремо із додатним знаком, а момент сили 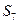 та момент
та момент 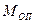 - від’ємним.
- від’ємним. , реакція тіла 1 -
, реакція тіла 1 - 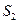 та
та 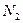 ,реакції S6’, S7’ нескінченного паса, реакція x2, y2 нерухомого шарніра.
,реакції S6’, S7’ нескінченного паса, реакція x2, y2 нерухомого шарніра.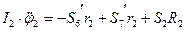 (6.10)
(6.10)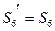 та
та 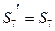 (відповідно до третього закону Ньютона).
(відповідно до третього закону Ньютона).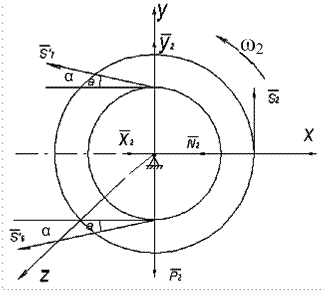
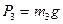 , реакції нерухомих шарнірів
, реакції нерухомих шарнірів 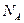 та
та 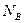 , реакції
, реакції 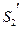 та
та 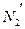 тіла 3, запишемо теорему про рух центра мас в проекціях на вісь Y (вісь Y направляється в сторону руху тіла 3)
тіла 3, запишемо теорему про рух центра мас в проекціях на вісь Y (вісь Y направляється в сторону руху тіла 3)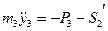 . (6.11)
. (6.11)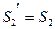 .
.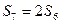 ):
):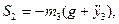
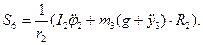
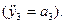

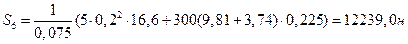
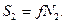
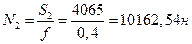
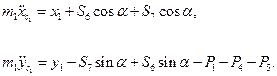 (6.12)
(6.12)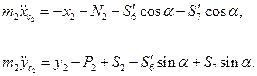 (6.13)
(6.13)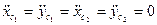 , оскільки центри мас тіл 1,2 знаходяться на нерухомих осях обертання тіл.
, оскільки центри мас тіл 1,2 знаходяться на нерухомих осях обертання тіл.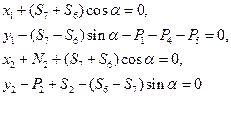 (6.14)
(6.14)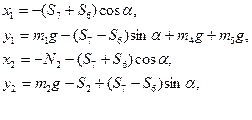
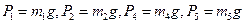
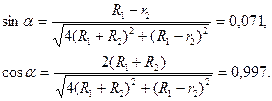
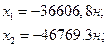
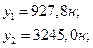
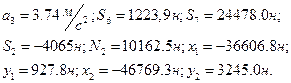

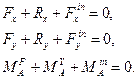 (7.1)
(7.1)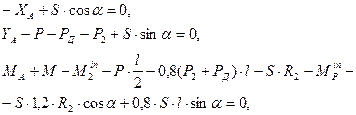 (7.2)
(7.2)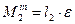 - головний момент сил інерції барабана;
- головний момент сил інерції барабана;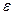 - кутове прискорення ротора електродвигуна та барабана;
- кутове прискорення ротора електродвигуна та барабана; 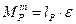 - головний момент сил інерції ротора електродвигуна;
- головний момент сил інерції ротора електродвигуна; 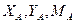 - реакції жорсткого зщімлення;
- реакції жорсткого зщімлення; 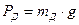 ,
, 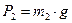 .
.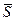 відносно центра А використовувалось правило паралельного переносу сили.
відносно центра А використовувалось правило паралельного переносу сили.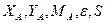 .
.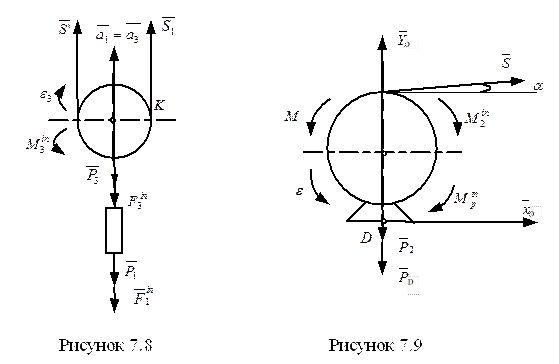
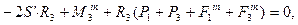
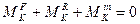 (рис. 7.8),
(рис. 7.8),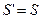 , R3 – радіус шківа 3,
, R3 – радіус шківа 3, 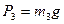 ,
, 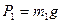 ,
, 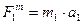 ;
;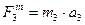 ,
, 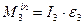 ,
, 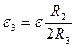 ,
, 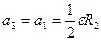 ;
;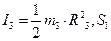 - реакція нерухомої частини троса.
- реакція нерухомої частини троса.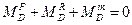 (рис. 7.9),
(рис. 7.9),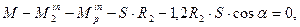 (7.4)
(7.4)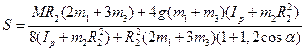 .
.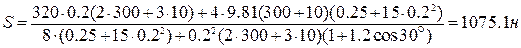 .
.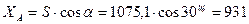 (н).
(н).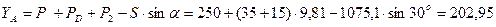 (н).
(н).