
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Д.8 Додаткові динамічні реакції в'язей твердого тіла, що обертається навколо нерухомої осіСодержание книги
Поиск на нашем сайте
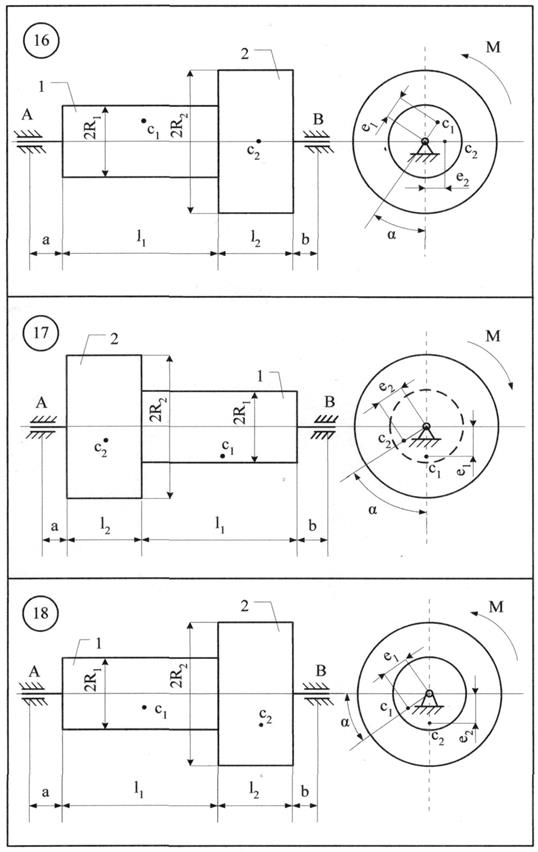
Однорідні тіла 1 та 2 (рис. 8.1 - 8.10) обертаються навколо нерухомої осі z під дією моменту М. Центри мас тіл зміщені від осі обертання (статична неврівноваженість тіл) на величини е1 та е2, відповідно. Знайти додаткові динамічні реакції циліндричних шарнірів А і В при t = t1, і порівняти їх зі статичними, якщо при t = 0 кутова швидкість тіл Дані для розрахунку наведені в табл. 8.1. Якщо
Таблиця 8.1
Приклад виконання завдання До системи однорідних тіл 1 та 2 (рис. 8.11), що обертаються з кутовою швидкістю М = (3+7t) Н · м. Знайти статичні та додаткові динамічні реакції циліндричних шарнірів А і В при t1 = 2с, якщо: m1=3 кг; m2=5 кг; е1=0,1 мм;е2= 0,3 мм; l1= 0,25 м; l2 = 0,25 м; а = 0,05 м; b = 0,15 м; R1=0,1 м; R2=0,2 м.
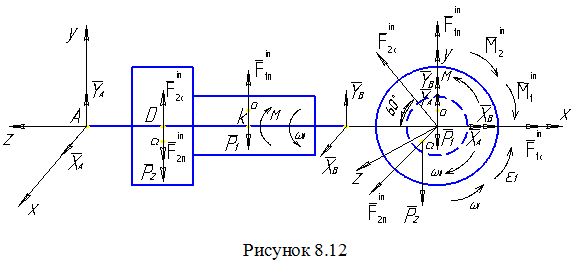
Розв'язання. Переміщенню тіл 1 та 2 (рис 8.11) перешкоджають в'язі: нерухомі (циліндричні) шарніри А і В. На підставі аксіоми звільнення від в'язей, дію шарнірів А і В та тіла замінюємо реакціями в'язей – YA, XA, YB, XB (рис. 8.12).
Рисунок 8.1
Рисунок 8.2
Рисунок 8.3
Рисунок 8.4
Рисунок 8.5
Рисунок 8.6
Рисунок 8.7
Рисунок 8.8
Рисунок 8.9
Рисунок 8.10
Рисунок 8.11
Реакції YA, XA, YB, XB запишемо як суму статичних YAC, XAC, YBC, XBC та додаткових динамічних реакцій YA∆, XA∆, YB∆, XB∆. YA = YAC + YA∆, XA = XAC + XA∆, (8.1)
Статичні реакції в'язей визначаються при
де Розв’язуючи систему рівнянь, маємо:
Таким чином: RAC = 54,85 Н, RBC = 23,63 Н.
Для визначення реакцій циліндричних шарнірів А і В (рис.8.12), використаємо принцип Д’Аламбера:
В проекціях на осі X, Y, Z
де сили інерції, зведені до центрів D і K;
де ε – кутове прискорення; ω – кутова швидкість тіл;
Із останнього рівняння системи (8.3) знайдемо кутову швидкість ω та кутове прискорення ε тіл.
де
Оскільки
Інтегруємо диференціальне рівняння (8.4) при початкових умовах: при t1= 0,
Звідки: Визначимо кутове прискорення
де Додаткові динамічні реакції опор А і В знайдемо із перших чотирьох рівнянь системи (8.3), враховуючи (8.1) та (8.2)
де Або:
Із рівнянь (8.6) знаходимо складові додаткових динамічних реакцій циліндричних шарнірів:
Додаткові динамічні реакції циліндричних шарнірів А і В
При Відповідь: R∆A = 31,94 н, R∆В = 7,95 н. Принцип Лагранжа Д. 9 Визначення реакцій в’язей врівноваженого плоского механізму за допомогою принципу віртуальних переміщень
Плоский механізм, що зображений на рисунках 9.1 – 9.5 в тридцяти варіантах, знаходиться в рівновазі під дією сил
Таблиця 9.1
Застосовуючи принцип віртуальних переміщень, визначити силу
Приклад виконання завдання Плоский механізм, що зображений на рисунку 9.6, знаходиться в рівновазі під дією сил Розв’язання. Застосовуємо принцип віртуальних переміщень.
Надаємо точкам механізму можливі переміщення, які не порушують умов ідеальних в’язей. Якщо стержень ОВ повернеться навколо осі О на малий кут
Рисунок 9.1
Рисунок 9.3
Рисунок 9.6 Рисунок 9.7
Згідно з принципом (9.1) запишемо суму віртуальних робіт для силових навантажень M, P і F.
Встановимо залежність між переміщеннями і виразимо Для ланки ОВ: Для ланки АD на основі того, що проекції переміщень на вісь, що проходить через точки А і D, буде: Тому:
Підставляємо переміщення (9.3) в рівняння (9.2)
Переміщення
Підставляємо дані:
Відповідь: F = 0,61 кН.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.31.48 (0.011 с.) |

 .
. , град
, град
 , c-1
, c-1










 YB = YBC + YB∆, XB = XBC + XB∆.
YB = YBC + YB∆, XB = XBC + XB∆. = 0,
= 0, 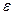 = 0 з рівнянь (рис.8.12):
= 0 з рівнянь (рис.8.12):


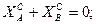

 (8.2)
(8.2)






 .
.


 (8.3)
(8.3)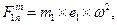



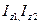 - моменти інерції тіл відносно осі Z; M=(3+7t)
- моменти інерції тіл відносно осі Z; M=(3+7t) ,
, .
. , тоді
, тоді . (8.4)
. (8.4)

 (8.5)
(8.5)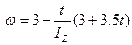 .
. (8.4) та кутову швидкість (8.5) при t1 = 2 c.
(8.4) та кутову швидкість (8.5) при t1 = 2 c.
 .
.

 (8.6)
(8.6) 
 , при
, при 


 додаткові динамічні реакції шарнірів складають 59% для шарніра А та 33,6% для шарніра В від статичних реакцій в’язей.
додаткові динамічні реакції шарнірів складають 59% для шарніра А та 33,6% для шарніра В від статичних реакцій в’язей. і моменту
і моменту  . Розміри ланок, кути, значення
. Розміри ланок, кути, значення  і
і 
 , якщо ланки механізму є ідеальними твердими тілами, а тертя відсутнє.
, якщо ланки механізму є ідеальними твердими тілами, а тертя відсутнє. перпендикулярна до горизонтальної лінії ОД. В остаточних розрахунках прийняти, що
перпендикулярна до горизонтальної лінії ОД. В остаточних розрахунках прийняти, що  м,
м,  м,
м,  кН
кН  м,
м,  кН,
кН, 
 . (9.1)
. (9.1) , то точки А і В набувають лінійних переміщень
, то точки А і В набувають лінійних переміщень  і
і  , відповідно. Переміщення зображаємо на рис. 9.7. Можливе переміщення для точки D -
, відповідно. Переміщення зображаємо на рис. 9.7. Можливе переміщення для точки D -  .
.
 Рисунок 9.2
Рисунок 9.2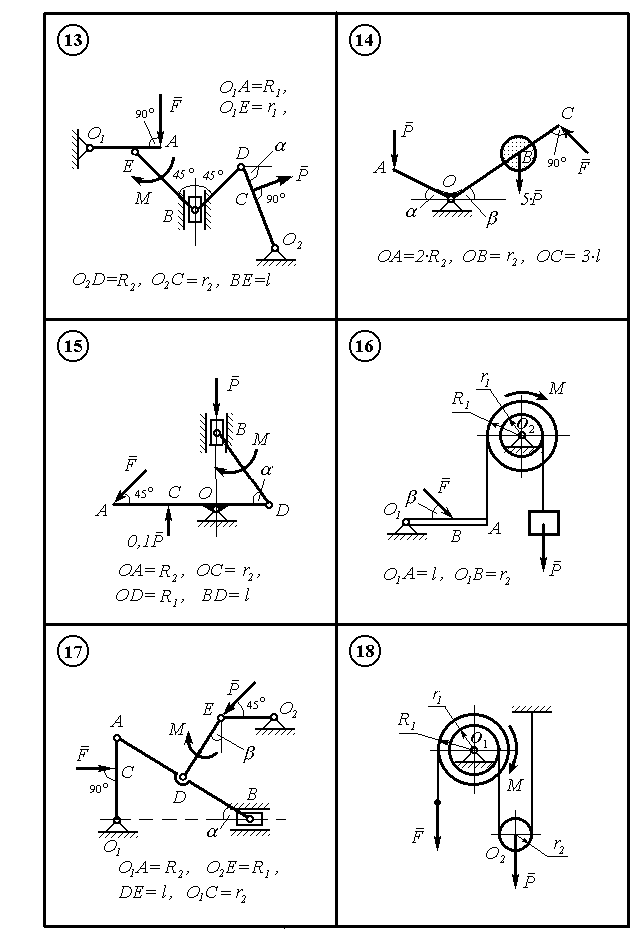
 Рисунок 9.4
Рисунок 9.4 Рисунок 9.5
Рисунок 9.5
 . (9.2)
. (9.2) .
. .
. . (9.3)
. (9.3) .
. , тому після скорочення на
, тому після скорочення на  . (9.4)
. (9.4)



