
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Видмиш А. А., Приятельчук В. О., Федотов В. О.Содержание книги
Поиск на нашем сайте
Теоретична механіка. Динаміка. Розрахунково-графічні та контрольні завдання. Навчальний посібник. – Вінниця: ВНТУ, 2008. -143с. Збірник уміщує 13 завдань із динаміки точки, твердого тіла, матеріальної системи. Кожне завдання має триста варіантів з прикладом виконання. Для студентів денної та заочної форм навчання.
УДК 531(075)
© А. А. Видмиш, В. О. Приятельчук, В. О. Федотов, 2009 Зміст Порядок та основні вимоги до виконання роботи.................................... 5 Розрахунково-графічні та контрольні завдання....................................... 6 ............................................... Динаміка точки……………………………... 6 Д.1 Дослідження руху точки.............................................................. 6 1.1 Приклад виконання завдання........................................................... 10 Динаміка системи…………………………..15 Д.2 Використання теореми про рух центра мас для визначення переміщення тіл........................................................................................ 15 2.1 Приклад виконання завдання........................................................... 21 Д.3 Використання теореми про зміну головного вектора кількості руху системи для дослідження переміщення тіл..................................... 23 3.1 Приклад виконання завдання........................................................... 34 Д.4 Використання теореми про зміну кінетичного моменту для дослідження руху матеріальної системи................................................. 38 4.1 Приклад виконання завдання........................................................... 44 Д.5 Використання теореми про зміну кінетичної енергії для вивчення руху матеріальної системи....................................................... 49 5.1 Приклад виконання завдання............................................................ 55 Д.6 Дослідження руху матеріальної системи із застосуванням основних (загальних) теорем динаміки................................................... 60 6.1 Приклад виконання завдання........................................................... 60 6.1.1 Визначення зусиль в пасах та між тілами..................................... 74 6.1.2 Визначення реакцій циліндричних шарнірів................................ 76 Принцип Д’Аламбера………………….......78 Д.7 Застосування принципу Д’Аламбера для визначення реакції в’язей........................................................................................................ 78 7.1 Приклад виконання завдання........................................................... 84 Д.8 Додаткові динамічні реакції в’язей твердого тіла, що обертається навколо нерухомої осі......................................................... 88 8.1 Приклад виконання завдання........................................................... 88 Принцип Лагранжа……………………….102 Д.9 Визначення реакцій в’язей врівноваженого плоского механізму за допомогою принципу віртуальних переміщень............. 102 9.1 Приклад виконання завдання......................................................... 102 Д.10 Визначення опорних реакцій для складної статичної конструкції за допомогою принципу віртуальних переміщень........... 110 10.1 Приклад виконання завдання....................................................... 110 Загальне рівняння динаміки.......................122 Д.11 Розрахунок характеристик руху механічної системи за допомогою загального рівняння динаміки........................................... 122 11.1 Приклад виконання завдання....................................................... 122
Рівняння Лагранжа 2-го роду…………….132 Д.12 Дослідження руху матеріальної системи з використанням рівняння Лагранжа 2-го роду................................................................ 132 12.1 Приклад виконання завдання....................................................... 132 Д.13 Дослідження вільних коливань матеріальної системи............ 135 13.1 Приклад виконання завдання....................................................... 135 Література........................................................................................... 142
Порядок та основні вимоги до виконання роботи З розділу „Динаміка” студенти виконують одну розрахунково-графічну або контрольну роботу. Студенти вибирають варіант схеми (рисунки) за двома останніми цифрами (шифр) залікової книжки (за винятком завдання Д.1) з таблиці 1, а дані для розрахунку – за останньою цифрою шифру з таблиць, що наведені в завданнях. В завданні Д.1 за останньою цифрою шифру вибирається схема, а за двома останніми – дані для розрахунку.
Таблиця 1
Студенти денної форми навчання оформляють розрахунково-графічне завдання відповідно до діючих стандартів ЄСКД (ГОСТ 2.105-95 або ДСТУ 3008-95). Студенти заочної форми навчання можуть виконувати завдання в зошитах. На титульні сторінці зошита вказується номер контрольної роботи, назва дисципліни, прізвище та ініціали студента, шифр, факультет, група і домашня адреса. Розв’язання кожної задачі потрібно починати на розвороті зошита (з лівої сторінки), так, щоб розрахункова схема та формули, складені за нею, знаходились поряд. На початку сторінки пишеться номер завдання, варіант і наводиться коротка умова задачі (що відомо та що потрібно знайти). Розрахункові схеми (рисунки) виконуються за допомогою креслярських приладів. Розрахунки необхідно супроводжувати короткими поясненнями. На кожній сторінці залишають поля для зауважень рецензента. Якщо робота висилається на повторну перевірку (при виконанні її у другому зошиті) обов’язково прикладається незарахована робота. Після зарахування усіх задач студент повинен до іспиту захистити роботу. Графік захисту планується деканом.
Розрахунково-графічні та контрольні завдання Динаміка точки Д.1 Дослідження руху точки Невільна матеріальна точка масою m (рис.1.1) рухається протягом τ с. по шорсткій поверхні ОА (коефіцієнт тертя ковзання f). В пункті А матеріальна точка із швидкістю Якщо точка рухається під дією постійних сил (табл.1.1), прийняти (рис.1.1), що сила
Рисунок 1.1
Рисунок 1.1 (продовження)
Таблиця 1.1
Таблиця 1.2
Приклад виконання завдання На невільну матеріальну точку масою m, що рухається по похилій шорсткій поверхні ОА (рис. 1.2), діє сила
Рисунок 1.2
Знайти і побудувати траєкторію руху точки на ділянці АВ, її швидкість в пункті В якщо: коефіцієнт тертя ковзання – f = 0,25; початкова швидкість точки v0 = 0,5 м/c; τ = 2 с; d = 2,0 м. Розв’язання. Точка масою m на ділянці ОА переміщується під дією сил: ваги Запишемо закон руху точки на ділянці ОА
в проекціях на осі Х1 та У1.
Рисунок 1.3
Силу тертя знайдемо за законом Амонтона-Кулона, який при переміщені точки з невеликою швидкістю запишеться:
Оскільки точка рухається по прямій ОА, тоді
де Диференціальне рівняння (1.1), враховуючи (1.3) та (1.4) і значення сили F, набуває вигляду:
Або
Інтегруємо диференціальне рівняння (1.5) при початкових умовах: при,
Відстань ОА точка проходить за τ с і її швидкість vA в точці А знаходимо за формулою (1.6) при t1= τ
На ділянці АВ (рис. 1.4) точка рухається під дією сили ваги
Рисунок 1.4
Запишемо диференціальне рівняння руху точки в проекціях на осі Х та У.
де Тоді
Або
При t =0; Оскільки
Інтегруючи рівняння при початкових умовах (1.11), знаходимо:
Або
Інтегруємо рівняння (2.12) та (2.13) при початкових умовах (1.11).
Або
Із рівняння (1.14) та (1.15) знаходимо рівняння траєкторії руху точки на ділянці АВ.
Будуємо траєкторію руху точки (рис.1.5,б), використовуючи рівняння(1.16) (рис. 1.5,а) або формули (1.14) та (1.15).
а) б) Рисунок 1.5
Знайдемо швидкість точки vB. При t2=T, xT=d; тоді із рівняння (1.14) визначаємо час Т руху точки на ділянці АВ.
На підставі рівняння (1.12) та (1.13) визначаємо проекції швидкості
Швидкість точки
На ділянці АВ швидкість точки зменшилась від vA =42,06 м/с до vВ =0,82 м/с,тобто в
Відповідь: Динаміка системи
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.93.61 (0.01 с.) |

 залишає поверхню ОА і через Тс падає в точку В ділянки АВ із швидкістю
залишає поверхню ОА і через Тс падає в точку В ділянки АВ із швидкістю 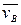 . Знайти і побудувати траєкторію руху точки на ділянці АВ та її швидкість в точці В.
. Знайти і побудувати траєкторію руху точки на ділянці АВ та її швидкість в точці В.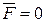 , а при змінних силах (табл. 1.2) сила опору
, а при змінних силах (табл. 1.2) сила опору 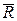 руху точки на ділянці АВ має напрямок протилежний вектору швидкості
руху точки на ділянці АВ має напрямок протилежний вектору швидкості  точки.
точки.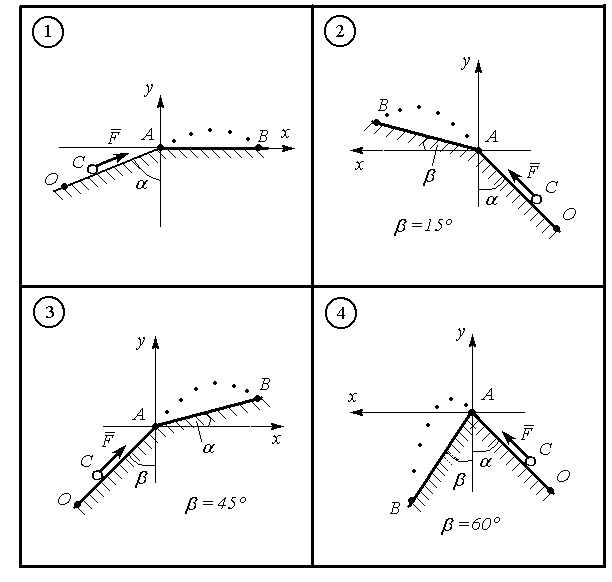

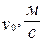
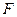 , H
, H

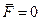
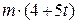


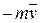

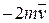
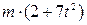

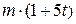
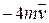

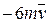

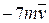
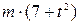
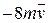



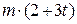



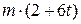
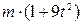

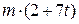



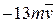
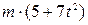

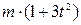
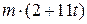
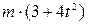
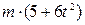
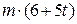

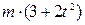
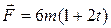 H. Із швидкістю
H. Із швидкістю  Н.
Н.
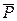 , сили
, сили 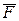 , нормальної реакції
, нормальної реакції 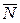 шорсткої поверхні та сили тертя
шорсткої поверхні та сили тертя 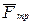 (рис. 1.3).
(рис. 1.3).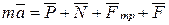
 . (1.1)
. (1.1)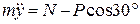 . (1.2)
. (1.2)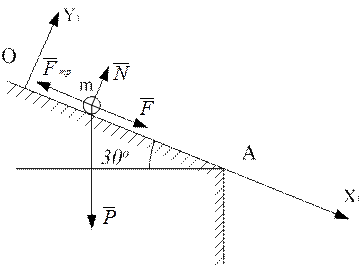
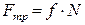 . (1.3)
. (1.3)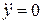 , і з рівняння (1.2) отримаємо:
, і з рівняння (1.2) отримаємо: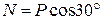 , (1.4)
, (1.4) .
.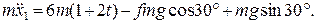
 (1.5)
(1.5)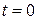 ,
, 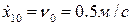 .
.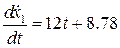 ,
, ,
,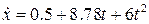 . (1.6)
. (1.6) ,
,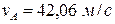 .
.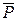 та сили опору
та сили опору  , що направлена в протилежну сторону швидкості точки.
, що направлена в протилежну сторону швидкості точки.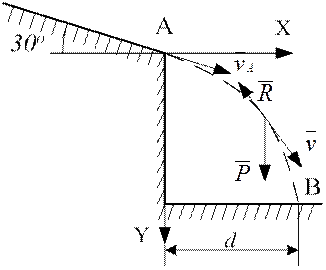
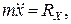 (1.7)
(1.7) . (1.8)
. (1.8)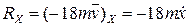 ,
, 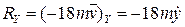 ,
,  .
. .
.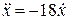 . (1.9)
. (1.9) . (1.10)
. (1.10)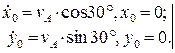 (1.11)
(1.11)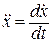 ,
, 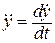 , то в диференціальних рівняннях (1.9) та (1.10), розподіляючи, змінні, отримаємо:
, то в диференціальних рівняннях (1.9) та (1.10), розподіляючи, змінні, отримаємо: ,
,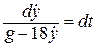 .
.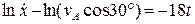 ,
, 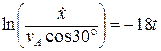 .
.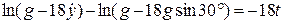 ,
,  .
.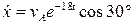 . (1.12)
. (1.12) . (1.13)
. (1.13)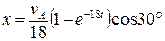 .
.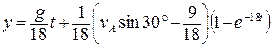 .
. . (1.14)
. (1.14) . (1.15)
. (1.15)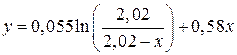 . (1.16)
. (1.16)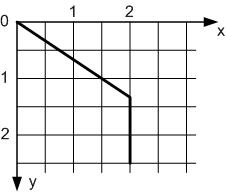
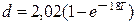 ,
, .
. по осі Х та У (t2=T)
по осі Х та У (t2=T)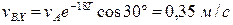 .
.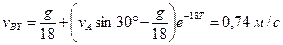 .
. ,
, .
.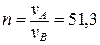 раза за рахунок сили
раза за рахунок сили 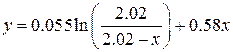 ,
, 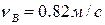 .
.


