Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальне рівняння (5.1), враховуючи (5.2) набуває виглядуСодержание книги
Поиск на нашем сайте
Знайдемо кінематичні співвідношення між швидкостями точок, кутовими швидкостями тіл, записавши їх через швидкість V1 центра мас тіла1. Кутова швидкість тіла 1, враховуючи, що миттєвий центр швидкості тіла 1 знаходиться в точці О1 (рис.5.6) ω 1= де R1 – радіус однорідного суцільного диска (тіла) 1. Кутова швидкість тіла 2
Швидкість точки А, враховуючи, що тіла 2 та 3 з’єднані нерозтяжним шнуром.
Оскільки точка О3 – миттєвий центр швидкості тіла 3, тоді
Із (5.6) та (5.7) визначаємо кутову швидкість тіла 3
Швидкість V3 центра мас тіла 3
Знайдемо переміщення центра мас тіла 3. Оскільки
i, враховуючи (5.9), отримаємо
або
При t = 0, S1 = 0, та S3 = 0 і після інтегрування (5.11) маємо:
Знайдемо кінетичну енергію матеріальної системи як суму кінетичних енергій тіл 1,2 та 3. Т=Т1+Т2+Т3. (5.13)
де
Тіло 2 обертається навколо горизонтальної осі і кінетична енергія знаходиться за формулою
де І2 = ω 2 − кутова швидкість тіла 2 (5.5). Тоді
Кінетична енергія тіла 3
де І3 =
Тепер кінетичну енергію (5.13) системи, враховуючи (5.14) – (5.16), визначимо за формулою
Покажемо зовнішні сили, що прикладені до матеріальної системи (рис.5.6). Знайдемо суму потужностей зовнішніх сил. Потужність сил Потужність сил Потужність зовнішніх сил, під дією яких рухається матеріальна система (рис. 5.6)
де
Тоді, враховуючи що (5.9)
отримаємо
Підставляючи (5.17) і (5.18) в (5.3), маємо
Оскільки
Або, підставляючи дані умови задачі,
Знайдемо швидкість центра мас тіла 1. Рівняння (5.19) запишемо у вигляді:
При t=0, V10=0, S10=0. При t=t, V1t=V1, S1t=S1 , (5.21)
де t - час, за який центр мас тіла 1 пройде шлях S1. Інтегруючи рівняння (5.20) за умовами (5.21), визначаємо швидкість центра мас тіла 1 за час t (
або підставляючи числові дані, отримаємо:
Відповідь:
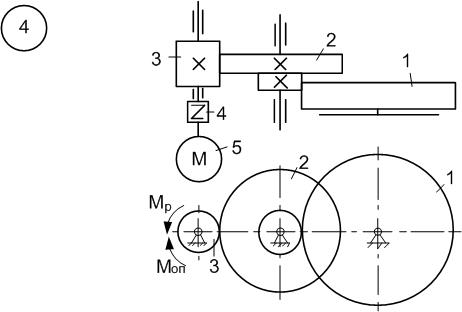
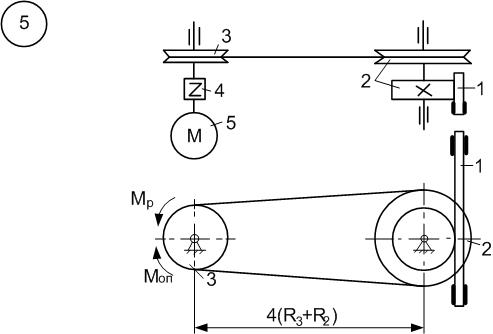
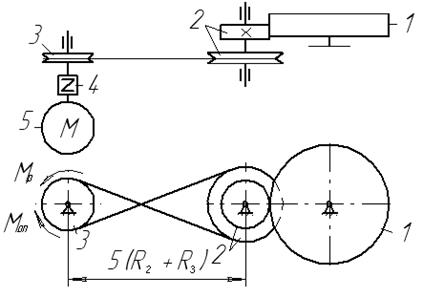
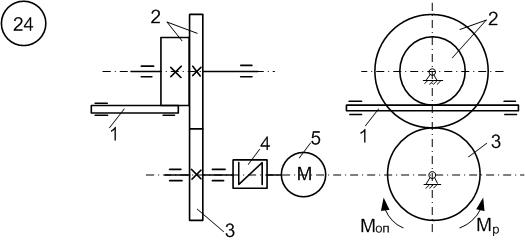
Д.6 Дослідження руху матеріальної системи з застосуванням основних (загальних) теорем динаміки Матеріальна система (рис.6.1-6.10) приводиться до руху електродвигуном 5, момент якого в період пуску Знайти прискорення (схеми 1-3, 5-10, 12-17, 19-30) або кутове прискорення (схеми 4,11,18) тіла 1, зусилля в пасах та між тілами, реакції циліндричних шарнірів тіл 2 і 3 в момент часу Натяг у ведучій частині нескінченного паса (схеми 5,10-13,16,18,22, 25,27,28,30) вдвічі більший від натягу у веденій. Однорідне тіло 3 та східчастий шків 2 обертаються навколо паралельних осей. В точках контакту тіл ковзання відсутнє. Коефіцієнт тертя ковзання між тілами дорівнює f. Тіло 1 (схеми 2,10,19,30) переміщується по гладенькій похилій площині. Масами пасів та їх ковзанням по шківах знехтувати. Дані для розрахунку взяти з таблиці 6.1, де прийняті такі позначення:
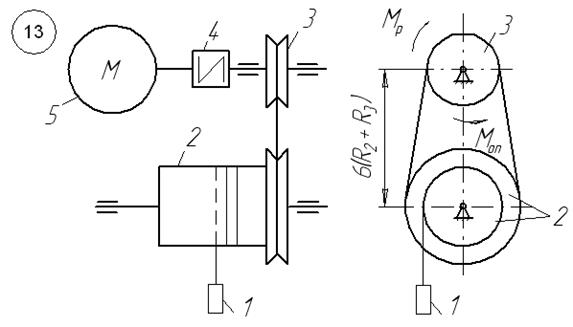
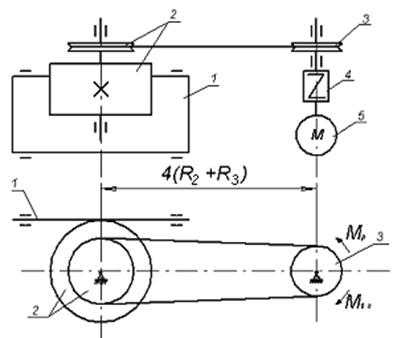
Приклад виконання завдання Матеріальна система (рис. 6.11) починає рухатись із стану спокою під дією моменту Визначити при Прийняти: Розв’язання. Для визначення прискорення тіла 3 (рис. 6.12) використаємо теорему про зміну кінетичної енергії в диференціальній формі.
Рисунок 6.1
Рисунок 6.2
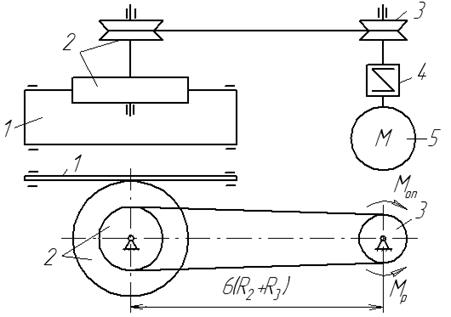
Рисунок 6.3
Рисунок 6.4
Рисунок 6.5
Рисунок 6.6
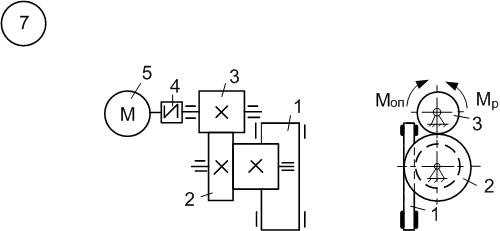
Рисунок 6.7
Рисунок 6.8
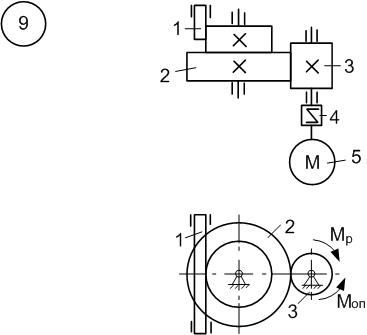
Рисунок 6.9
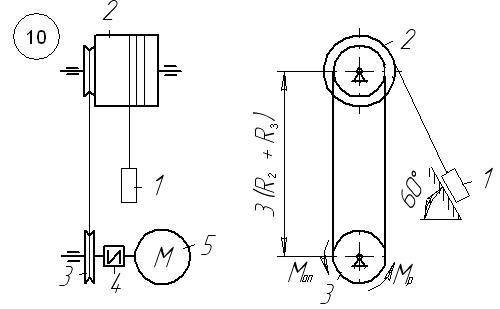
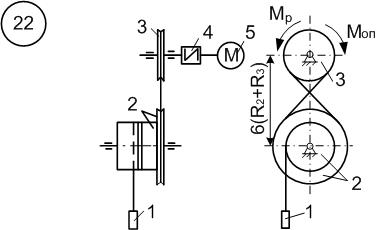
Рисунок 6.10
Рисунок 6.11
де Т – кінетична енергія системи;
Кінетична енергія системи складається із кінетичної енергії тіл, що входять в систему
Тіла 1,2,4 та 5 обертаються навколо нерухомих горизонтальних осей і їх кінетична енергія знаходиться за формулами:
де
Взаємозв’язок між кінетичними характеристиками руху тіл (рис. 6.12)
Тіло 3 переміщується поступально із швидкістю Запишемо кінетичну енергію системи, враховуючи (6.2), (6.3) та (6.4) як функцію швидкості
де
Рисунок 6.12
Знайдемо суму потужності зовнішніх сил (рис. 6.12) матеріальної системи: сили тяжіння Потужність сил P1, P2, P3, P4, x1, y1, x2, y2, NA і NB дорівнює нулю тому, що точки прикладання сил не переміщуються. Тоді
де
Або
Теорема про зміну кінетичної енергії матеріальної системи (6.1) з врахуванням (6.5) та (6.6) запишеться:
Оскільки
Підставляючи дані умови задачі, отримаємо:
При t1 =1.5 c, a3 =3,74 м/с2. Кутові прискорення тіл 1 та 2
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.153.218 (0.009 с.) |

 =∑ Nе. (5.3)
=∑ Nе. (5.3)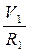 , (5.4)
, (5.4) (5.5)
(5.5) . (5.6)
. (5.6) . (5.7)
. (5.7)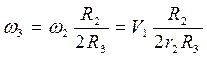 . (5.8)
. (5.8) . (5.9)
. (5.9)
 (5.10)
(5.10)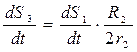
 . (5.11)
. (5.11) . (5.12)
. (5.12)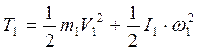 ,
, − момент інерції тіла 1 відносно центральної осі. Тоді, враховуючи (5.4),
− момент інерції тіла 1 відносно центральної осі. Тоді, враховуючи (5.4),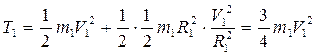 . (5.14)
. (5.14)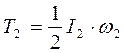
 − момент інерції тіла 3 відносно головної центральної осі;
− момент інерції тіла 3 відносно головної центральної осі; . (5.15)
. (5.15) ,
, − момент інерції тіла 3 відносно головної центральної осі;
− момент інерції тіла 3 відносно головної центральної осі; - (5.8);
- (5.8);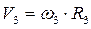 − швидкість центра мас тіла 3.
− швидкість центра мас тіла 3. . (5.16)
. (5.16)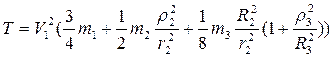 . (5.17)
. (5.17) ,
,  ,
, 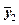 дорівнює нулю тому, що точка О2 прикладення сил нерухома.
дорівнює нулю тому, що точка О2 прикладення сил нерухома.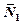 ,
,  ,
,  ,
,  , дорівнює нулю, оскільки сили прикладені в миттєвих центрах швидкостей тіла 1 та 3.
, дорівнює нулю, оскільки сили прикладені в миттєвих центрах швидкостей тіла 1 та 3. ,
,


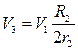
 (5.18)
(5.18) (5.19)
(5.19) (а1 – прискорення центра мас тіла 1), тоді
(а1 – прискорення центра мас тіла 1), тоді .
.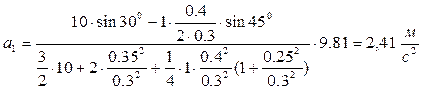 .
. (5.20)
(5.20)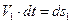 ).
).
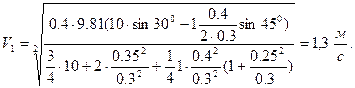
 ;
;  .
. .
. якщо момент опору руху
якщо момент опору руху  .
.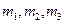 - маса тіл 1,2 та 3;
- маса тіл 1,2 та 3; 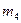 - маса пружної муфти;
- маса пружної муфти;  - маса ротора електродвигуна;
- маса ротора електродвигуна;  - моменти інерції пружної муфти 4 та ротора електродвигуна 5 відносно осі обертання;
- моменти інерції пружної муфти 4 та ротора електродвигуна 5 відносно осі обертання;  - розміри тіл 3 та 2;
- розміри тіл 3 та 2;  - радіус інерції тіла 2.
- радіус інерції тіла 2. електродвигуна 5. Осі тіл 1 та 2 горизонтальні. Коефіцієнт тертя між тілами f. В точках контакту тіл ковзання відсутнє. Масою паса знехтувати.
електродвигуна 5. Осі тіл 1 та 2 горизонтальні. Коефіцієнт тертя між тілами f. В точках контакту тіл ковзання відсутнє. Масою паса знехтувати. прискорення тіла 3, натяг
прискорення тіла 3, натяг  у веденій 6 та ведучій 7 (
у веденій 6 та ведучій 7 (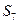 ) частині паса (
) частині паса (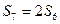 ), зусилля в точці контакту тіл 2 та 3, реакції в’язей циліндричних (нерухомих) шарнірів тіл 1 та 2 якщо момент опору
), зусилля в точці контакту тіл 2 та 3, реакції в’язей циліндричних (нерухомих) шарнірів тіл 1 та 2 якщо момент опору  м;
м;  м;
м;  м;
м;  м;
м; 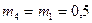 кг;
кг; 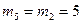 кг;
кг; 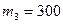 кг;
кг; 

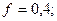
































 (6.1)
(6.1) - сума потужності зовнішніх сил системи;
- сума потужності зовнішніх сил системи; - сума потужності внутрішніх сил системи;
- сума потужності внутрішніх сил системи;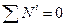 - тіла тверді, а пас абсолютно гнучкий та нерозтяжний.
- тіла тверді, а пас абсолютно гнучкий та нерозтяжний.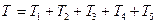 .
.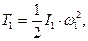
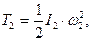
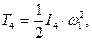
 (6.2)
(6.2)
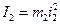 - моменти інерції відповідно тіл 1 та 2;
- моменти інерції відповідно тіл 1 та 2; - кутові швидкості тіл.
- кутові швидкості тіл.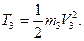 (6.3)
(6.3)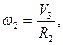
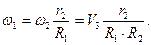 (6.4)
(6.4)
 , тоді
, тоді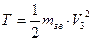 (6.5)
(6.5) зведена маса системи.
зведена маса системи.
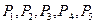 , моменту електродвигуна
, моменту електродвигуна 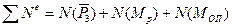 ,
,
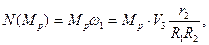
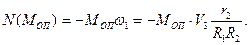
 (6.6)
(6.6) . (6.7)
. (6.7) тоді
тоді . (6.8)
. (6.8)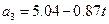 .
.