
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Д.11 Розрахунок характеристик руху механічної системи за допомогою загального рівняння динамікиСодержание книги
Поиск на нашем сайте
Механічна система (рис. 11.1 – 11.5) складається з вантажу 1 масою Визначити прискорення вантажу 1 і натяг троса, який до нього закріплений, якщо масою тросів і тертям в підшипниках шківів нехтуємо. В остаточних розрахунках прийняти значення параметрів з таблиці 11.1 по варіантах.
Таблиця 11.1
Приклад виконання завдання
Для механічної системи, яка наведена на рис. 11.6, задано: Визначити прискорення тіла 1 –
Рисунок 11.1
Рисунок 11.3
Рисунок 11.4
Рисунок 11.6 Розв’язання. Для розв’язування задачі використовуємо загальне рівняння динаміки:
Покажемо для всіх тіл механізму активні сили, напрямки прискорень, інерційні сили і віртуальні переміщення, що зображені на рис. 11.7.
Рисунок 11.7
Активні сили: Інерційні сили: Віртуальні переміщення: для тіла 1 – Складаємо загальне рівняння динаміки відповідно до формули (11.1).
В рівняння (11.2) не ввійшли сили
Звідки:
Моменти інерції тіл 2 і 4 відповідно рівні:
Знайдемо активні сили:
Знайдемо інерційні сили:
Виразимо кутові прискорення
тому Тоді інерційні сили матимуть вигляд:
Підставляємо активні сили (11.5), інерційні сили (11.6) і віртуальні переміщення (11.3) в рівняння (11.2)
Після спрощення і скорочення на
звідки
Підставимо дані умови:
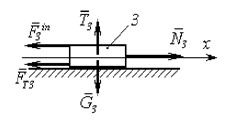
Для визначення натягів тросів, що прикріплені до тіл 1 і 3, застосовуємо принцип Даламбера. Розглянемо сили, які діють на вантаж 1 і покажемо їх на рис. 11.8.
Проектуємо цю векторну рівність на вісь oy, отримаємо:
Звідки
Або:
Рисунок 11.8
Розглянемо сили, які діють на тіло 3, що зображено на рис. 11.9., на основі
Проектуємо це рівняння на вісь ox.
Рисунок 11.9
Звідки:
Відповідь: a1=8.43 м/с2, N3=26.4 н. Рівняння Лагранжа 2-го роду Д. 12 Дослідження руху матеріальної системи з використанням рівняння Лагранжа 2-го роду Матеріальна систем (рис. 11.1 – 11.5) починає рухатись із стану спокою. Знайти прискорення та швидкість з якою опускається тіло1 1після того, коли воно пройде шлях S. Масами шнурів, силами опору знехтувати. Тіла котяться по поверхні без ковзання. Величини для розрахунків взяти з табл. 11.1 (С.123).
Приклад виконання завдання Знайти прискорення та швидкість центра мас тіла 1 (рис. 12.1), коли він пройде відстань S1, якщо матеріальна система починає рухатися із стану спокою. Масою тросів знехтувати. Тіла 1 та 3 переміщуються без ковзання. Прийняти: m1 = 10 кг; m2 = 2 кг; m3 = 1 кг; R2 = 0,4 м; r2 = 0,3 м; r3 = 0,2 м; ρ2 = 0,3 м; ρ3 = 0,25; α = 300; β = 450; S1 = 0,4 м.
Рисунок 12.1
Розв’язання. Положення тіл системи (рис. 12.1) визначаємо узагальненою координатою х. Для дослідження руху матеріальної системи застосуємо рівняння Лагранжа 2- го роду
На рис. 12.1
де Знайдемо ліву частину рівняння (12.1)
де Узагальнену силу Qx знайдемо за формулою
де
Робота сил Віртуальна робота активних сил
де Тепер Тоді з формули (12.5), враховуючи (12.7), отримаємо:
Рівняння Лагранжа 2-го роду (12.1) при врахуванні (12.3), (12.4) і (12.8) набуває вигляду:
звідки:
Або, підставляючи дані з умови задачі,
Оскільки
Підставляючи числові дані, отримаємо:
Відповідь: a1=2.41 м/с2, v1=1.3 м/с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.176.109 (0.009 с.) |

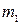 , двох шківів 2 і 3 з масами
, двох шківів 2 і 3 з масами 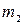 і
і  , радіусами ступенів
, радіусами ступенів 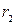 і
і  ,
, 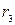 і
і 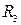 , та радіусами інерції
, та радіусами інерції 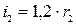 ,
,  відповідно і суцільного циліндри-чного катка 4 масою
відповідно і суцільного циліндри-чного катка 4 масою 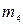 . На шків 2 або 3, діє постійний момент М. Вантаж 1, або каток 4, лежать на гладенькій горизонтальній або похилій площині з кутом нахилу
. На шків 2 або 3, діє постійний момент М. Вантаж 1, або каток 4, лежать на гладенькій горизонтальній або похилій площині з кутом нахилу 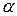 чи
чи  до горизонталі. Тертя при русі вантажу 1 і ковзання при кочені катка 4 відсутні.Система розташована в вертикальній площині.
до горизонталі. Тертя при русі вантажу 1 і ковзання при кочені катка 4 відсутні.Система розташована в вертикальній площині.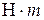
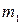


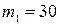 кг,
кг,  кг,
кг,  кг,
кг,  кг,
кг, 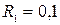 м,
м, 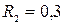 м,
м,  м,
м, 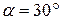 . Радіус інерції ступінчатого барабана 2 рівний
. Радіус інерції ступінчатого барабана 2 рівний 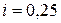 м, коефіцієнт тертя ковзання тіла 3 по горизонтальній площині
м, коефіцієнт тертя ковзання тіла 3 по горизонтальній площині 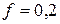 . Циліндричне тіло 4 котиться по похилій площині без тертя і без ковзання.
. Циліндричне тіло 4 котиться по похилій площині без тертя і без ковзання. , тіла 3 –
, тіла 3 – 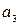 , натяги тросів N1 і N3, до яких ці тіла прикріплені.
, натяги тросів N1 і N3, до яких ці тіла прикріплені.
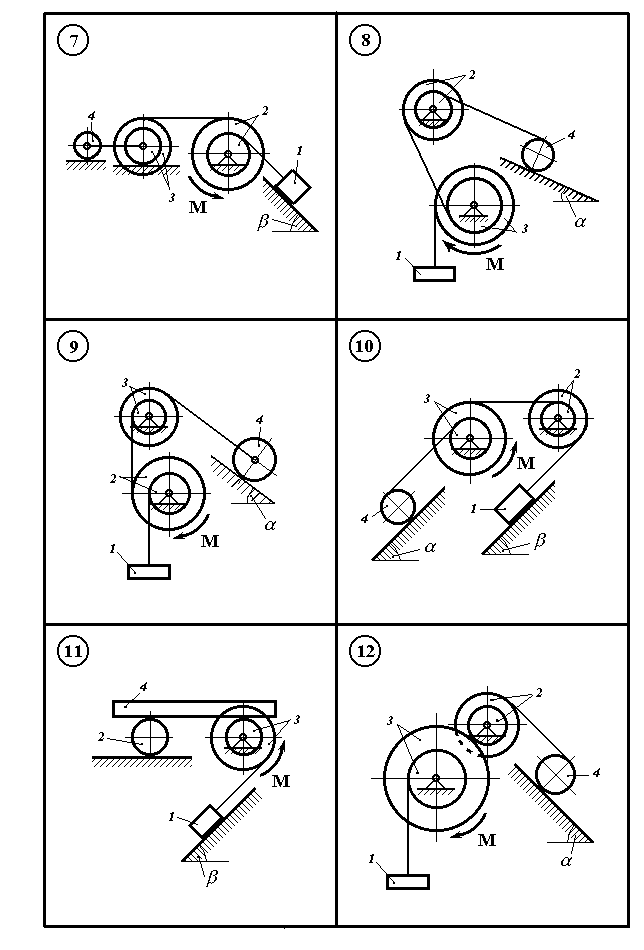 Рисунок 11.2
Рисунок 11.2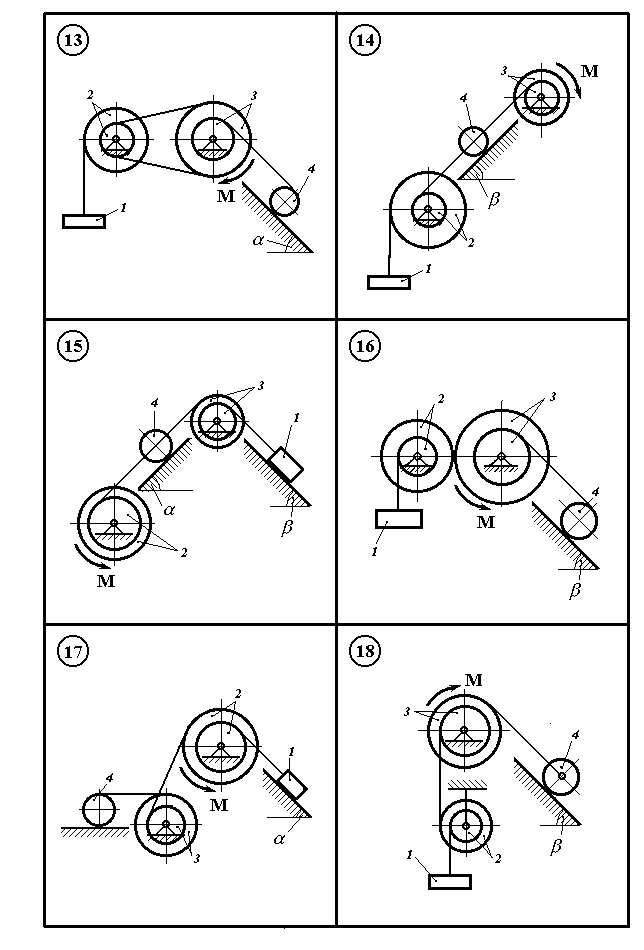

 Рисунок 11.5
Рисунок 11.5
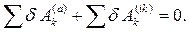 (11.1)
(11.1)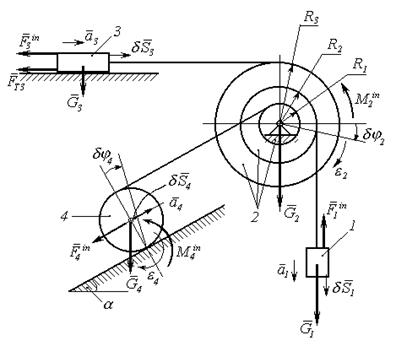
 .
.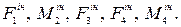
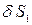 , для тіла 2 –
, для тіла 2 – 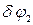 , для тіла 3 –
, для тіла 3 – 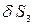 , для тіла 4 –
, для тіла 4 – 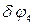 і
і  .
.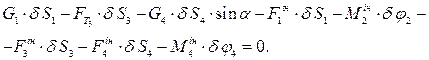 (11.2)
(11.2)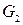 і
і 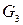 тому, що вони роботи не виконують. Виразимо віртуальні переміщення
тому, що вони роботи не виконують. Виразимо віртуальні переміщення 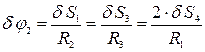 ;
; 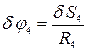 .
. ,
, 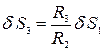 ,
,  ,
, 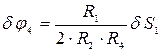 (11.3)
(11.3)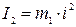 ,
,  . (11.4)
. (11.4)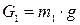 ,
,  ,
, 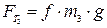 . (11.5)
. (11.5) ,
,  ,
, 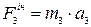 ,
, 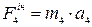 ,
, 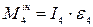 .
. і
і  , а також прискорення
, а також прискорення 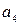 через
через 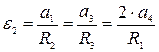 ;
;  ,
,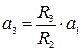 ,
, 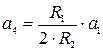 ,
,  .
.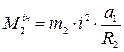 ,
, 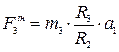 ,
, 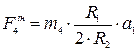 ,
,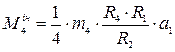 . (11.6)
. (11.6)
 одержуємо рівняння
одержуємо рівняння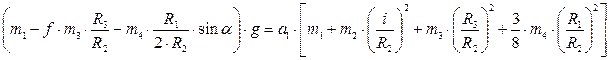
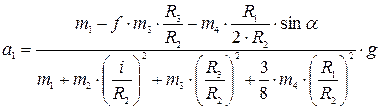 .
. м/с2.
м/с2.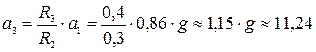 м/с2.
м/с2. Згідно з принципом Даламбера
Згідно з принципом Даламбера .
. .
.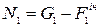 .
.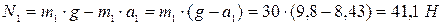 .
. принципу Даламбера
принципу Даламбера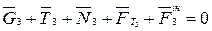 .
.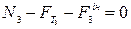 .
. .
.
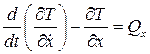 . (12.1)
. (12.1)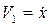 - узагальнена швидкість. Кінетична енергія системи при переміщенні центра мас тіла 1 на величину S1 (підрозділ Д. 5)
- узагальнена швидкість. Кінетична енергія системи при переміщенні центра мас тіла 1 на величину S1 (підрозділ Д. 5) , (12.2)
, (12.2)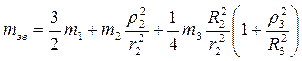 – зведена маса системи.
– зведена маса системи.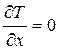 . (12.3)
. (12.3) .
.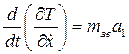 , (12.4)
, (12.4)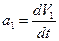 .
. , (12.5)
, (12.5)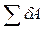 - сума віртуальних робіт активних сил
- сума віртуальних робіт активних сил 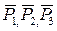 ,
,  і
і 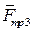 (рис. 12.1);
(рис. 12.1);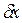 - варіація узагальненої координати х. Горизонтальні складові
- варіація узагальненої координати х. Горизонтальні складові 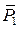 ,
, 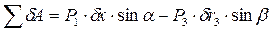 , (12.6)
, (12.6)
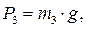
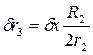 .
.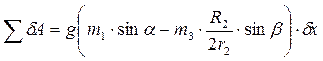 . (12.7)
. (12.7)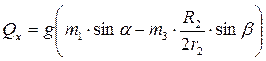 . (12.8)
. (12.8)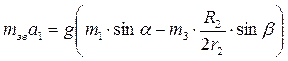
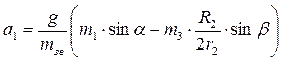 . (12.9)
. (12.9)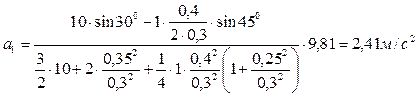 .
. , тоді із формули (12.9) знаходимо швидкість
, тоді із формули (12.9) знаходимо швидкість 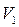
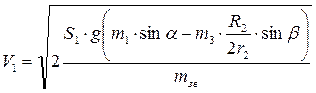 (12.10)
(12.10)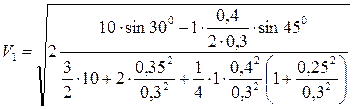 = 1,3 м/с.
= 1,3 м/с.


