Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
А. А. Видмиш, В. О. Приятельчук, В. О. ФедотовСодержание книги
Поиск на нашем сайте А. А. Видмиш, В. О. Приятельчук, В. О. Федотов
Теоретична механіка Динаміка Розрахунково-графічні та контрольні завдання
Вінниця ВНТУ 2009 Міністерство освіти і науки України Вінницький національний технічний університет
А. А. Видмиш, В. О. Приятельчук, В. О. Федотов
Теоретична механіка Динаміка
Розрахунково-графічні та контрольні завдання
Затверджено Вченою радою Вінницького національного університету як навчальний посібник для студентів напряму підготовки 6.050702 – „Електромеханіка”. Протокол № 10 від 27.03. 2008 р.
Вінниця ВНТУ 2009 УДК 531 (075) В 44
Рецензенти: І. О. Сивак, доктор технічних наук, професор В. І. Савуляк, доктор технічних наук, професор О. В. Садовий, доктор технічних наук, професор
Рекомендовано до видання Вченою радою Вінницького національного технічного університету Міністерства освіти і науки України
Видмиш А. А., Приятельчук В. О., Федотов В. О. Теоретична механіка. Динаміка. Розрахунково-графічні та контрольні завдання. Навчальний посібник. – Вінниця: ВНТУ, 2008. -143с. Збірник уміщує 13 завдань із динаміки точки, твердого тіла, матеріальної системи. Кожне завдання має триста варіантів з прикладом виконання. Для студентів денної та заочної форм навчання.
УДК 531(075)
© А. А. Видмиш, В. О. Приятельчук, В. О. Федотов, 2009 Зміст Порядок та основні вимоги до виконання роботи.................................... 5 Розрахунково-графічні та контрольні завдання....................................... 6 ............................................... Динаміка точки……………………………... 6 Д.1 Дослідження руху точки.............................................................. 6 1.1 Приклад виконання завдання........................................................... 10 Динаміка системи…………………………..15 Д.2 Використання теореми про рух центра мас для визначення переміщення тіл........................................................................................ 15 2.1 Приклад виконання завдання........................................................... 21 Д.3 Використання теореми про зміну головного вектора кількості руху системи для дослідження переміщення тіл..................................... 23 3.1 Приклад виконання завдання........................................................... 34 Д.4 Використання теореми про зміну кінетичного моменту для дослідження руху матеріальної системи................................................. 38 4.1 Приклад виконання завдання........................................................... 44 Д.5 Використання теореми про зміну кінетичної енергії для вивчення руху матеріальної системи....................................................... 49 5.1 Приклад виконання завдання............................................................ 55 Д.6 Дослідження руху матеріальної системи із застосуванням основних (загальних) теорем динаміки................................................... 60 6.1 Приклад виконання завдання........................................................... 60 6.1.1 Визначення зусиль в пасах та між тілами..................................... 74 6.1.2 Визначення реакцій циліндричних шарнірів................................ 76 Принцип Д’Аламбера………………….......78 Д.7 Застосування принципу Д’Аламбера для визначення реакції в’язей........................................................................................................ 78 7.1 Приклад виконання завдання........................................................... 84 Д.8 Додаткові динамічні реакції в’язей твердого тіла, що обертається навколо нерухомої осі......................................................... 88 8.1 Приклад виконання завдання........................................................... 88 Принцип Лагранжа……………………….102 Д.9 Визначення реакцій в’язей врівноваженого плоского механізму за допомогою принципу віртуальних переміщень............. 102 9.1 Приклад виконання завдання......................................................... 102 Д.10 Визначення опорних реакцій для складної статичної конструкції за допомогою принципу віртуальних переміщень........... 110 10.1 Приклад виконання завдання....................................................... 110 Загальне рівняння динаміки.......................122 Д.11 Розрахунок характеристик руху механічної системи за допомогою загального рівняння динаміки........................................... 122 11.1 Приклад виконання завдання....................................................... 122
Рівняння Лагранжа 2-го роду…………….132 Д.12 Дослідження руху матеріальної системи з використанням рівняння Лагранжа 2-го роду................................................................ 132 12.1 Приклад виконання завдання....................................................... 132 Д.13 Дослідження вільних коливань матеріальної системи............ 135 13.1 Приклад виконання завдання....................................................... 135 Література........................................................................................... 142
Розрахунково-графічні та контрольні завдання Динаміка точки Д.1 Дослідження руху точки Невільна матеріальна точка масою m (рис.1.1) рухається протягом τ с. по шорсткій поверхні ОА (коефіцієнт тертя ковзання f). В пункті А матеріальна точка із швидкістю Якщо точка рухається під дією постійних сил (табл.1.1), прийняти (рис.1.1), що сила
Рисунок 1.1
Рисунок 1.1 (продовження)
Таблиця 1.1
Таблиця 1.2
Приклад виконання завдання На невільну матеріальну точку масою m, що рухається по похилій шорсткій поверхні ОА (рис. 1.2), діє сила
Рисунок 1.2
Знайти і побудувати траєкторію руху точки на ділянці АВ, її швидкість в пункті В якщо: коефіцієнт тертя ковзання – f = 0,25; початкова швидкість точки v0 = 0,5 м/c; τ = 2 с; d = 2,0 м. Розв’язання. Точка масою m на ділянці ОА переміщується під дією сил: ваги Запишемо закон руху точки на ділянці ОА
в проекціях на осі Х1 та У1.
Рисунок 1.3
Силу тертя знайдемо за законом Амонтона-Кулона, який при переміщені точки з невеликою швидкістю запишеться:
Оскільки точка рухається по прямій ОА, тоді
де Диференціальне рівняння (1.1), враховуючи (1.3) та (1.4) і значення сили F, набуває вигляду:
Або
Інтегруємо диференціальне рівняння (1.5) при початкових умовах: при,
Відстань ОА точка проходить за τ с і її швидкість vA в точці А знаходимо за формулою (1.6) при t1= τ
На ділянці АВ (рис. 1.4) точка рухається під дією сили ваги
Рисунок 1.4
Запишемо диференціальне рівняння руху точки в проекціях на осі Х та У.
де Тоді
Або
При t =0; Оскільки
Інтегруючи рівняння при початкових умовах (1.11), знаходимо:
Або
Інтегруємо рівняння (2.12) та (2.13) при початкових умовах (1.11).
Або
Із рівняння (1.14) та (1.15) знаходимо рівняння траєкторії руху точки на ділянці АВ.
Будуємо траєкторію руху точки (рис.1.5,б), використовуючи рівняння(1.16) (рис. 1.5,а) або формули (1.14) та (1.15).
а) б) Рисунок 1.5
Знайдемо швидкість точки vB. При t2=T, xT=d; тоді із рівняння (1.14) визначаємо час Т руху точки на ділянці АВ.
На підставі рівняння (1.12) та (1.13) визначаємо проекції швидкості
Швидкість точки
На ділянці АВ швидкість точки зменшилась від vA =42,06 м/с до vВ =0,82 м/с,тобто в
Відповідь: Динаміка системи Приклад виконання завдання По похилій площині (рис. 2.6) призми 1 масою m1=10кг спускається вантаж 2 (m2=6кг), який тягне за допомогою невагомої нитки вантаж 3 масою m3=4кг. Знайти переміщення призми 1 по гладенькій горизонтальній площині, якщо тіло m2 опустилось по похилій площині на S=0,5м. Розв’язання. Покажемо зовнішні сили, які прикладені до матеріальної системи, що складається з призми 1 та тіл 2, 3. Такими силами є: P1=m1g – сила ваги призми, P2=m2g i P3=m3g – вага відповідно другого та третього вантажів, N – реакція гладенької горизонтальної поверхні.
Рисунок 2.6
Запишемо теорему про рух центра мас матеріальної системи в проекціях на вісь Х:
де Оскільки В початковий момент часу система знаходилась у спокої і тому
Таким чином, координата ХС центра мас матеріальної системи залишається сталою незалежно від переміщень тіл, що входять у систему. Визначимо положення центра мас системи в початковий момент часу:
Якщо вантаж 2 переміститься на величину
Враховуючи (2.2), із формули (2.3) отримаємо:
Переміщення
Тепер із формули (2.4) знаходимо переміщення призми.
Знак “мінус” вказує на те, що призма 1 перемістилася в сторону, протилежну додатному напрямку осі Х. Відповідь: призма 1 перемістилась вправо на 0,229 м. Приклад виконання завдання Система тіл (рис. 3.11) до якої входить електродвигун 1 масою m2 = 20 кг, однорідний стержень 2 масою m2 = 2 кг та довжиною Система пружин жорсткістю С1=2·103Н/м, С2=3·103Н/м, та С3=4·103Н/м знаходиться у положенні статичної рівноваги. В деякий момент часу точку О зміщують із положення рівноваги вверх на х0=2см і надають швидкість ν0 = 3 м/с вертикально вниз. Одночасно ротор електродвигуна починає обертатись із постійною кутовою швидкістю ω = 1/2·ρ (ρ – частота збурювальної сили) навколо горизонтальної осі. Знайти закон та побудувати графік (при
Рисунок 3.11
Розв’язання. Систему пружин замінюємо однією еквівалентною пружиною жорсткістю С
де С13 = С1·С3 /(С1+С3) = 2·103·4·103/(2·103+4·103) = 4/3·103 Н/м.

Рисунок 3.12
Розглянемо рух невільної системи тіл (рис. 3.11): електродвигуна 1, двох однорідних стержнів 2, двох матеріальних точок А. Центр мас О електродвигуна зміщений із положення статичної рівноваги
Fпр= С· (х+λ), (3.1) де λ – статична деформація пружин, яка знаходиться за формулою λ= (P1+2P2+2PA) /C, де P1,P2,PA – вага відповідно тіл 1,2 та матеріальної точки А. Кутова швидкість обертання ротора
оскільки при явищі резонансу частота збурювальної сили p дорівнює власній частоті коливань системи k= Для дослідження руху корпуса електродвигуна (рис.3.12) використаємо теорему про зміну головного вектора кількості руху системи в проекції на вісь х.
Проекція Qх головного вектора кількості руху системи на вісь х
Використовуючи теорему додавання швидкостей, отримаємо проекцію швидкості точки А і швидкості центра мас тіл 2 на вісь х (рис.3.12).
де Тепер формула (3.4), враховуючи (3.5), запишеться: Qх=
Підставляючи значення Qх (3.6) та Fxe (3.3) в теорему (3.2), отримаємо диференціальне рівняння:
Або
Розв’язок неоднорідного диференціального рівняння (3.7) складається із загального розв’язку однорідного диференціального рівняння
х1=B1coskt + B2 sinkt (3.8)
та частинного розв’язку х2 неоднорідного диференціального рівняння (3.7), який будемо шукати у вигляді:
х2=B3 cosωt. (3.9)
Із (3.7) враховуючи (3.9), знаходимо B3
- ω2B3cosωt + k2B3cosωt = h0cosωt,
Розв’язок неоднорідного диференціального рівняння (3.7)
Постійні інтегрування B1 та B2 визначимо із початкових умов:
Швидкість V точки О (рис.3.12)
Із рівнянь (3.10), (3.12) та початкових умов (3.11) знаходимо постійні інтегрування B1 та B2 . -0,02 = B1+0,007, 3 = 22,86 B2. B2 = 0,13 м; B1 = -0,027м. Тепер рівняння (3.10) руху точки О електродвигуна запишеться: x=-0,027cos(22,86t) +0,13sin(22,86t)+0,007cos(11,43t). (3.13)
Рисунок 3.13
На рис.3.13 наведений графік руху точки О корпуса електродвигуна, який отриманий на підставі формули (3.13).
Відповідь: Приклад виконання завдання
До вантажу 1 (рис. 4.6) масою m1=20кг прив’язаний трос, який перекинутий через нерухомий блок 4 і другий кінець якого закріплений на поверхні шківа 2 радіусом r2 (m2 = 2кг). Механічна система приводиться до руху моментом Знайти закон руху вантажу 1, якщо на тіло 2 діє момент опору МОП = 15 Н×м і при t = 0 кутова швидкість тіла
Рисунок 4.6
Розв’язання. Розглянемо окремо рух тіл 2 і 3 та механізму наведеного на рис. 4.6 До тіла 3 (рис. 4.7) прикладені зовнішні сили: пара сил з моментом М, сила тяжіння P3=m3g, реакції циліндричного шарніра X3 і Y3, реакції тіла 2 – колове зусилля S3 і сила нормального тиску N3. Запишемо диференціальне рівняння обертання тіла 3 навколо нерухомої осі враховуючи, що якщо момент зовнішніх сил діє у напрямку руху тіла, тоді записуємо його з додатним знаком.
де
Таблиця 4.2 - Осьові моменти інерції однорідних тіл
Рисунок 4.7
Початкові умови: при t=0, На тіло 2 (рис. 4.8) діють такі зовнішні сили: сила тяжіння P2=m2g, реакції циліндричного шарніра X2 та Y2, натяг троса S2 (трос працює тільки на розтяг), реакції тіла 3 – Диференціальне рівняння обертання тіла 2 (рис. 4.8) навколо горизонтальної осі Z.
де Оскільки
До тіл 1 та 4 (рис. 4.9) прикладені зовнішні сили: сили тяжіння P1=m1g та P4=m4g, реакція троса
Рисунок 4.8
Теорема про зміну кінетичного моменту для тіл 1 та 4 (рис. 4.9) в проекціях на вісь Z запишеться:
де LZ – кінетичний момент системи тіл 1 та 4 відносно осі Z,
Рисунок 4.9 Кінетичний момент LZ складається із моменту кількості руху LZ1 тіла 1 та кінетичного моменту LZ4 тіла 4 відносно осі Z LZ1 = m1V1R4, (4.6) LZ4 = IZ4ω4. (4.7) Враховуючи, що
Тепер диференціальне рівняння (4.5) набуває вигляду
Якщо до диференціальних рівнянь (4.1), (4.4), (4.8) додати кінематичні співвідношення
тоді отримаємо систему шести рівнянь в які входять невідомі: Розв’язуючи систему рівнянь (4.1), (4.4), (4.8), (4.9) маємо:
З урахуванням того, що m1=20кг, m2=2кг, m3=m4=3кг, r2=0,2м, R2=0,4м, і2=0,3м, R3=R4=0,3м, М = (16+11t2)
Для визначення закону руху тіла 1, інтегруємо двічі диференціальне рівняння (4.10), беручи до уваги початкові умови (4.2)
Перший інтеграл диференціального рівняння (4.10)
Закон руху тіла 1:
Відповідь:
Рисунок 5.1
Рисунок 5.2
Рисунок 5.3
Рисунок 5.4
Рисунок 5.5 Приклад виконання завдання
Визначити прискорення та швидкість центра мас тіла 1 у момент часу, коли він пройде шлях S1, якщо матеріальна система (рис.5.6) починає рухатися із стану спокою. Масами шнурів знехтувати. Тіла 1 та 3 рухаються без ковзання. Дано: m1=10 кг, m2=2 кг, m3=1 кг, R2=0,4 м, r2=0,3м, R3=0,3 м, r3=0,2 м, ρ2=0,35 м, ρ3=0,25 м, α=30˚, β=45˚, S1=0,4 м.
Рисунок 5.6
Розв’язання. Для дослідження
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |




 залишає поверхню ОА і через Тс падає в точку В ділянки АВ із швидкістю
залишає поверхню ОА і через Тс падає в точку В ділянки АВ із швидкістю 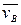 . Знайти і побудувати траєкторію руху точки на ділянці АВ та її швидкість в точці В.
. Знайти і побудувати траєкторію руху точки на ділянці АВ та її швидкість в точці В.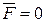 , а при змінних силах (табл. 1.2) сила опору
, а при змінних силах (табл. 1.2) сила опору 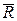 руху точки на ділянці АВ має напрямок протилежний вектору швидкості
руху точки на ділянці АВ має напрямок протилежний вектору швидкості  точки.
точки.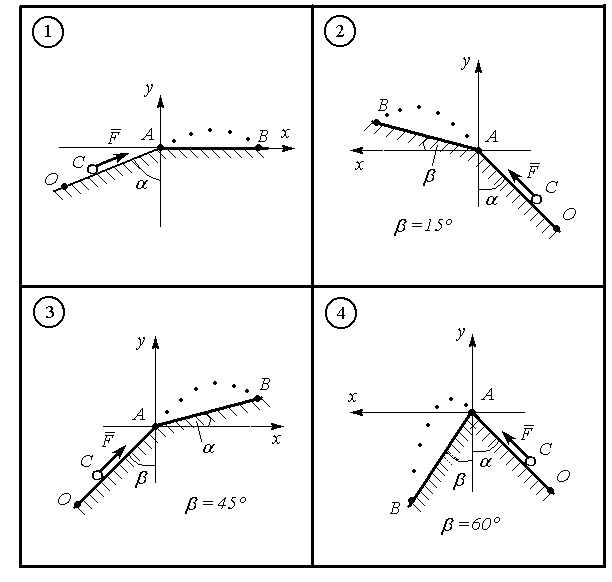

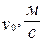
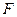 , H
, H

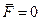
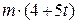


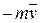

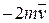
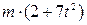

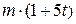
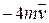

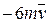

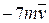
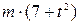
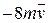



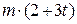



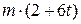
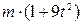

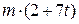



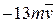
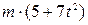

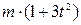
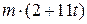
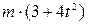
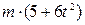
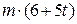

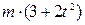
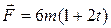 H. Із швидкістю
H. Із швидкістю  Н.
Н.
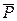 , сили
, сили 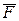 , нормальної реакції
, нормальної реакції 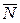 шорсткої поверхні та сили тертя
шорсткої поверхні та сили тертя 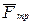 (рис. 1.3).
(рис. 1.3).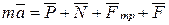
 . (1.1)
. (1.1)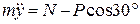 . (1.2)
. (1.2)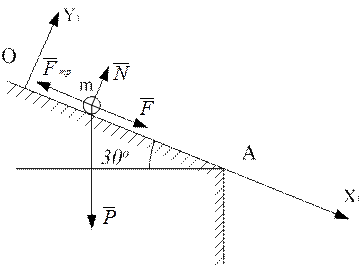
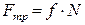 . (1.3)
. (1.3)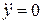 , і з рівняння (1.2) отримаємо:
, і з рівняння (1.2) отримаємо: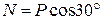 , (1.4)
, (1.4) .
.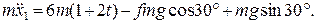
 (1.5)
(1.5)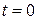 ,
, 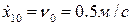 .
.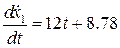 ,
, ,
,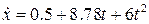 . (1.6)
. (1.6) ,
,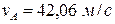 .
.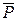 та сили опору
та сили опору  , що направлена в протилежну сторону швидкості точки.
, що направлена в протилежну сторону швидкості точки.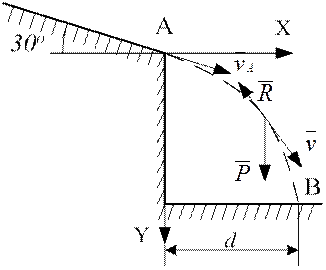
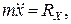 (1.7)
(1.7) . (1.8)
. (1.8)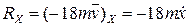 ,
, 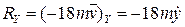 ,
,  .
. .
.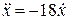 . (1.9)
. (1.9) . (1.10)
. (1.10)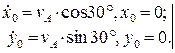 (1.11)
(1.11)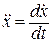 ,
, 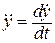 , то в диференціальних рівняннях (1.9) та (1.10), розподіляючи, змінні, отримаємо:
, то в диференціальних рівняннях (1.9) та (1.10), розподіляючи, змінні, отримаємо: ,
,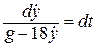 .
.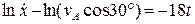 ,
, 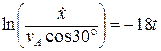 .
.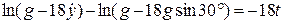 ,
,  .
.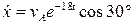 . (1.12)
. (1.12) . (1.13)
. (1.13)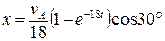 .
.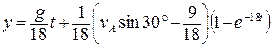 .
. . (1.14)
. (1.14) . (1.15)
. (1.15)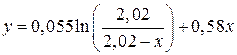 . (1.16)
. (1.16)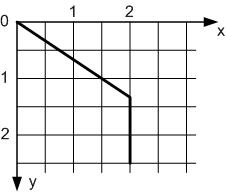
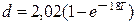 ,
, .
. по осі Х та У (t2=T)
по осі Х та У (t2=T)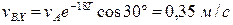 .
.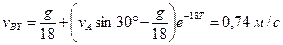 .
. ,
, .
.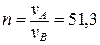 раза за рахунок сили
раза за рахунок сили 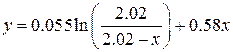 ,
, 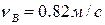 .
.
 , (2.1)
, (2.1) ,
,  - проекція головного вектора зовнішніх сил на вісь Х.
- проекція головного вектора зовнішніх сил на вісь Х. = 0. Тоді
= 0. Тоді  .
. . Із формули (2.1) маємо:
. Із формули (2.1) маємо: .
. . (2.2)
. (2.2) , тоді тіло 3 – на
, тоді тіло 3 – на  , а призма 1 -
, а призма 1 -  і положення ХС центра мас знайдемо за формулою:
і положення ХС центра мас знайдемо за формулою: . (2.3)
. (2.3) . (2.4)
. (2.4) та
та 


 м, матеріальна точка масою mА= 0,5 кг, яка знаходиться в точці А (ОА=2/3
м, матеріальна точка масою mА= 0,5 кг, яка знаходиться в точці А (ОА=2/3  ).
). , де T – період) руху центра мас (точка О) електродвигуна.
, де T – період) руху центра мас (точка О) електродвигуна.

 ,
,
 на величину х (рис. 3.12), а стержні 2 повернулися на кут φ навколо горизонтальної осі О. Дію в’язі (пружину жорсткістю С) замінюємо реакцією в’язі – силою Fпр. Оскільки в точці
на величину х (рис. 3.12), а стержні 2 повернулися на кут φ навколо горизонтальної осі О. Дію в’язі (пружину жорсткістю С) замінюємо реакцією в’язі – силою Fпр. Оскільки в точці  деформація пружин дорівнює нулю, то
деформація пружин дорівнює нулю, то ,
, (m – маса системи)
(m – маса системи) (3.2)
(3.2) ,
,  (3.3)
(3.3) . (3.4)
. (3.4) (3.5)
(3.5) ,
, .
. (
(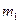 +2m 2 +2m
+2m 2 +2m  )-(
)-(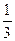 m 2 +
m 2 +  m
m  (3.6)
(3.6) .
. , (3.7)
, (3.7)
 1 +
1 +  х1 =0, а саме:
х1 =0, а саме: .
.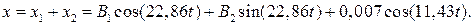 (3.10)
(3.10) .(3.11)
.(3.11)


 , прикладеним до східчастого шківа 3 масою m3=3кг.
, прикладеним до східчастого шківа 3 масою m3=3кг. . Більший радіус у шківа 2 - R2=0,4м, менший – r2 = 0,2м, радіус інерції – і2 = 0,3м. Тіла 3 та 4 мають однакові маси m3=m4 і розміри R3 = R4 = 0,3м. Тіла 2,3 та 4 обертаються навколо горизонтальних нерухомих осей, а тіло 1 переміщується поступально.
. Більший радіус у шківа 2 - R2=0,4м, менший – r2 = 0,2м, радіус інерції – і2 = 0,3м. Тіла 3 та 4 мають однакові маси m3=m4 і розміри R3 = R4 = 0,3м. Тіла 2,3 та 4 обертаються навколо горизонтальних нерухомих осей, а тіло 1 переміщується поступально.
 ,
, - момент інерції тіла відносно осі z;
- момент інерції тіла відносно осі z; - кутове прискорення тіла 3;
- кутове прискорення тіла 3; - момент зовнішніх сил, прикладених до тіла 3, відносно осі z.
- момент зовнішніх сил, прикладених до тіла 3, відносно осі z.

















 . (4.1)
. (4.1) ,
, 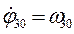 . (4.2)
. (4.2) та
та  , які за третім законом Ньютона направлені в протилежні сторони сил S3 та N3 (рис. 4.7).
, які за третім законом Ньютона направлені в протилежні сторони сил S3 та N3 (рис. 4.7). , (4.3)
, (4.3) - момент інерції тіла 2 відносно осі Z.
- момент інерції тіла 2 відносно осі Z. , то рівняння (4.3) запишеться у вигляді
, то рівняння (4.3) запишеться у вигляді . (4.4)
. (4.4) , реакції циліндричного шарніра X4 та Y4.
, реакції циліндричного шарніра X4 та Y4.
 , (4.5)
, (4.5) - головний момент зовнішніх сил.
- головний момент зовнішніх сил.
 , а
, а  , кінетичний момент системи LZ визначимо за формулою
, кінетичний момент системи LZ визначимо за формулою
 . (4.8)
. (4.8)

 (4.9)
(4.9)
 .
. , M0=15
, M0=15  , отримаємо
, отримаємо . (4.10)
. (4.10)

 м.
м.