
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Д 10 Визначення опорних реакцій для складної статичної конструкції за допомогою принципу віртуальних переміщеньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
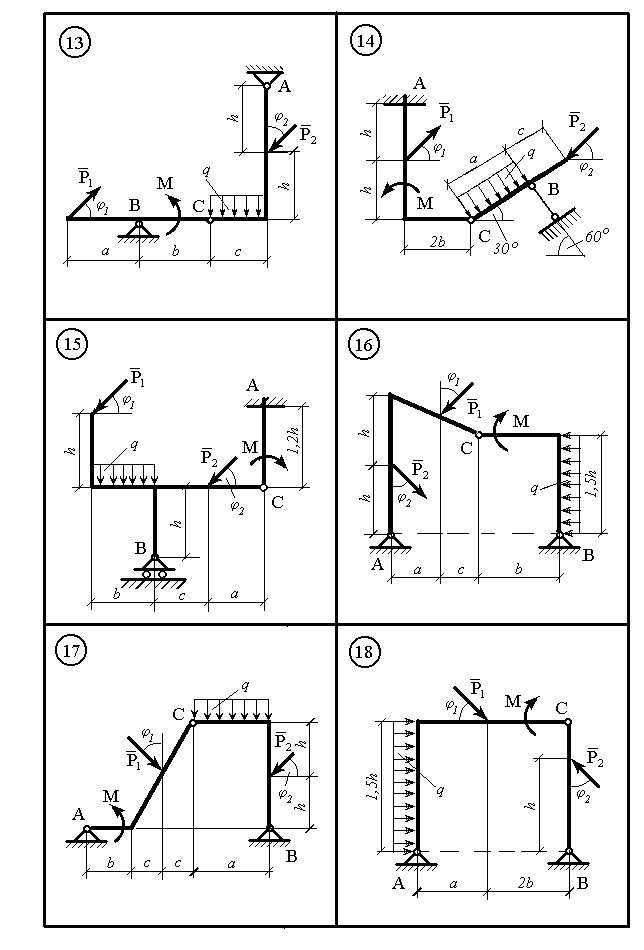
На рис.10.1 – 10.5 по варіантах зображено раму, яка складається з двох частин, з’єднаних між собою шарніром С. Рама закріплена до опор в точках А, В, a в варіантах 1, 5, 6, 7, 23 додатковою опорою в точці D. Рама навантажена силами P1, P2 розподіленим навантаженням інтенсивністю qі моментом М. Напрямки сил P1 і P2 вказуються кутами φ1 і φ2. Визначити опорні реакції рами, використовуючи принцип віртуальних переміщень і виконати статичну перевірку одержаних результатів. В остаточних розрахунках силові навантаження, кути і геометричні розміри взяти в таблиці 10.1 по варіантах.
Таблиця 10.1
Приклад виконання завдання Плоска рама, що зображена на рис.10.6, навантажена силою Визначити опорні реакції заданої рами в точках А і В, виконати статичну перевірку знайдених реакцій. В остаточних розрахунках прийняти:
P= 10 kH; M= 5 kHм; q= 2 kH/м; a= 2 м; b= 3 м; h= 2,5 м. Розв’язання. Опори А і В є плоскими шарнірами, в яких реакції розкладаємо на складові по вертикалі та горизонталі.
Рисунок 10.1
Рисунок 10.2
Рисунок 10.3
Рисунок 10.4
Рисунок 10.5
Рисунок 10.6
Згідно з принципом віртуальних переміщень сума елементарних робіт активних сил рівна нулю:
Щоб знайти силу
Рисунок 10.7 При такій умові рама перетворюється в механізм, де частина рами АС – назвемо її лівою частиною, і ВС – правою частиною, здійснюють віртуальні переміщення як тверді тіла. Ліва частина виконує поворот навколо миттєвого центра точки K1 на кут dj1, а права – навколо центра Вна кут dj2. Складемо рівняння згідно з принципом (10.1) для ситуації зображеної на рис.10.7.
Точка С є спільною для лівої та правої частин, тому:
Звідки
Підставляємо dj1 в формулу (10.2).
Віртуальне переміщення
Попередньо визначимо силу Qрівномірно розподіленого навантаження:
З рис.10.7 визначаємо K1A:
Тоді реакція XA визначається за формулою:
Визначення реакції YA. Надаємо віртуального переміщення dSA в точці Атак, щоб YA стала активною. Тоді створюється така ситуація, яка зображена на рис.10.8. Для правої частини рами центром повороту залишається точка В, а для лівої частини таким центром є точка K2. Віртуальні кутові переміщення для лівої і правої частин рами відповідно рівні dj1 і dj2.
Рисунок 10.8
Складаємо рівняння робіт згідно з принципом (10.1)
По рис.10.8 визначаємо K2A
Реакція YA остаточно буде рівна:
Визначення реакції XB.. Надаємо опорі В віртуального переміщення dSB по горизонталі. Ліва частина набуває віртуального переміщення dj1 навколо центра А, а права – віртуального переміщення dj2 навколо миттєвого центра точки K3, як показано на рис.10.9. Cкладаємо суму віртуальних робіт.
Рисунок 10.9
Знаходимо відстань К3В і співвідношення між переміщеннями dj1 і dj2. по рис.10.9.
Після підстановки К3В та дj2 в рівняння (10.7) і спрощення виразів для XB отримуємо:
Визначаємо реакцію YB. Надаємо точці В вертикальне віртуальне переміщення dS B, отримуємо ситуацію, що зображена на рис.10.10.
Рисунок 10.10
Ліва частина обертається навколо центра А на кут dj1, а права – навколо точки K4 на кут dj2.. Складаємо суму елементарних робіт згідно з (10.1)
Знаходимо K4B і співвідношення між переміщеннями dj1 і dj2..
Тоді:
Підставляємо P, M, Q, α, a, b, h, що задані в умові прикладу. За формулами (10.4), (10.6), (10.8) і (10.10) обчислюємо невідомі реакції.
Виконаємо перевірку знайдених реакцій. Для цього розглянемо розрахункову схему на рис.10.11, де в опорах Аі В зображені складові реакцій і складемо рівняння на основі рівнянь рівноваги для плоскої довільної системи сил в системі координат xAy.
Рисунок 10.11
Якщо реакції знайдені правильно, то повинні виконуватись рівняння:
Складаємо такі рівняння і підставляємо в них дані умови задачі і знайдені реакції.
Таким чином переконуємось, що реакції опор А і В знайдені правильно. Відповідь: ХА=2,296 кН, YA=4,62 кН, ХВ=-7,296 кН, YВ=8,04 кН. Загальне рівняння динаміки
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.45.82 (0.009 с.) |






 , напрямок якої вказує кут
, напрямок якої вказує кут 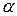 , моментом Мі розподіленням інтенсивності навантаження q. Геометричні розміри рами визначені розмірами a, b, h.
, моментом Мі розподіленням інтенсивності навантаження q. Геометричні розміри рами визначені розмірами a, b, h.




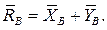

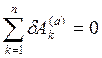 .
.  (10.1)
(10.1) створюємо умови, при яких вона стає активною, тобто виконує роботу. Для цього в опорі А звільняємось від в’язі і надаємо віртуальне переміщення δSA по горизонталі, як показано на рис.10.7.
створюємо умови, при яких вона стає активною, тобто виконує роботу. Для цього в опорі А звільняємось від в’язі і надаємо віртуальне переміщення δSA по горизонталі, як показано на рис.10.7.
 (10.2)
(10.2) (10.3)
(10.3) .
.
 , тому скоротивши на нього, отримуємо:
, тому скоротивши на нього, отримуємо: .
.
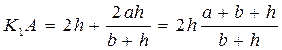 .
. . (10.4)
. (10.4)
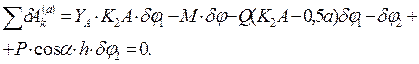
 ;
;

 .
. . (10.6)
. (10.6)


 . (10.7)
. (10.7) ,
,  ,
, ,
,  ,
,  .
. . (10.8)
. (10.8)
 (10.9)
(10.9)



 (10.10)
(10.10) .
. .
. .
. .
.
 ,
,  ,
,  . (10.12)
. (10.12)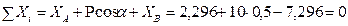 ;
; ;
;




