
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменти інерції деяких однорідних тілСодержание книги Поиск на нашем сайте
3.4.1 Вкажіть правильні вирази моментів інерції тонкого кільця (кругле тіло, маса якого розподілена по його ободу).
3.4.2 Вкажіть правильні вирази моментів інерції однорідної круглої пластини (диска).
3.4.3 Вкажіть правильні вирази моментів інерцій круглого суцільного циліндра.
3.4.4 Вкажіть правильні вирази моментів інерції пустотілого однорідного циліндра (труби).
3.4.5 Вкажіть правильний вираз моменту інерції однорід-ного тонкого стрижня. г)
3.4.6 Вкажіть правильні вирази моментів інерції суцільної кулі.
в)
3.4.7 Вкажіть правильні вирази моментів інерції прямокутної пластини.
а)
4 ЗАГАЛЬНІ ТЕОРЕМИ ДИНАМІКИ 4.1 Теорема про зміну кількості руху
Імпульс сили
4.1.1.1 Імпульс сили – це фізична величина, яка характеризує за деякий проміжок часу. а) – “дію сили на матеріальний об’єкт”;
4.1.1.2 Вкажіть правильну формулу вектора імпульсу змінної сили. б)
4.1.1.3 Вкажіть правильну формулу вектора імпульсу сталої сили. в)
4.1.1.4 Імпульс рівнодійної системи сил за деякий проміжок часу дорівнюєімпульсів складових сил системи за цей же проміжок часу. б) – “геометричній сумі”;
4.1.1.5 Імпульс сили – цевеличина. а) – “векторна”;
4.1.1.6 Вектор елементарного імпульсу сили за напрямом ___________ з вектором сили. в) – “збігається”;
4.1.1.7 Вкажіть правильну одиницю вимірювання імпульсу сили. в) – „Н·с";
4.1.1.8 Вкажіть правильні формули проекції імпульсу змінної сили на декартові осі координат. в)
4.1.1.9 Вкажіть правильні формули проекції імпульсу змінної сили на декартові осі координат. д)
4.1.1.10 Вкажіть правильні вирази напрямних конусів вектора імпульсу сили а)
4.1.1.11 Вкажіть правильний вираз імпульсу сили, якщо його проекції на декортові осі координат в)
4.1.2 Кількість руху матеріальної точки і
4.1.2.1 Кількістю руху матеріальної точки називають а) – “добутку маси точки на її швидкість”;
4.1.2.2 Кількість руху матеріальної точки ____________величина. б) – “векторна”;
4.1.2.3 Вкажіть правильну одиницю вимірювання кількості руху. г) – „кг·м/с”;
4.1.2.4 Вкажіть правильну формулу кількості руху матеріальної точки. б) 4.1.2.5 Кількість руху матеріальної точки є вектор, який за напрямкомшвидкості точки. б) – “збігається з вектором”;
4.1.2.6 Вкажіть правильний рисунок напрямку вектора
4.1.2.7 Вкажіть правильні вирази проекції вектора кількості руху на декартові осі координат. а)
4.1.2.8 Вкажіть правильні вирази проекції вектора кількості руху на декартові осі координат. в)
4.1.2.9 Кількістю руху механічної системи називають _______________ кількостей руху всіх матеріальних точок даної системи. б) – “векторну суму (головний вектор)”; 4.1.2.10 Вкажіть правильний вираз кількості руху механічної системи (головного вектора кількості руху). в) 4.1.2.11 Вкажіть правильний вираз кількості руху механічної системи (головного вектора кількості руху). в)
4.1.2.12 Кількість руху механічної системи дорівнює ________ її центра мас. б) – “добутку маси системи на швидкість”;
4.1.2.13 Вкажіть правильні вирази проекції вектора кількості руху механічної системи на декартові осі координат. в)
4.1.2.14 Вкажіть правильні вирази проекції вектора кількості руху механічної системи на декартові осі координат. а)
4.1.2.15 Кількість руху є міроюруху. г) – “механічного”;
4.1.3 Теорема про зміну кількості руху
4.1.3.1 Перша похідна за часом від кількості руху матері-альної точки дорівнюєсумі всіх сил, що діють на точку. в) – “геометричній”;
4.1.3.2 Перша похідна за часом від кількості руху матеріальної точки дорівнює геометричній сумі ________ сил, що діють на точку. а) – “всіх”;
4.1.3.3 Вкажіть правильний вираз теореми про зміну кількості руху матеріальної точки в диференціальній формі. д) 4.1.3.4 Диференціал від кількості руху матеріальної точки дорівнюєсумі елементарних імпульсів всіх сил, що діють на точку. а) – “геометричній”;
4.1.3.5 Диференціал від кількості руху матеріальної точки дорівнює геометричній сумі елементарних імпульсів ________ сил, що діють на точку. б) – “всіх”;
4.1.3.6 Вкажіть правильний вираз теореми про зміну кількості руху матеріальної точки в диференціальній формі. г) 4.1.3.7 Зміна кількості руху матеріальної точки за деякий проміжок часу дорівнюєсумі імпульсів всіх сил, що діють на точку, за цей же проміжок часу. в) – “геометричній”;
4.1.3.8 Зміна кількості руху матеріальної точки за деякий проміжок часу дорівнює геометричній сумі імпульсів ________ сил, що діють на точку, за цей же проміжок часу. б) – “всіх”;
4.1.3.9 Вкажіть правильний вираз теореми про зміну кількості руху матеріальної точки в інтегральній (кінцевій) формі за деякий проміжок часу. д)
4.1.3.10 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. а)
4.1.3.11 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. в) 4.1.3.12 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. г) 4.1.3.13 Вкажіть правильні інтегральні (в кінцевій формі) вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. д) 4.1.3.14 Вкажіть правильні інтегральні (в кінцевій формі) вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. б) 4.1.3.15 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. б)
4.1.3.16 Перша похідна за часом від кількості руху механічної системи дорівнюєсумі (головному вектору) всіх зовнішніх сил, що діють на систему. б) – “геометричній”;
4.1.3.17 Перша похідна за часом від кількості руху механічної системи дорівнює геометричній сумі (головному вектору) всіх ________ сил, що діють на систему. в) – “зовнішніх”;
4.1.3.18 Вкажіть правильний вираз теореми про зміну б)
4.1.3.19 Вкажіть правильний вираз теореми про зміну кількості руху механічної системи в диференціальній формі. в)
4.1.3.20 Диференціал від кількості руху механічної системи дорівнюєсумі елементарних імпульсів всіх зовнішніх сил, що діють на систему. б) – “геометричній”;
4.1.3.21 Диференціал від кількості руху механічної системи дорівнює геометричній сумі елементарних __________ сил, що діють на систему. в) – “імпульсів всіх зовнішніх”;
4.1.3.22 Зміна кількості руху механічної системи за деякий проміжок часу дорівнюєсумі імпульсів всіх зовнішніх сил, що діють на систему, за цей же проміжок часу. а) – “геометричній”;
4.1.3.23 Зміна кількості руху механічної системи за деякий проміжок часу дорівнює геометричній сумі _________ сил, що діють на систему, за цей же проміжок часу. в) – “імпульсів всіх зовнішніх”;
4.1.3.24 Вкажіть правильний вираз теореми про зміну кількості руху механічної системи в інтегральній формі. в)
4.1.3.25 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху механічної системи в проекціях на декартові осі координат.
4.1.3.26 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху механічної системи в проекціях на декартові осі координат. а) 4.1.3.27 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху механічної системи в проекціях на декартові осі координат. а) 4.1.3.28 Вкажіть правильні інтегральні (в кінцевій формі) вирази теореми про зміну кількості руху механічної системи в проекціях на декартові осі координат. б) 4.1.3.29 Зміна кількості руху механічної системи зумовленасилами, що діють на систему. б) – “тільки зовнішніми”;
4.1.3.30 Якщо головний вектор зовнішніх сил, що діють на систему, дорівнює нулеві б) – “не зміниться”;
4.1.3.31 Якщо головний вектор зовнішніх сил, що діють на систему _____________, то кількість руху механічної системи не зміниться. а) – “дорівнює нулеві”;
4.1.3.32 Вкажіть правильні вирази закону збереження б) Якщо
4.1.3.33 Якщо проекція головного вектора зовнішніх сил, що діють на систему, на деяку вісь, то проекція кількості руху системи на дану вісь не зміниться. б) – “дорівнює нулеві”;
4.1.3.34 Якщо проекція головного вектора зовнішніх сил, що діють на систему, на деяку вісь дорівнює нулеві, то проекція кількості руху системи на дану вісь ___________. в) – “не зміниться”;
4.1.3.35 Вкажіть правильні вирази закону збереження кількості руху механічної системи по осі абсцис. а) Якщо Теорема Ейлера 4.1.4.1 Сума векторів секундних кількостей руху рідини, що протікає через два поперечні перерізи труби, які нап-равлені у середину виділеного об’єму, а також головних векторівсил, дорівнює нулеві. в) – “об’ємних і поверхневих”;
4.1.4.2 Вкажіть правильний запис формули Ейлера для дослідження руху суцільного середовища. д)
4.1.4.3 Вкажіть правильні записи формули Ейлера для дослідження руху суцільного середовища в проекціях на декартові осі координат.
4.1.4.4 Вкажіть правильні записи формули Ейлера для дослідження руху суцільного середовища в проекціях на декартові осі координат.
4.2 Теорема про рух центра мас механічної системи
4.2.1 Центр мас механічної системи рухається як матеріальна точка, в якій зосереджена вся маса системи і до якої прикладені всі __ сили, що діють на систему. б) – “зовнішні”;
4.2.2 Центр мас механічної системи ____________, в якій зосереджена вся маса системи і до якої прикладені всі зовнішні сили, що діють на систему. б) – “рухається як матеріальна точка”; 4.2.3 Вкажіть правильну формулу теореми про рух центра мас механічної системи. д)
4.2.4 Вкажіть правильну формулу теореми про рух центра мас механічної системи. д)
4.2.5 Вкажіть правильну формулу теореми про рух центра мас механічної системи. б) 4.2.6 Вкажіть правильну формулу теореми про рух центра мас механічної системи (маса системи не змінюється з часом). а) 4.2.7 Вкажіть правильні формули теореми про рух центра мас механічної системи в проекціях на декартові осі координат. в)
4.2.8 Вкажіть правильні формули теореми про рух центра мас механічної системи в проекціях на декартові осі координат. б) 4.2.9 На рух центра мас механічної системи впливають тільки _____________ сили, що діють на систему. б) – “зовнішні”; 4.2.10 Якщо головний вектор б) – “дорівнює нулеві”; 4.2.11 Якщо головний вектор б) – “незалежно від початкових умов”; 4.2.12 Якщо головний вектор б) – “рівномірно і прямолінійно”; 4.2.13 Вкажіть правильний вираз збереження руху центра мас системи. а) Якщо 1) якщо 2) якщо 4.2.14 Якщо проекція головного вектора зовнішніх сил, що діють на систему, на деяку вісьто проекція швидкості центра мас на цю вісь не змінюється, тобто є інтегралом руху. а) – “дорівнює нулеві”;
4.2.15 Вкажіть правильний вираз в проекції на вісь Ох закону збереження руху центра мас системи. в) Якщо 1) якщо 2) якщо 4.2.16 Вкажіть правильний вираз в проекції на вісь Оу закону збереження руху центра мас системи. б) Якщо 1) якщо 2) якщо
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


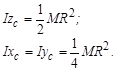
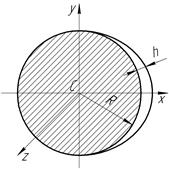


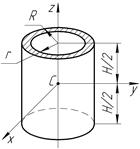

 ;
;

 ;
;

 3.4.8 Вкажіть правильний вираз моменту інерції механічної системи відносно осі, що проходить через початок системи координат і утворює з координатними осями Ох, Оу, Oz відповідно кути α, β, γ.
3.4.8 Вкажіть правильний вираз моменту інерції механічної системи відносно осі, що проходить через початок системи координат і утворює з координатними осями Ох, Оу, Oz відповідно кути α, β, γ.
 ;
;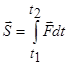 ;
; ;
; .
. .
. .
. ;
; i
i  .
. ;
;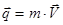 ;
;
 ;
; ;
; ;
; ;
; ;
; ;
;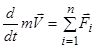 .
. ;
; .
. ;
; ;
;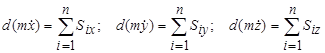 ;
; .
. ;
; ;
; ;
; ;
; ;
;
 ;
; ;
;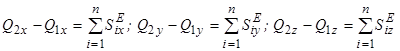 ;
; , то кількість руху механічної системи _____________.
, то кількість руху механічної системи _____________. , то
, то  ;
; , то
, то  ;
; .
.

 .
. .
. ;
; ;
; ;
; ;
; зовнішніх сил, що діють на систему,, то центр мас її залежно від початкових умов рухається рівномірно і прямолінійно або не змінює свого положення.
зовнішніх сил, що діють на систему,, то центр мас її залежно від початкових умов рухається рівномірно і прямолінійно або не змінює свого положення. зовнішніх сил, що діють на систему, дорівнює нулеві, то центр мас їїрухається рівномірно і прямолінійно або не змінює свого положення.
зовнішніх сил, що діють на систему, дорівнює нулеві, то центр мас їїрухається рівномірно і прямолінійно або не змінює свого положення. , то
, то  ; при цьому:
; при цьому: , то
, то  , тобто, центр мас руха-
, тобто, центр мас руха- , то
, то  , тобто, центр мас системи не змінює свого положення.
, тобто, центр мас системи не змінює свого положення. , то
, то  ; при цьому:
; при цьому: , то
, то  , тобто, центр мас по осі Ох рухається рівномірно;
, тобто, центр мас по осі Ох рухається рівномірно; , то
, то  , тобто, центр мас системи по осі Ох не змінює свого положення.
, тобто, центр мас системи по осі Ох не змінює свого положення. , то
, то  ; при цьому:
; при цьому: , то
, то  , тобто, центр мас по осі Оу рухається рівномірно.
, тобто, центр мас по осі Оу рухається рівномірно. , то
, то  , тобто, центр мас системи по осі Оу не змінює свого положення.
, тобто, центр мас системи по осі Оу не змінює свого положення.


