
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальні рівняння руху матеріальної точкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Вхідні поняття динаміки 1.1.1 Динамікою називають розділ теоретичної механіки, в якому вивчають механічний рух матеріальної точки, системи матеріальних точок і абсолютно твердого тіла з урахуванням ____________, що діють на ці рухомі об’єкти. а) – “сил”;
1.1.2 Динамікою називають розділ теоретичної механіки в якому вивчають ______________ матеріальної точки, системи матеріальних точок і абсолютно твердого тіла з урахуванням сил, що діють на ці рухомі об’єкти. в) – “механічний рух”;
1.1.3 Динамікою називають розділ теоретичної механіки в якому вивчають механічний рух матеріальної точки, системи матеріальних точок і абсолютно твердого тіла з урахуванням сил, __________ на ці рухомі об’єкти. б) – “що діють”;
1.1.4 Виберіть правильне закінчення твердження. Динамікою називають розділ теоретичної механіки, в якому вивчають механічний рух ______________. г) – “матеріальної точки, системи матеріальних точок і абсолютно твердого тіла з урахуванням сил, що діють на ці об’єкти”;
1.1.5 Сила повністю характеризується: в) – “точкою прикладення, числовим значенням і напрямом”;
1.1.6 Вкажіть правильне закінчення означення: інерціальними системами координат називають ___________. в) – “системи координат, у яких справедливі закони Ньютона”;
1.1.7 Виберіть правильне закінчення означення: матері-альна точка – це ____________. в) – “матеріальний об’єкт, розмірами якого в умовах даної задачі можна знехтувати”;
1.1.8 Маса точки – це фізична величина, яка є мірою її ___. в) – “інерційних і гравітаційних властивостей”; Основні закони динаміки 1.2.1 Дайте правильне формулювання І-го закону Ньютона (закону інерції). Матеріальна точка зберігає стан спокою або рівномірного прямолінійного руху доти, поки, _____________. б) – “дія інших тіл не змінить цього стану”;
1.2.2 Дайте правильне формулювання І-го закону Ньютона (закону інерції). Матеріальна точка _____________ доти, поки дія інших тіл не змінить цього стану. в) – “зберігає стан спокою або рівномірного прямолінійного руху”;
1.2.3 Дайте правильне закінчення формулювання ІІ-го закону Ньютона (основного закону механіки; закону сили). Добуток маси точки на її вектор пришвидшення дорівнює _____________. в) – “вектору сили, прикладеної до точки, а напрям пришвидшення збігається з напрямом цього вектора”;
1.2.4 Дайте правильне закінчення формулювання ІІ-го закону Ньютона (основного закону механіки; закону сили). Добуток маси точки на її вектор пришвидшення дорівнює _______________. а) – “вектору сили, прикладеної до точки, а напрям пришвидшення збігається з напрямом цього вектора”;
1.2.5 Дайте правильне формулювання ІІ-го закону Ньютона (основного закону механіки; закону сили). Швидкість зміни кількості руху матеріальної точки дорівнює силі, що діє на точку, і спрямована ___________. б) – “в напрямі дії сили”;
1.2.6 Вкажіть правильний вираз рівності, яка виражає ІІ-й закон Ньютона (основний закон механіки; закон сили). в)
1.2.7 Дайте правильне формулювання ІІ-го закону Ньютона (основного закону механіки; закону сили). Швидкість зміни кількості руху матеріальної точки дорівнює силі, що діє на точку і спрямована __________. б) – “в напрямі дії сили”;
1.2.8 Дайте правильне закінчення формулювання закону незалежності дії сили. Якщо на матеріальну точку діє система сил, то пришвидшення, з яким рухається матеріальна точка, дорівнює ____________ пришвидшень, що викликаються кожною силою окремо. в) – “геометричній сумі”;
1.2.9 Вкажіть правильний вираз рівності, яка виражає закон незалежності дії сил: г)
1.2.10 Дайте правильне формулювання ІІІ-го закону Ньютона (закону дії і протидії). Кожна механічна дія супроводжується _______протидією. в) – “рівною і протилежно спрямованою”;
1.2.11 Вкажіть правильний вираз, який виражає ІІІ-й закон Ньютона (закон дії і протидії). а)
1.2.12 Вкажіть, що виражає ІІІ-й закон Ньютона: в) – “рівність дії і протидії між двома матеріальними тілами”;
1.2.13 Вкажіть правильне формулювання ІІІ-го закону Ньютона (закону дії і протидії). Дві матеріальні точки діють одна на одну із ___________. б) – “силами однаковими за модулем і протилежними за напрямом”;
1.2.14 Вкажіть правильне формулювання ІІІ-го закону Ньютона (закону дії і протидії). Дві матеріальні точки діють одна на одну із ___________. в) – “силами однаковими за модулем і протилежними за напрямом”;
1.2.15 Вкажіть правильний вираз, який виражає основне рівняння динаміки матеріальної точки. в)
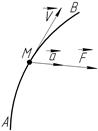
1.2.16 Вкажіть правильний рисунок, який графічно пояснює основне рівняння динаміки.
1.2.17 Вкажіть правильний вираз, який виражає ІІ-й закон Ньютона (основний закон механіки; закон сили). в) 1.2.18 Вкажіть правильний вираз, який виражає ІІ-й закон Ньютона (основний закон механіки; закон сили). в) 1.2.19 Вкажіть правильний вираз, який виражає основне рівняння динаміки. в) 1.2.20 Вкажіть правильний вираз, за яким можна визначити величину ваги тіла Р. в) Перша задача динаміки
2.2.1 Дайте правильне формулювання визначення першої задачі динаміки. Пряма, або перша основна, задача динаміки матеріальної точки полягає у визначенні, за заданими її масою m і кінематичними характеристиками (рівняння руху, швидкість, пришвидшення) її руху. а) – “рівнодійної 2.2.2 Дайте правильне формулювання визначення першої задачі динаміки. Пряма, або перша основна, задача динаміки матеріальної точки полягає у визначенні рівнодійної в) – “масою m і кінематичними характеристиками (рівняння руху, швидкість, пришвидшення) її руху”; 2.2.3 Вкажіть правильні вирази, за якими знаходять модуль рівнодійної ; в)
2.2.4 Вкажіть правильні вирази розв’язку прямої задачі динаміки матеріальної точки під дією сили д)
2.2.5 Вкажіть правильні вирази розв’язку прямої задачі динаміки матеріальної точки під дією сили б)
2.2.6 Вкажіть правильне формулювання першої задачі динаміки матеріальної точки. б) – “за відомими масою точки та рівняннями її руху знайти модуль і напрям рівнодійної сил, прикладених до точки”;
2.2.7 Вкажіть правильне продовження твердження: З допомогою диференціальних рівнянь руху матеріальної точки в тій чи іншій системі координат. в) – “розв’язується дві основні задачі (пряма та обернена) динаміки точки”; 2.2.8 Вкажіть правильне формулювання першої задачі динаміки матеріальної точки. в) – “за відомими масою точки і законом її руху, знайти модуль і напрям рівнодійної сил, що діють на точку”;
Друга задача динаміки
2.3.1 Вкажіть правильне закінчення формулювання другої задачі динаміки. Обернена або друга основна, задача динаміки матеріальної точки полягає у визначенні в) – “кінематичних характеристик руху за заданими масою m точки, силами, що діють на неї і початковими кінематичними характеристиками”;
2.3.2 Вкажіть диференціальне рівняння прямолінійного руху матеріальної точки і відповідні початкові кінематичні характеристики. а) г) 2.3.3 Кінцевою метою розв’язування оберненої задачі динаміки матеріальної точки найчастіше є визначення____. б) – “кінематичних рівнянь руху точки”; 2.3.4 Вкажіть правильне диференціальне рівняння прямолінійного руху точки і відповідні повні початкові умови її руху. д) 2.3.5 Вкажіть правильне диференціальне рівняння прямолінійного руху точки і відповідні повні початкові умови її руху. г) 2.3.6 Вкажіть правильне диференціальне рівняння прямолінійного руху точки і відповідні повні початкові умови її руху. д) 2.3.7 Вкажіть правильні диференціальні рівняння руху точки в площині Оху і відповідні повні початкові умови її руху.
2.3.8 Вкажіть правильне закінчення твердження: Сталі інтегрування диференціальних рівнянь руху матеріальної точки визначають в) – “положення і швидкості точки у початковий момент часу”;
2.3.9 Вкажіть правильні математичні записи змісту другої задачі динаміки точки. г) Відомі:
2.3.10 Вкажіть правильні диференціальні рівняння руху точки в площині Оyz і відповідні повні початкові умови її руху.
2.3.11 Вкажіть правильні диференціальні рівняння руху точки в площині Оxz і відповідні повні початкові умови її руху.
2.3.12 Вкажіть правильні повні вирази початкових умов руху точки в декартовій системі координат в початковий момент часу. б) 2.3.13 Дайте правильне закінчення твердження. Початкові умови, які задаються при розв’язуванні другої (оберненої) задачі динаміки точки, визначають _________. а) – “єдиний розв’язок системи диференціальних рівнянь руху точки”. 2.3.14 Вкажіть повне закінчення твердження: Для визначення сталих інтегрування при розв’язуванні другої задачі динаміки точки для початкового моменту часу задають б) – “координати руху точки 2.3.15 Вкажіть правильні вирази повних початкових умов руху точки в площині Оху. а) 2.3.16 Вкажіть правильні вирази повних початкових умов руху точки в площині Оуz. г) 2.3.17 Вкажіть правильні вирази повних початкових умов руху точки в площині Охz. в)
2.3.18 Вкажіть правильні вирази повних початкових умов руху точки вздовж осі Ох. б) 2.3.19 Вкажіть правильні вирази повних початкових умов руху точки вздовж осі Оу. в) 2.3.20 Вкажіть правильні вирази повних початкових умов руху точки вздовж осі Оz. г) 2.4 Диференціальні рівняння руху
2.4.1 Вкажіть правильне закінчення означення невільного руху матеріальної точки. Рух матеріальної точки є невільним, якщо вона із-за накладених в’язей вимушена рухатись а) – “по заданій поверхні або кривій”;
2.4.2 Вкажіть правильні вирази диференціальних рівнянь руху невільної матеріальної точки по гладкій поверхні б) 2.4.3 Вкажіть правильні вирази множників Лагранжа в диференціальних рівняннях руху невільної матеріальної точки по гладкій кривій, яка утворена перетином двох поверхонь б)
2.4.4 Вкажіть правильний вираз множника Лагранжа в диференціальних рівняннях руху невільної матеріальної точки по гладкій поверхні, рівняння якої а) 2.4.5 Вкажіть правильні вирази диференціальних рівнянь Лагранжа першого роду руху точки по гладкій лінії, яка утворена перетином двох поверхонь
Динамічні рівняння Ейлера
2.9.1 Вкажіть правильні вирази диференціальних рівнянь обертання твердого тіла навколо нерухомої точки, які називають динамічними рівняннями Ейлера.
Імпульс сили
4.1.1.1 Імпульс сили – це фізична величина, яка характеризує за деякий проміжок часу. а) – “дію сили на матеріальний об’єкт”;
4.1.1.2 Вкажіть правильну формулу вектора імпульсу змінної сили. б)
4.1.1.3 Вкажіть правильну формулу вектора імпульсу сталої сили. в)
4.1.1.4 Імпульс рівнодійної системи сил за деякий проміжок часу дорівнюєімпульсів складових сил системи за цей же проміжок часу. б) – “геометричній сумі”;
4.1.1.5 Імпульс сили – цевеличина. а) – “векторна”;
4.1.1.6 Вектор елементарного імпульсу сили за напрямом ___________ з вектором сили. в) – “збігається”;
4.1.1.7 Вкажіть правильну одиницю вимірювання імпульсу сили. в) – „Н·с";
4.1.1.8 Вкажіть правильні формули проекції імпульсу змінної сили на декартові осі координат. в)
4.1.1.9 Вкажіть правильні формули проекції імпульсу змінної сили на декартові осі координат. д)
4.1.1.10 Вкажіть правильні вирази напрямних конусів вектора імпульсу сили а)
4.1.1.11 Вкажіть правильний вираз імпульсу сили, якщо його проекції на декортові осі координат в)
4.1.2 Кількість руху матеріальної точки і
4.1.2.1 Кількістю руху матеріальної точки називають а) – “добутку маси точки на її швидкість”;
4.1.2.2 Кількість руху матеріальної точки ____________величина. б) – “векторна”;
4.1.2.3 Вкажіть правильну одиницю вимірювання кількості руху. г) – „кг·м/с”;
4.1.2.4 Вкажіть правильну формулу кількості руху матеріальної точки. б) 4.1.2.5 Кількість руху матеріальної точки є вектор, який за напрямкомшвидкості точки. б) – “збігається з вектором”;
4.1.2.6 Вкажіть правильний рисунок напрямку вектора
4.1.2.7 Вкажіть правильні вирази проекції вектора кількості руху на декартові осі координат. а)
4.1.2.8 Вкажіть правильні вирази проекції вектора кількості руху на декартові осі координат. в)
4.1.2.9 Кількістю руху механічної системи називають _______________ кількостей руху всіх матеріальних точок даної системи. б) – “векторну суму (головний вектор)”; 4.1.2.10 Вкажіть правильний вираз кількості руху механічної системи (головного вектора кількості руху). в) 4.1.2.11 Вкажіть правильний вираз кількості руху механічної системи (головного вектора кількості руху). в)
4.1.2.12 Кількість руху механічної системи дорівнює ________ її центра мас. б) – “добутку маси системи на швидкість”;
4.1.2.13 Вкажіть правильні вирази проекції вектора кількості руху механічної системи на декартові осі координат. в)
4.1.2.14 Вкажіть правильні вирази проекції вектора кількості руху механічної системи на декартові осі координат. а)
4.1.2.15 Кількість руху є міроюруху. г) – “механічного”;
4.1.3 Теорема про зміну кількості руху
4.1.3.1 Перша похідна за часом від кількості руху матері-альної точки дорівнюєсумі всіх сил, що діють на точку. в) – “геометричній”;
4.1.3.2 Перша похідна за часом від кількості руху матеріальної точки дорівнює геометричній сумі ________ сил, що діють на точку. а) – “всіх”;
4.1.3.3 Вкажіть правильний вираз теореми про зміну кількості руху матеріальної точки в диференціальній формі. д) 4.1.3.4 Диференціал від кількості руху матеріальної точки дорівнюєсумі елементарних імпульсів всіх сил, що діють на точку. а) – “геометричній”;
4.1.3.5 Диференціал від кількості руху матеріальної точки дорівнює геометричній сумі елементарних імпульсів ________ сил, що діють на точку. б) – “всіх”;
4.1.3.6 Вкажіть правильний вираз теореми про зміну кількості руху матеріальної точки в диференціальній формі. г) 4.1.3.7 Зміна кількості руху матеріальної точки за деякий проміжок часу дорівнюєсумі імпульсів всіх сил, що діють на точку, за цей же проміжок часу. в) – “геометричній”;
4.1.3.8 Зміна кількості руху матеріальної точки за деякий проміжок часу дорівнює геометричній сумі імпульсів ________ сил, що діють на точку, за цей же проміжок часу. б) – “всіх”;
4.1.3.9 Вкажіть правильний вираз теореми про зміну кількості руху матеріальної точки в інтегральній (кінцевій) формі за деякий проміжок часу. д)
4.1.3.10 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. а)
4.1.3.11 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. в) 4.1.3.12 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. г) 4.1.3.13 Вкажіть правильні інтегральні (в кінцевій формі) вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. д) 4.1.3.14 Вкажіть правильні інтегральні (в кінцевій формі) вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. б) 4.1.3.15 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху матеріальної точки в проекціях на декартові осі координат. б)
4.1.3.16 Перша похідна за часом від кількості руху механічної системи дорівнюєсумі (головному вектору) всіх зовнішніх сил, що діють на систему. б) – “геометричній”;
4.1.3.17 Перша похідна за часом від кількості руху механічної системи дорівнює геометричній сумі (головному вектору) всіх ________ сил, що діють на систему. в) – “зовнішніх”;
4.1.3.18 Вкажіть правильний вираз теореми про зміну б)
4.1.3.19 Вкажіть правильний вираз теореми про зміну кількості руху механічної системи в диференціальній формі. в)
4.1.3.20 Диференціал від кількості руху механічної системи дорівнюєсумі елементарних імпульсів всіх зовнішніх сил, що діють на систему. б) – “геометричній”;
4.1.3.21 Диференціал від кількості руху механічної системи дорівнює геометричній сумі елементарних __________ сил, що діють на систему. в) – “імпульсів всіх зовнішніх”;
4.1.3.22 Зміна кількості руху механічної системи за деякий проміжок часу дорівнюєсумі імпульсів всіх зовнішніх сил, що діють на систему, за цей же проміжок часу. а) – “геометричній”;
4.1.3.23 Зміна кількості руху механічної системи за деякий проміжок часу дорівнює геометричній сумі _________ сил, що діють на систему, за цей же проміжок часу. в) – “імпульсів всіх зовнішніх”;
4.1.3.24 Вкажіть правильний вираз теореми про зміну кількості руху механічної системи в інтегральній формі. в)
4.1.3.25 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху механічної системи в проекціях на декартові осі координат.
4.1.3.26 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху механічної системи в проекціях на декартові осі координат. а) 4.1.3.27 Вкажіть правильні диференціальні вирази теореми про зміну кількості руху механічної системи в проекціях на декартові осі координат. а) 4.1.3.28 Вкажіть правильні інтегральні (в кінцевій формі) вирази теореми про зміну кількості руху механічної системи в проекціях на декартові осі координат. б) 4.1.3.29 Зміна кількості руху механічної системи зумовленасилами, що діють на систему. б) – “тільки зовнішніми”;
4.1.3.30 Якщо головний вектор зовнішніх сил, що діють на систему, дорівнює нулеві б) – “не зміниться”;
4.1.3.31 Якщо головний вектор зовнішніх сил, що діють на систему _____________, то кількість руху механічної системи не зміниться. а) – “дорівнює нулеві”;
4.1.3.32 Вкажіть правильні вирази закону збереження б) Якщо
4.1.3.33 Якщо проекція головного вектора зовнішніх сил, що діють на систему, на деяку вісь, то проекція кількості руху системи на дану вісь не зміниться. б) – “дорівнює нулеві”;
4.1.3.34 Якщо проекція головного вектора зовнішніх сил, що діють на систему, на деяку вісь дорівнює нулеві, то проекція кількості руху системи на дану вісь ___________. в) – “не зміниться”;
4.1.3.35 Вкажіть правильні вирази закону збереження кількості руху механічної системи по осі абсцис. а) Якщо Теорема Ейлера 4.1.4.1 Сума векторів секундних кількостей руху рідини, що протікає через два поперечні перерізи труби, які нап-равлені у середину виділеного об’єму, а також головних векторівсил, дорівнює нулеві. в) – “об’ємних і поверхневих”;
4.1.4.2 Вкажіть правильний запис формули Ейлера для дослідження руху суцільного середовища. д)
4.1.4.3 Вкажіть правильні записи формули Ейлера для дослідження руху суцільного середовища в проекціях на декартові осі координат.
4.1.4.4 Вкажіть правильні записи формули Ейлера для дослідження руху суцільного середовища в проекціях на декартові осі координат.
4.2 Теорема про рух центра мас механічної системи
4.2.1 Центр мас механічної системи рухається як матеріальна точка, в якій зосереджена вся маса системи і до якої прикладені всі __ сили, що діють на систему. б) – “зовнішні”;
4.2.2 Центр мас механічної системи ____________, в якій зосереджена вся маса системи і до якої прикладені всі зовнішні сили, що діють на систему. б) – “рухається як матеріальна точка”; 4.2.3 Вкажіть правильну формулу теореми про рух центра мас механічної системи. д)
4.2.4 Вкажіть правильну формулу теореми про рух центра мас механічної системи. д)
4.2.5 Вкажіть правильну формулу теореми про рух центра мас механічної системи. б) 4.2.6 Вкажіть правильну формулу теореми про рух центра мас механічної системи (маса системи не змінюється з часом). а) 4.2.7 Вкажіть правильні формули теореми про рух центра мас механічної системи в проекціях на декартові осі координат. в)
4.2.8 Вкажіть правильні формули теореми про рух центра мас механічної системи в проекціях на декартові осі координат. б) 4.2.9 На рух центра мас механічної системи впливають тільки _____________ сили, що діють на систему. б) – “зовнішні”; 4.2.10 Якщо головний вектор б) – “дорівнює нулеві”; 4.2.11 Якщо головний вектор б) – “незалежно від початкових умов”; 4.2.12 Якщо головний вектор б) – “рівномірно і прямолінійно”; 4.2.13 Вкажіть правильний вираз збереження руху центра мас системи. а) Якщо 1) якщо 2) якщо 4.2.14 Якщо проекція головного вектора зовнішніх сил, що діють на систему, на деяку вісьто проекція швидкості центра мас на цю вісь не змінюється, тобто є інтегралом руху. а) – “дорівнює нулеві”;
4.2.15 Вкажіть правильний вираз в проекції на вісь Ох закону збереження руху центра мас системи. в) Якщо 1) якщо 2) якщо 4.2.16 Вкажіть правильний вираз в проекції на вісь Оу закону збереження руху центра мас системи. б) Якщо 1) якщо 2) якщо
Закон площ
4.3.4.1 Секторною швидкістю
4.3.4.2 Вектор секторної швидкості
4.3.4.3 Вкажіть правильний вираз секторної швидкості
4.3.4.4 Напрям вектора секторної швидкості б) – “перпендикулярний”;
4.3.4.5 Момент кількості руху матеріальної точки відносно деякого центра дорівнює _______ відносно даного центра. б) – “подвійному добутку маси точки на її секторну швидкість”;
4.3.4.6 Вкажіть правильний вираз моменту кількості руху матеріальної точки відносно деякого центра, записаний з врахуванням секторної швидкості. а) 4.3.4.7 Центральною силою називають силу, що напрямлена _______________. б) – “до деякого центра О ”;
4.3.4.8 Рух матеріальної точки під дією центральної сили
4.3.4.9 Рух матеріальної точки під дією центральної сили
2. Під дією центральної сили точка рухається зі сталою секторною швидкістю (закон площ) (див. рис.). а) Оскільки
4.3.5 Момент кількості руху (кінетичний момент) механічної системи відносно центра та осі
4.3.5.1 Моментом кількості руху (кінетичним моментом або головним моментом кількості руху) механічної системи відносно деякого центра називають___________суму моментів кількості руху всіх матеріальних точок системи відносно даного центра. б) – “геометричну”;
4.3.5.2 Вкажіть правильну формулу моменту кількості руху (кінетичного моменту, або головного моменту кількості руху) механічної системи відносно деякого центра. б) 4.3.5.3 Моментом кількості руху (кінетичним моментом) механічної системи відносно деякої осі називають __________ суму моментів кількостей руху всіх точок системи відносно даної осі. в) – “алгебраїчну”;
4.3.5.4 Вкажіть правильну формулу моменту кількості руху (кінетичного моменту, або головного моменту кількості руху) механічної системи відносно осі Оz.
4.3.5.5 Вкажіть правильний рисунок, який відповідає моменту кількості руху (кінетичному моменту, або головному моменту кількості руху) механічної системи відносно деякого центра О.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.165.234 (0.014 с.) |

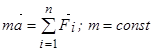 ;
; ;
; ;
;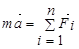 ;
;
 ;
; ;
; .
.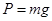 ;
; системи сил, що діють на матеріальну точку”;
системи сил, що діють на матеріальну точку”;
 ;
; , заданої координатним способом визначення її руху.
, заданої координатним способом визначення її руху.
 .
.
 ;
; ;
; .
. ;
; .
.
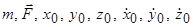 .
.



 і проекції вектора швидкості
і проекції вектора швидкості 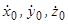 ”.
”. ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; і
і  .
. ;
; ;
;
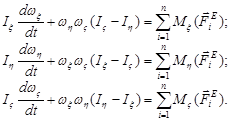
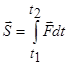 ;
; ;
; .
. .
. .
. ;
; i
i  .
. ;
;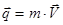 ;
;
 ;
; ;
; ;
; ;
; ;
; ;
;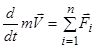 .
. ;
; .
. ;
; ;
;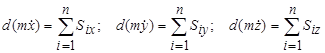 ;
; .
. ;
; ;
; ;
; ;
; ;
;
 ;
; ;
;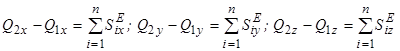 ;
; , то кількість руху механічної системи _____________.
, то кількість руху механічної системи _____________. , то
, то  ;
; , то
, то  ;
; .
.

 .
. .
. ;
; ;
; ;
; ;
; зовнішніх сил, що діють на систему,, то центр мас її залежно від початкових умов рухається рівномірно і прямолінійно або не змінює свого положення.
зовнішніх сил, що діють на систему,, то центр мас її залежно від початкових умов рухається рівномірно і прямолінійно або не змінює свого положення. зовнішніх сил, що діють на систему, дорівнює нулеві, то центр мас їїрухається рівномірно і прямолінійно або не змінює свого положення.
зовнішніх сил, що діють на систему, дорівнює нулеві, то центр мас їїрухається рівномірно і прямолінійно або не змінює свого положення. , то
, то  ; при цьому:
; при цьому: , то
, то  , тобто, центр мас руха-
, тобто, центр мас руха- , то
, то  , тобто, центр мас системи не змінює свого положення.
, тобто, центр мас системи не змінює свого положення. , то
, то  ; при цьому:
; при цьому: , то
, то  , тобто, центр мас по осі Ох рухається рівномірно;
, тобто, центр мас по осі Ох рухається рівномірно; , то
, то  , тобто, центр мас системи по осі Ох не змінює свого положення.
, тобто, центр мас системи по осі Ох не змінює свого положення. , то
, то  ; при цьому:
; при цьому: , то
, то  , тобто, центр мас по осі Оу рухається рівномірно.
, тобто, центр мас по осі Оу рухається рівномірно. , то
, то  , тобто, центр мас системи по осі Оу не змінює свого положення.
, тобто, центр мас системи по осі Оу не змінює свого положення. називають фізичну величину, яка дорівнює швидкості зміни ______, що описує радіус-вектор точки, в даний момент часу.
називають фізичну величину, яка дорівнює швидкості зміни ______, що описує радіус-вектор точки, в даний момент часу.
 точки дорівнює ____________ добутку радіуса-вектора рухомої точки на вектор її лінійної швидкості.
точки дорівнює ____________ добутку радіуса-вектора рухомої точки на вектор її лінійної швидкості.
 ;
;
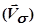 ________ до площини секторної площі
________ до площини секторної площі  і напрямлений в той бік, щоб з кінця цього вектора було видно рух точки К проти обертання годинникової стрілки.
і напрямлений в той бік, щоб з кінця цього вектора було видно рух точки К проти обертання годинникової стрілки.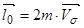 ;
; відбувається по ________ траєкторії і точка рухається зі сталою секторною швидкістю (закон площ).
відбувається по ________ траєкторії і точка рухається зі сталою секторною швидкістю (закон площ).
 відбувається по плоскій траєкторії і точка рухається зі ____________ швидкістю (закон площ).
відбувається по плоскій траєкторії і точка рухається зі ____________ швидкістю (закон площ).
 , то
, то 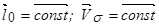 ;
; ;
; ;
;




