
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Д-3 Дослідження руху матеріальної точки, що знаходиться під дією постійних силСодержание книги
Поиск на нашем сайте
Мета роботи Засвоїти методику експериментального визначення горизонтальної дальності польоту тіла; набути навиків в роботі з вимірювальними приладами і оцінювання похибки досліду.
Прилади і приладдя Експериментальна установка (рис. Д3.1) Набір тіл із різних матеріалів. Секундомір. Кутомір. Лінійка.
Опис установки Установка (рис. Д3.1) складається з площини АВ, яка може бути установлена під будь-яким кутом до горизонту. По площині рухається тіло М, яке з швидкістю
Теоретичні відомості Тіло М рухається з точки А (рис. Д3.1) з початковою швидкістю Розглянемо рух тіла М, вважаючи його материальною точкою. На тіло діють такі сили: У відповідності з основним законом динаміки, маємо:
Проектуючи обидві частини рівності на вісь
або
Із рівняння (Д3.1) при
або
Інтегруючи рівняння (Д3.2), знаходимо
враховуючи, що (Д3.3) будемо мати: Інтегруючи (Д3.4), отримуємо
Знаходимо сталі інтегрування. Приймаючи до уваги положення сис-теми координат, ставимо початкові умови і знаходимо сталі інтегрування. Для координати х1 маємо Врахуємо, що початкова швидкість точки Таким чином:
В момент часу
Розв’язуючи отриману систему, знаходимо: Розглянемо рух точки М на дільниці ВС. На точку діє тільки сила тяжіння
Проектуючи це рівняння на осі x і y, з початком в точці В, отримуємо диференціальні рівняння руху точки:
Інтегруючи систему диференціальних рівнянь (Д3.7) аналогічно рів-нянню (Д3.1), маємо:
Початкові умови руху тіла на ділянці ВС:
Підставляючи значення цих умов в (Д3.8) та (Д3.9), знаходимо сталі інтегрування
Рівняння руху приймають вигляд
Момент падіння
або
Розв’язуючи систему, одержану з рівнянь (Д3.6) та (Д3.10), знаходимо:
Порядок виконання роботи 1. Перевірити горизонтальність положення платформи АВ, далі нахилити її під таким кутом 2. Для відмітки місця падіння тіла на горизонтальну площину (точка С), поряд з приладом встановити ящик з плоскою резиною, на яку пос- 3. Установити тіло на похилій площині на відстані 4. За допомогою лінійки виміряти величину h=ВД та d=ДЕ (висоту та дальність польоту). 5. Дослід провести 6 разів при незмінній довжині 6. Обчислити теоретичні значення величини дальності
7. Результат занести в таблицю Д 3.1
Таблиця Д 3.1
8. Визначити похибки вимірювань.
Контрольні запитання Запишіть диференціальні рівняння руху матеріальної точки в проекціях на декартові та натуральні осі координат. Які обмеження накладаються на початкові умови руху точки та сили для того, щоб вона рухалась рівномірно і прямолінійно?
Д-4 Визначення коефіцієнта тертя ковзання за допомогою похилої площини
Мета роботи Визначити експериментально коефіцієнти тертя спокою і руху для тіл із різних матеріалів.
Прилади та приладдя 1. Експериментальна установка (рис. Д4.1). 2. Набір тіл із різних матеріалів. 3. Кутомір. 4. Ватерпас. 5. Секундомір. 6. Лінійка
Опис установки Установка (рис. Д4.1) складається з площини ОО1, яка може бути вста-новлена під довільним кутом до горизонту. На площині встановлюється тіло А у формі паралелепіпеда. Площина ОО1 може обертатися навколо шарніра О.
Теоретичні відомості
На тіло діють такі сили: G — сила ваги тіла, N —нормальна реакція площини; F — сила тертя тіла на площині. В граничному випадку рівноваги тіла сила тертя має максимальне значення F=f×N. де f — коефіцієнт тертя спокою. Рівняння рівноваги тіла:
звідки де При подальшому збільшенні кута Сила тертя при русі: F=f1×N1 де f1 — середнє значення коефіцієнта тертя при русі. Нехай тіло ковзає по площині і переміщується на деяку відстань l1 за час t1. Згідно з теоремою про зміну кількості руху матеріальної точки в проекціях на вісь х маємо:
Проекція на вісь Ох імпульсу постійних сил, що діють на тіло (матеріальну точку) запишеться у вигляді:
Початкова швидкість тіла
Підставляючи записані вирази в рівняння (Д4.1), маємо:
Після інтегрування цього виразу, одержуємо:
Розв’язуючи останній вираз відносно
Порядок виконання роботи 1. Перевірити по ватерпасу і відрегулювати горизонтальне положення платформи. 2. Для визначення коефіцієнта тертя спокою до горизонту, при якому починає зразок ковзати, а також визначити коефіцієнт тертя спокою. Дослід виконати з усіма зразками, що виготовлені з різних матеріалів. 3. Порівняти одержані результати з табличними (табл. Д4.1).
Таблиця Д4.1
4. Для визначення коефіцієнта 5. Зразок встановити на площині на відстані
Таблиця Д4.2
6. Дати можливість зразку рухатись по похилій площині. Визначити час руху зразка 7. Дослід повторити з різними матеріалами. 8. Оцінити абсолютну та відносу похибки експериментальнх дослідів. 9. Результати дослідів та обчислень занести в таблицю Д4.3. Таблиця Д4.3
Контрольні запитання 1. Сформулювати закони тертя ковзання при спокої. 2. Як направлена сила тертя при русі тіла? 3. За якю формулою визначається сила тертя при русі? 4. Як зміниться коефіцієнт тертя при русі взалежності від швидкості руху тіла? Від яких факторів стану тіла залежить коефіцієнт тертя?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.250 (0.011 с.) |

 покидає площину і падає в точку С горизонтальної площини.
покидає площину і падає в точку С горизонтальної площини. по дільниці АВ шорсткої площини, яка складає з горизонтом кут
по дільниці АВ шорсткої площини, яка складає з горизонтом кут  . Коефіцієнт тертя тіла по площині
. Коефіцієнт тертя тіла по площині  . В точці В тіло залишає площину з швидкістю
. В точці В тіло залишає площину з швидкістю  в точку С горизонтальної площини. Треба визначити відстань
в точку С горизонтальної площини. Треба визначити відстань  .
. - сили ваги;
- сили ваги;  - сила тертя;
- сила тертя;  - нормальна реакція поверхні.
- нормальна реакція поверхні.
 , направлену вздовж лінії руху точки, отримуємо диференціальне рівняння руху:
, направлену вздовж лінії руху точки, отримуємо диференціальне рівняння руху:
 (Д 3.1)
(Д 3.1) отримаємо:
отримаємо: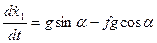
 (Д 3.2)
(Д 3.2)
 (Д3.3)
(Д3.3) , то розділяючи змінні в рівнянні
, то розділяючи змінні в рівнянні (Д3.4)
(Д3.4)
 , звідки
, звідки 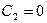 .
. , тому отри-муємо
, тому отри-муємо  .
. ;
; (Д3.5)
(Д3.5) точка залишає дільницю АВ, тобто
точка залишає дільницю АВ, тобто  ,
, 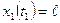 або
або ;
;  (Д3.6)
(Д3.6)
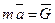

 (Д3.7)
(Д3.7) (Д3.8)
(Д3.8) (Д3.9)
(Д3.9)
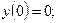
 ,
, 
 ,
,  ,
,  ,
, 
 ,
,  (Д3.10)
(Д3.10) відповідає умовам
відповідає умовам ,
, 



 від краю. Відпустити тіло та виміряти секундоміром час
від краю. Відпустити тіло та виміряти секундоміром час  проходження ділянки АВ похилої площини.
проходження ділянки АВ похилої площини. та
та  .
. , використовуючи замість t його середню величину
, використовуючи замість t його середню величину  , де n = 6.
, де n = 6. , см
, см
 , с
, с
 , см
, см
 Площина ОО1 (рис. Д4.1) обертається навколо осі, що проходить через О, і її можна встановити під довільним кутом до горизонту. На площині покладено тіло масою m. Визначимо найбільший кут
Площина ОО1 (рис. Д4.1) обертається навколо осі, що проходить через О, і її можна встановити під довільним кутом до горизонту. На площині покладено тіло масою m. Визначимо найбільший кут  , при якому тіло А буде залишатись у рівновазі на площині.
, при якому тіло А буде залишатись у рівновазі на площині. ;
; 
 ;
; 

 — кут тертя.
— кут тертя. (Д4.1)
(Д4.1)
 , а проекція швидкості точки на вісь ОХ:
, а проекція швидкості точки на вісь ОХ: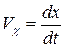



 одержуємо:
одержуємо: .
. установити на пла-тформу зразок. Збільшуючи нахил платформи, визначати кут нахилу
установити на пла-тформу зразок. Збільшуючи нахил платформи, визначати кут нахилу  , більшим ніж відповідний для нього кут тертя спокою
, більшим ніж відповідний для нього кут тертя спокою  .
.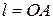 від шарніра О. (табл. Д4.2).
від шарніра О. (табл. Д4.2). та відстань
та відстань  . Дослід повторити 6 раз і обчислити середнє арифметичне значення
. Дослід повторити 6 раз і обчислити середнє арифметичне значення 




