
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальні рівняння руху вільної матеріальноїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Динаміка точки Динаміка - розділ теоретичної механіки, що вивчає механічний рух матеріальних об’єктів (матеріальної точки, системи матеріальних точок, твердого тіла) під дією прикладених до них сил та з урахуванням їх мас. 3.1. Закони динаміки (Ньютона) Перший (закон інерції): ізольована матеріальна точка перебуває в стані спокою або прямолінійного рівномірного руху доти, доки вплив зовнішніх сил не виведе її з цього стану. Другий (основний закон динаміки): сила, що діє на матеріальну точку, надає їй прискорення, яке пропорційне величині сили і має напрям сили: Третій (закон рівності дії та протидії): дві матеріальні точки взаємодіють між собою з силами, рівними за величиною і протилежними за напрямом: Четвертий закон динаміки (закон незалежності дії сил): якщо на матеріальну точку одночасно діють декілька сил, то прискорення, одержуване точкою, дорівнює геометричній сумі прискорень, які точка одержує від кожної сили зокрема. Диференціальні рівняння руху вільної матеріальної Точки Основне рівняння динаміки:
де
Дане рівняння можна подати у вигляді проекцій на три осі декартових координат х,у,z (алгебраїчна форма):
де Диференціальні рівняння руху матеріальної точки в натуральній формі:
де Дві задачі динаміки перша абопряма задача динаміки точки - рух точки, а також її маса, відомі. Треба знайти силу, яка діє на точку. Друга або обернена задача динаміки точки - відомі сили, що діють на точку, її маса, а також початкові умови руху. Треба визначити закон руху точки. Розв'язання першої задачі - знаходження сили за даним законом руху матеріальної точки зводиться до знаходження прискорення точки. Розв'язання другої задачі - знаходження закону руху матеріальної точки за даними силами пов'язане з інтегруванням диференціальних рівнянь руху. Загальний розв'язок цих рівнянь визначає координати точки як функції часу і сталих інтегрування.
Початкові умови - величини, що визначають положення точки (її координати) і проекції вектора швидкості на осі координат у деякий фіксований момент часу
Розв’язання: 1) складемо диференціальне рівняння руху матеріальної точки:
2) після інтегрування диференціального рівняння отримаємо:
де С 1, С 2 - сталі інтегрування; 3) визначимо сталі інтегрування за допомогою початкових умов при t = 0:
4) закону руху визначимо у вигляді:
Кінематичне збудження коливань При кінематичному збудженні коливань вантажу заданий рух здійснює основа у точці В прикріплення до нього вільного кінця пружини за законом Для консервативної системи диференційне рівняння коливань вантажу буде:
або
Вантаж буде здійснювати при заданих початкових умовах рух за законом
або
Приклади розв’язання задач по дослідженню Загальні теореми динаміки точки Терема про зміну моменту кількості руху Матеріальної точки Момент кількості руху матеріальної точки відносно центра О є вектором, що дорівнює векторному добуткові радіуса - вектора точки, початок якого є в точці О, на кількість руху цієї точки
Теорема про зміну моменту кількості руху матеріальної точки: похідна за часом від моменту кількості руху матеріальної точки відносно нерухомого центра О дорівнює моменту рівнодійної сил, прикладених до цієї точки, відносно того ж центра
В проекціях на осі прямокутної системи координат теорему можна записати у вигляді трьох рівнянь:
Отже похідна за часом від моменту кількості руху матеріальної точки відносно нерухомої осі дорівнює моменту рівнодійної сили відносно тієї ж осі.
3.6. Принцип Даламберадля матеріальної точки Сила інерції матеріальної точки
При русі точки по кривій силу інерції можна подати як суму двох складових:
де
Принцип Даламбера для невільної матеріальної точки: при русі матеріальної точки активні сили і реакції в'язей, а також сила інерції матеріальної точки, якщо її умовно прикласти, являють собою зрівноважену систему сил:
де
Системи Кінетична енергія механічної системи - це скалярна величина, яка дорівнює сумі кінетичних енергій матеріальних точок системи:
де Теорема Кеніга. Кінетична енергія системи дорівнює сумі кінетичної енергії центра мас системи і кінетичної енергії системи в її відносному русі по відношенню до системи координат, яка рухається поступально разом з центром мас:
де
де М - маса тіла, Теорема про зміну кінетичної енергії механічної системи: - у диференціальній формі: диференціал кінетичної енергії механічної системи дорівнює сумі елементарних робіт зовнішніх і внутрішніх сил, прикладених до точок системи:
- в інтегральній формі: зміна кінетичної енергії системи матеріальних точок на певному переміщенні дорівнює сумі робіт зовнішніх і внутрішніх сил на тому самому переміщенні:
де Робота сили, прикладеної до твердого тіла, що обертається навколо нерухомої осі
де У випадку сталого моменту Елементарна робота сил, прикладених до твердого тіла, що вільно рухається, дорівнює сумі роботи головного вектора
Потужність
де 4.5. Принцип Даламбера для механічної системи Принцип Даламбера для матеріальної системи: при русі системи матеріальних точок геометрична сума головних векторів активних сил, реакцій в'язей і сил інерції дорівнює нулю; геометрична сума головних моментів активних сил, реакцій в'язей і сил інерції відносно деякого нерухомого О центра дорівнює нулю:
Сили інерції тіла приводяться:
- при обертальному русі до головного моменту сил інерції
- при плоскопаралельному русі - до головного вектора сил інерції
4.6. Елементи аналітичної механіки 4.6.1. Класифікація в’язей Розрізняють вільні й невільні механічні системи. Механічна система називається вільною, якщо рух її точок необмежений ніякими сторонніми тілами (в'язами). Якщо рух механічної системи обмежений в’язами, то вона називається невільною. Класифікація в'язей. Обмеження, які в'язі накладають на механічну систему, аналітично виражаються у вигляді співвідношень (рівнянь або нерівностей) між часом, координатами і швидкостями матеріальних точок, що утворюють систему. Геометричні (скінченні) в'язі — це такі в'язі, до рівняння яких не входять швидкості точок системах:
Кінематичні (диференціальні) в'язі - це такі в'язі, до рівняння яких входять швидкості точок системи:
Якщо рівняння кінематичної в'язі після інтегрування можна перетворити у рівняння геометричної в'язі, то така кінематична в'язь називається голономною (інтегрованою). У протилежному випадку кінематична в'язь називається неголомною (неінтегрованою). Стаціонарні в'язі - це в'язі, до рівнянь яких час не входить у явному вигляді. Нестаціонарні в'язі — це в'язі, до рівнянь яких час входить у явному вигляді. Двобічні (утримуючі) в'язі — це в'язі, що обмежують рух точок механічної системи у двох взаємно протилежних напрямах зовнішніх нормалей до поверхні в'язі. 0днобічні (неутримуючі) в'язі — це в'язі, що обмежують рух точок механічної системи в якомусь одному напрямі зовнішньої нормалі до поверхні в'язі і не обмежують його в протилежному напрямі. Утримуючі в'язі аналітично виражаються рівнянням
а неутримуючі - нерівностями
Принцип можливих переміщень Можливими (або віртуальними) переміщеннями системи називаються умовні нескінченно малі її незалежні переміщення, що дозволяються в'язами системи в даний момент часу (в даному положенні системи). Ідеальні в'язи — це такі в'язі, сума робіт реакцій яких на будь-якому можливому переміщенні системи дорівнює нулю:
Приклади ідеальних в’язей: абсолютно гладенька поверхня (напрямні); ідеальні шарніри (підшипник), стержні та ін. Принцип можливих переміщень: для рівноваги системи зі стаціонарними двобічними ідеальними в'язями необхідно і достатньо, щоб сума елементарних робіт усіх активних сил, діючих на систему, на будь-якому можливому переміщенні системи з даного її положення рівноваги дорівнювала нулю:
або в скалярній формі або в аналітичній формі 4.6.3. Узагальнені координати, швидкості та узагальнені сили. Узагальненими координатами Похідні за часом від узагальнених координат, тобто величини Обчислимо роботу прикладених до точок системи активних сил
де Величини Щоб обчислити узагальнену силу Маємо Якщо активні сили є потенціальними то узагальнені сили дорівнюватимуть частинним похідним від потенціальної енергії П (q1, q2,…, qs) по узагальнених координатах:
Рівняння динаміки системи. Загальне рівняння При русі системи, підпорядкованої голономним двостороннім ідеальним в'язям, сума робіт активних сил і сил інерції на будь-якому можливому переміщенні системи повинна дорівнювати нулю:
або де Рівняння Лагранжа II роду мають такий вигляд:
де Т - кінетична енергія системи, представлена як функція узагальнених координат, узагальнених швидкостей і часу; Удар Удар - явище, при якому швидкості точок тіла за дуже малий (близький до нуля) проміжок часу змінюються на скінченну величину. ударні сили - сили, при дії яких відбувається удар. Ударні сили діють протягом дуже малого проміжку часу і досягають дуже великих значень. В теорії удару в якості міри взаємодії розглядають не самі ударні сили, а їх імпульси. Ударний імпульс - вектор, який визначається за формулою
де t - тривалість удару. Теорема про зміну кількості руху матеріальної точки при ударі (основне рівняння теорії удару матеріальної точки): зміна кількості руху матеріальної точки під час удару дорівнює геометричній сумі ударних імпульсів, які діють на точку:
де Коефіцієнт відновлення при ударі:
де Окремі випадки: 1) К = 1 - абсолютно пружний удар (тіла, що співударяються, після удару мають різні швидкості); 2) К = 0 - абсолютно непружний удар (тіла, що співударяються, після удару рухаються як одне тіло). Теорема про зміну кількості руху механічної системи при ударі: зміна кількості руху системи під час удару дорівнює геометричній сумі усіх зовнішніх ударних імпульсів, які діють на систему:
де Теорема про зміну моменту кількості руху механічної системи при ударі: зміна головного моменту кількості руху системи відносно нерухомого полюса А під час удару дорівнює геометричній сумі моментів усіх зовнішніх ударних імпульсів відносно того ж полюса:
де Удар називається центральним, якщо нормаль до поверхонь тіл, що співударяються, в точці їх дотику (лінія удару) проходить через центри мас цих тіл. Удар називається прямим, якщо швидкості тіл, що співударяються, напрямлені по лінії удару. В протилежному випадку удар називається косим. Основні рівняння прямого центрального удару:
де Теорема Остроградського-Карно:
де У випадку косого удару мають місце рівняння
де Додаток 1 Завдання для роботи “Визначення реакцій опор системи тіл” Конструкція складається з двох тіл. Визначити реакцію опор А і В, а також тиск у проміжному шарнірі С. Методика розв’язання задач розглянута у роз- ділі 1.7.
Додаток 2 Завдання для роботи “Кінематичний аналіз плоского механізму” Визначити для заданого положення механізму швидкість і прискорення точки В і С, а також кутову швидкість і кутове прискорення ланки, до якої належить точка С. Схеми механізмів наведені на наступних сторінках, а необхідні для розрахунку розміри і кінематичні параметри представлені у таблиці, де
Додаток 3 Методика розв’язання задач та завдання для роботи “дослідження коливального руху матеріальної точки” Розв’язання задач завдання слід проводити в такій послідовності: - визначити тип механічної системи, вид схеми з’єднання пружних елементів вихідної схеми, вид коливального руху вантажу, а також засіб збудження його коливань; - перетворити (у випадку необхідності) вихідну схему в розрахункову з одним пружним елементом, показати на розрахунковій схемі вісь Ох, і напрямок кінематичного збудження - розрахувати еквівалентну жорсткість - визначити, враховуючи тип механічної системи, вид коливального руху вантажу та засіб збудження його коливань, закон руху вантажу у загальному вигляді (для цього використати формули розділу 3.4), розрахувати коефіцієнти та параметри закону руху для конкретної
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1917; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.208.191 (0.016 с.) |

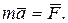

 - можна записати у вигляді диференціального рівняння (векторна форма):
- можна записати у вигляді диференціального рівняння (векторна форма):
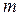 – маса точки;
– маса точки; - радіус-вектор точки, який є функцією часу.
- радіус-вектор точки, який є функцією часу.  ;
;  ;
; 


 - алгебраїчні суми проекції всіх сил, що діють на точку, на координатні осі.
- алгебраїчні суми проекції всіх сил, що діють на точку, на координатні осі.


 - проекція швидкості на дотичну;
- проекція швидкості на дотичну;  - радіус кривизни траєкторії в даній точці;
- радіус кривизни траєкторії в даній точці; 

 - алгебраїчні суми проекцій сил, що діють на точку, на натуральні осі
- алгебраїчні суми проекцій сил, що діють на точку, на натуральні осі  . Цими рівняннями зручно користуватися, коли точка рухається, наприклад, по колу.
. Цими рівняннями зручно користуватися, коли точка рухається, наприклад, по колу. (звичайно
(звичайно  ,
,  ,
,  ,
,  ,
,  ,
, 
 Приклад: матеріальна точка масою m рухається по прямій у напрямку осі Ох під дією сталої сили
Приклад: матеріальна точка масою m рухається по прямій у напрямку осі Ох під дією сталої сили  . Знайти закон руху точки при початкових умовах
. Знайти закон руху точки при початкових умовах ,
,
 .
.

 , або
, або 
 ;
;
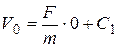 Þ
Þ 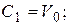
 Þ
Þ 
 .
. .
.










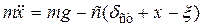 ,
або
,
або  ,
або
,
або  ,
де
,
де  .
Закон вимушених коливань вантажу має вигляд
.
Закон вимушених коливань вантажу має вигляд
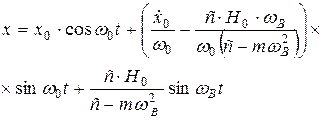 (12)
(12)



 або
або 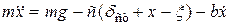 або
або  або
або  де
де  .
.
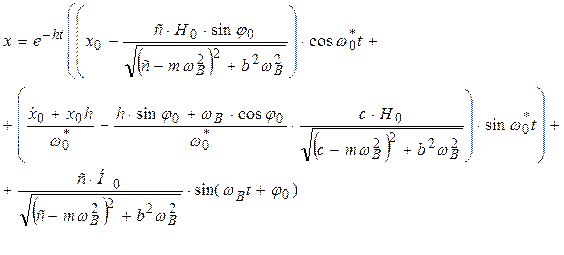 (13)
(13) де
де 

 - початкова фаза;
- початкова фаза; 


 Момент кількості руху матеріальної точки відносно координатної осі:
Момент кількості руху матеріальної точки відносно координатної осі:
 .
.





 за величиною дорівнює добутку маси точки на величину її прискорення і напрямлена протилежно вектору прискорення точки
за величиною дорівнює добутку маси точки на величину її прискорення і напрямлена протилежно вектору прискорення точки


 ,
,
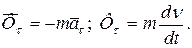
 ,
, - рівнодійна активних сил;
- рівнодійна активних сил;  - рівнодійна реакцій в'язей;
- рівнодійна реакцій в'язей; 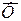 - сила інерції точки.
- сила інерції точки.
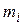 - маса і - тої точки системи,
- маса і - тої точки системи,  - її швидкість.
- її швидкість. ,
,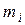 - маса і -тої точки системи;
- маса і -тої точки системи; 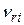 - відносна швидкість точки по відношенню до центра мас;
- відносна швидкість точки по відношенню до центра мас;  - маса всієї системи;
- маса всієї системи;  - швидкість центра мас системи. Кінетична енергія твердого тіла визначається за формулами:
- швидкість центра мас системи. Кінетична енергія твердого тіла визначається за формулами:


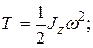


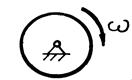

 ,
,

 - швидкість центра мас тіла;
- швидкість центра мас тіла;  - момент інерції тіла відносно осі z (вісь обертання) або осі z, що проходить через центр мас;
- момент інерції тіла відносно осі z (вісь обертання) або осі z, що проходить через центр мас;  - кутова швидкість тіла.
- кутова швидкість тіла.

 і
і  - кінетична енергія системи в кінці і на початку шляху;
- кінетична енергія системи в кінці і на початку шляху;  - сума робіт зовнішніх сил;
- сума робіт зовнішніх сил;  - сума робіт внутрішніх сил.
- сума робіт внутрішніх сил. , дорівнює добутку моменту сили відносно даної осі на кут повороту тіла:
, дорівнює добутку моменту сили відносно даної осі на кут повороту тіла:
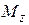
 - момент сили відносно осі;
- момент сили відносно осі;  - елементарний і певний кут повороту тіла.
- елементарний і певний кут повороту тіла. отримаємо
отримаємо 
 полюса О і роботи головного моменту
полюса О і роботи головного моменту  цієї системи сил відносно полюса на елементарному обертальному переміщенні:
цієї системи сил відносно полюса на елементарному обертальному переміщенні:
 є фізичною величиною, що характеризує швидкість, з якою виконується робота
є фізичною величиною, що характеризує швидкість, з якою виконується робота
 - швидкість точки прикладення сили,
- швидкість точки прикладення сили,  - проекція сили на дотичну,
- проекція сили на дотичну,  - момент сили відносно осі обертання,
- момент сили відносно осі обертання,  - кутова швидкість тіла. За одиницю потужності прийнято Вт
- кутова швидкість тіла. За одиницю потужності прийнято Вт 


 :
:
 яка прикладена у центрі мас;
яка прикладена у центрі мас;


 та головного вектора сил інерції
та головного вектора сил інерції 





 , який прикладений до центра мас, та головного моменту сил інерції
, який прикладений до центра мас, та головного моменту сил інерції  :
:



 - прискорення центра мас тіла;
- прискорення центра мас тіла;  - кутове прискорення обертального руху;
- кутове прискорення обертального руху;  - моменти інерції тіла відносно осі обертання
- моменти інерції тіла відносно осі обертання  та осі
та осі 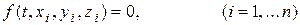 .
.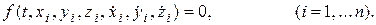







 називають такі незалежні один від одного параметри, заданням яких можна однозначно визначити положення усіх точок системи. Такими параметрами можуть бути декартові координати, кути, віддалі та ін. Число
називають такі незалежні один від одного параметри, заданням яких можна однозначно визначити положення усіх точок системи. Такими параметрами можуть бути декартові координати, кути, віддалі та ін. Число  цих незалежних параметрів називають числом ступенів вільності механічної системи.
цих незалежних параметрів називають числом ступенів вільності механічної системи. , називаються узагальненими швидкостями системи.
, називаються узагальненими швидкостями системи. на можливому переміщенні системи:
на можливому переміщенні системи:

 , що є множниками при можливих (віртуальних) переміщеннях узагальнених координат у формулі роботи активних сил на можливому переміщенні системи, називаються узагальненими силами.
, що є множниками при можливих (віртуальних) переміщеннях узагальнених координат у формулі роботи активних сил на можливому переміщенні системи, називаються узагальненими силами. досить надати можливе переміщення координаті
досить надати можливе переміщення координаті  і визначити роботу
і визначити роботу  активних сил на переміщеннях точок системи, які зумовлені тільки зміною координати
активних сил на переміщеннях точок системи, які зумовлені тільки зміною координати  .
.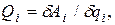


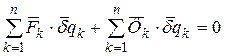

 - сила інерції точки;
- сила інерції точки;  - узагальнена сила інерції;
- узагальнена сила інерції;  - можливе переміщення точки.
- можливе переміщення точки.
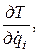
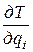 - частинні похідні кінетичної енергії по узагальнених швидкостях і координатах.
- частинні похідні кінетичної енергії по узагальнених швидкостях і координатах.

 - швидкості точки після і до удару відповідно.
- швидкості точки після і до удару відповідно. , 0 ≤ к ≤ 1,
, 0 ≤ к ≤ 1, ,
,  - модулі нормальних складових відносної швидкості точки торкання тіл після і до удару відповідно.
- модулі нормальних складових відносної швидкості точки торкання тіл після і до удару відповідно.
 - кількість руху системи після і до удару відповідно.
- кількість руху системи після і до удару відповідно.
 - головні моменти кількості руху системи відносно полюса А після і до удару відповідно.
- головні моменти кількості руху системи відносно полюса А після і до удару відповідно.

 - проекції швидкості тіл до удару на вісь х, що співпадає з лінією удару;
- проекції швидкості тіл до удару на вісь х, що співпадає з лінією удару;  - проекції швидкості тіл на вісь х після удару;
- проекції швидкості тіл на вісь х після удару;  - маси тіл;
- маси тіл;  - коефіцієнт відновлення.
- коефіцієнт відновлення.
 - втрата кінетичної енергії двох тіл при ударі;
- втрата кінетичної енергії двох тіл при ударі;  - кінетичні енергії системі до і після удару відповідно;
- кінетичні енергії системі до і після удару відповідно; 
 - втрачені швидкості.
- втрачені швидкості.

 і
і  - проекції швидкостей тіл на вісь п, що проходить через центри мас цих тіл до удару і після нього.
- проекції швидкостей тіл на вісь п, що проходить через центри мас цих тіл до удару і після нього.


 - кутова швидкість і кутове прискорення кривошипа ОА для заданого положення механізму;
- кутова швидкість і кутове прискорення кривошипа ОА для заданого положення механізму; 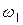 - кутова швидкість колеса І (стала);
- кутова швидкість колеса І (стала);  - швидкість і прискорення точки А. Кочення коліс відбувається без ковзання. Методика розв’язання задач розглянута у розділі 2.5.2.
- швидкість і прискорення точки А. Кочення коліс відбувається без ковзання. Методика розв’язання задач розглянута у розділі 2.5.2. ,
рад/с
,
рад/с
 ,
рад/с2
,
рад/с2
 ,
см/с
,
см/с
 ,
см/с2
,
см/с2



 , силу ваги
, силу ваги  вантажу, сили пружності
вантажу, сили пружності 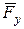 та опору
та опору  ) руху (точки О 1 на осі Ох), статичну деформацію
) руху (точки О 1 на осі Ох), статичну деформацію  пружини під дією вантажу;
пружини під дією вантажу; пружини, враховуючи вид схеми з’єднання пружних елементів вихідної схеми, і величину статичної деформації
пружини, враховуючи вид схеми з’єднання пружних елементів вихідної схеми, і величину статичної деформації  і
і  для вантажу, знайти, враховуючи тип механічної системи, частоти
для вантажу, знайти, враховуючи тип механічної системи, частоти  або
або  (для дисипативної системи) вільних коливань вантажу, коефіцієнт h системи;
(для дисипативної системи) вільних коливань вантажу, коефіцієнт h системи;


