
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кінематичне збудження коливаньСодержание книги Поиск на нашем сайте
При кінематичному збудженні коливань вантажу заданий рух здійснює основа у точці В прикріплення до нього вільного кінця пружини за законом Для консервативної системи диференційне рівняння коливань вантажу буде:
або
Вантаж буде здійснювати при заданих початкових умовах рух за законом
або
Приклади розв’язання задач по дослідженню Коливального руху матеріальної точки Приклад 1. Знайти рівняння коливального руху вантажу D у напрямку осі Ох з моменту дотику ним плити, вважаючи, що при подальшому русі вантаж від плити не відділяється. Плита, яка займає в стані спокою горизонтальне положення, є невагомою. Рухи плити та основи вважати поступальними. Умови задачі. Пролетівши без початкової швидкості відстань
Перетворимо вихідну механічну схему в розрахункову з одним пружним елементом який має еквівалентну жорсткість се=с1+с2. На рис. точка О на осі Ох визначає положення статичної рівноваги вантажу, точка О 1 − положення вантажу D в момент дотику плити,
Величина статичної деформації
Визначаємо значення власної частоти
Закон руху вантажу визначаємо формулою (12) розділу 3.4:
Перевірка: При Відповідь: Вантаж здійснює двочастотні коливання за законом Приклад 2. Знайти рівняння коливального руху вантажу D по гладенькій похилій площині у напрямку осі Ох, що співпадає з віссю пружини. Умова задачі. Система встановлених на пружині вантажів D (
пружини зрівноважує не всю силу ваги вантажу
Закон руху вантажу визначаємо за виразом (5) розділу 3.4.2:
Перевірка: При Відповідь: Вантаж здійснює одночастотні затухаючі коливання за законом х = Загальні теореми динаміки точки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 .
.










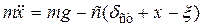 ,
або
,
або  ,
або
,
або  ,
де
,
де  .
Закон вимушених коливань вантажу має вигляд
.
Закон вимушених коливань вантажу має вигляд
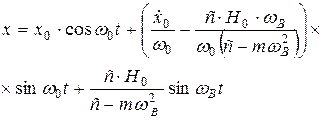 (12)
(12)



 або
або 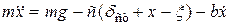 або
або  або
або  де
де  .
.
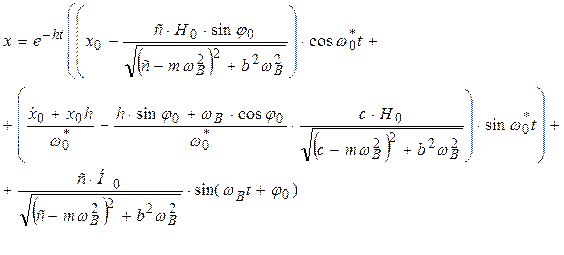 (13)
(13) де
де 

 - початкова фаза;
- початкова фаза; 

 0,2 м, вантаж D (
0,2 м, вантаж D ( 20 кг) з’єднується у момент часу
20 кг) з’єднується у момент часу  з плитою, яка зв’язує систему двох недеформованих паралельно закріплених пружин, які мають коефіцієнти жорсткості та опору с 1 = 100 Н/см, с 2 = 200 Н/см,
з плитою, яка зв’язує систему двох недеформованих паралельно закріплених пружин, які мають коефіцієнти жорсткості та опору с 1 = 100 Н/см, с 2 = 200 Н/см,  0. Одночасно основа починає здійснювати рух за законом
0. Одночасно основа починає здійснювати рух за законом  (см).
(см).

 - статична деформація
- статична деформація


 під дією вантажу,
під дією вантажу, 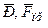 - відповідно сила ваги вантажу та сила пружності пружини, x - напрямок кінематичного збудження в точці В кріплення пружини до рухомої основи.
Знаходимо еквівалентну жорсткість:
- відповідно сила ваги вантажу та сила пружності пружини, x - напрямок кінематичного збудження в точці В кріплення пружини до рухомої основи.
Знаходимо еквівалентну жорсткість:
 = 100 + 200 =300 Н/см =
= 3×104 Н/м.
= 100 + 200 =300 Н/см =
= 3×104 Н/м.

 і початкових умов
і початкових умов  :
: ,
, м,
м, .
.

 (м).
(м). м, що співпадає з величиною раніше визначеної початкової умови
м, що співпадає з величиною раніше визначеної початкової умови  .
.
 (м).
(м). 1 кг) знаходиться в положенні статичної рівноваги. У момент часу
1 кг) знаходиться в положенні статичної рівноваги. У момент часу  м/с у напрямку позитивного відліку координати х. Коефіцієнти жорсткості та опору пружини дорівнюють с = 2·104 Н/м,
м/с у напрямку позитивного відліку координати х. Коефіцієнти жорсткості та опору пружини дорівнюють с = 2·104 Н/м,  1,5 Н×с/м. Прийняти кут
1,5 Н×с/м. Прийняти кут  .
.


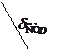








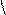

















 - відповідно сила ваги вантажу D, сили пружності та опору пружини, точка А - положення вантажу D у момент зняття вантажу Е.
В даній схемі в положенні статичної рівноваги вантажу D (точка О) сила пружності
- відповідно сила ваги вантажу D, сили пружності та опору пружини, точка А - положення вантажу D у момент зняття вантажу Е.
В даній схемі в положенні статичної рівноваги вантажу D (точка О) сила пружності 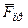
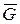 , а тільки її складову
, а тільки її складову 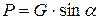 у напрямку осі Ох, яка співпадає з віссю пружини Знайдемо величину статичної деформації
у напрямку осі Ох, яка співпадає з віссю пружини Знайдемо величину статичної деформації  пружини, коефіцієнт демпфування h системи, власні частоти
пружини, коефіцієнт демпфування h системи, власні частоти  , а також початкову умову
, а також початкову умову 
 м;
м;  ;
; ,
, .
.

 м, що співпадає з величиною раніше визначеної початкової умови
м, що співпадає з величиною раніше визначеної початкової умови  (м).
(м).


