
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямолінійні коливання матеріальної точкиСодержание книги
Поиск на нашем сайте
Механічні рухи, які періодично повторюються, називаються механічними коливаннями. При цьому на матеріальну точку можуть діяти поновлюючі сили (сили, що намагаються повернути точку в положення рівноваги), сила опору руху, яка залежить від швидкості точки, та зовнішня збурююча сила. рух точки здійснюється по прямій, співпадаючої з сумісною лінією дії вказаних сил. Залежно від комбінації цих сил розрізняють наступні види коливального руху. 3.4.1. Вільні коливання, які відбуваються під дією тільки поновлюючої сили, величина якої пропорційна відхиленню матеріальної точки від положення її статичної рівноваги.
вантаж 1 нерухомий, координата Тому диференціальні рівняння руху вантажу приймають вигляд
або де Закон коливань вантажу в цьому випадку буде
де амплітуда і початкова фаза коливань точки. У відповідності з (4) вантаж (матеріальна точка) здійснює гармонічний коливальний рух. Розглянута на рисунку механічна система називається консервативною. Пружини, які з’єднують вантаж з основою, можуть утворювати систему паралельно, послідовно і паралельно-послідовно (змішано) з’єднаних пружних елементів. У цьому випадку подані на рисунках вихідні механічні
а при змішаному з’єднанні
або або де Характер руху вантажу істотним чином залежить від співвідношення h і
де Відповідно рисунку механічна система називається дисипативною, а рух вантажу має затухаючий коливальний характер. При цьому амплітуда коливань При
де
Це рівняння описує аперіодично затухаючий рух. Координата х вантажу при Гранично аперіодичний рух (граничний випадок) має місце при
де Розглянутий рух (7) також є аперіодичним затухаючим ( 3.4.3. Вимушені коливання у випадку, коли збурююча сила Силове збудження коливань При силовому збудженні коливань збурююча сила
Закон коливання вантажу:
або де Характер руху вантажу істотно залежить від співвідношення величин Якщо У випадку близькості частоти збурюючої сили до частоти власних коливань (
Такий рух називається биттям: коливальних рух, який відбувається з частотою При співпаданні частоти збурюючої сили з власною частотою
З часом амплітуда вимушених коливань вантажу безмежно зростає. Таке
або або де При заданих початкових умовах
або де
Коливання вантажу є двочастотними: вони відбуваються одночасно як з частотою
При
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |




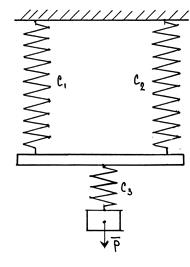
 Механічна схема, яка моделює вільні прямолінійні коливання вантажу (матеріальної точки) масою m у напрямку осі Ох показана на рис., де 1 - вантаж; 2 - пружина; 3 - нерухома основа. Тут:
Механічна схема, яка моделює вільні прямолінійні коливання вантажу (матеріальної точки) масою m у напрямку осі Ох показана на рис., де 1 - вантаж; 2 - пружина; 3 - нерухома основа. Тут:  - довжина недеформованої пружини;
- довжина недеформованої пружини;  - статична деформація пружини під дією вантажу; х - поточна координата вантажу відносно положення статичної рівноваги при його русі;
- статична деформація пружини під дією вантажу; х - поточна координата вантажу відносно положення статичної рівноваги при його русі;  - сила ваги (
- сила ваги ( ;
;  - сила пружності пружини, яка є різновидністю поновлюючої сили
- сила пружності пружини, яка є різновидністю поновлюючої сили  де
де  - повна деформація пружини; с - коефіцієнт жорсткості (пружності) пружини; точка О - положення статичної рівноваги
- повна деформація пружини; с - коефіцієнт жорсткості (пружності) пружини; точка О - положення статичної рівноваги
 (1)
або
(1)
або  , (2)
де
, (2)
де  - прискорення вантажу.
У положенні статичної рівноваги
- прискорення вантажу.
У положенні статичної рівноваги
 , а сила ваги (
, а сила ваги ( зрівноважується силою пружності пружини, яка дорівнює
зрівноважується силою пружності пружини, яка дорівнює  .
.
 , (3)
, (3) - кругова (циклічна, власна) частота коливань вантажу (матеріальної точки).
- кругова (циклічна, власна) частота коливань вантажу (матеріальної точки). , (4)
, (4) ,
,  - постійні інтегрування;
- постійні інтегрування;  - початкові умови (початкове положення і початкова швидкість вантажу на момент розгляду руху, тобто при
- початкові умови (початкове положення і початкова швидкість вантажу на момент розгляду руху, тобто при  );
);  ,
,  -
-

 , при послідовному з’єднанні
, при послідовному з’єднанні  ,
,
 .
.


 3.4.2. Вільні коливання матеріальної точки при наявності сил опору. При русі в середовищі (рідина), а також при деформації реальних пружин на матеріальну точку діє сила опору, яку при малих швидкостях руху можна вважати прямо пропорційною швидкість точки:
3.4.2. Вільні коливання матеріальної точки при наявності сил опору. При русі в середовищі (рідина), а також при деформації реальних пружин на матеріальну точку діє сила опору, яку при малих швидкостях руху можна вважати прямо пропорційною швидкість точки:  , де b - коефіцієнт опору руху.
, де b - коефіцієнт опору руху.
 або
або  ,
,
 ,
, ,
, - коефіцієнт демпфування коливань;
- коефіцієнт демпфування коливань;  .
. . Закон коливання вантажу у випадку малого опору (h <
. Закон коливання вантажу у випадку малого опору (h <  , (5)
, (5)
 ;
;  ;
;  .
. з часом спадає за експоненціальним законом до нуля.
з часом спадає за експоненціальним законом до нуля. (випадок великого опору) закон коливань вантажу буде мати вигляд
(випадок великого опору) закон коливань вантажу буде мати вигляд , (6)
, (6) ;
;  ;
; ;
;  .
. монотонно зменшується, а вантаж наближається до положення статичної рівноваги.
монотонно зменшується, а вантаж наближається до положення статичної рівноваги. . Тут закон руху вантажу буде
. Тут закон руху вантажу буде , (7)
, (7) .
. при
при  ).
). змінюється за гармонійним законом.
змінюється за гармонійним законом. прикладена безпосередньо до матеріальної точки (вантажу).
прикладена безпосередньо до матеріальної точки (вантажу).

 ;
;  ;
;  .
Диференціальне рівняння руху вантажу має вигляд
.
Диференціальне рівняння руху вантажу має вигляд
 або
або  ,
або
,
або  .
або
.
або  , де
, де 
 (8)
(8) ,
, ;
;  ;
;  ;
;  (частоти збурюючої сили).
(частоти збурюючої сили). або
або  , то закон коливань вантажу бігармонійний (двочастотний). Відбувається накладення вільних коливань консервативної механічної системи на її коливання з частотою збурюючої сили. При цьому амплітуда і початкова фаза вільних коливань вантажу залежить одночасно і від початкових умов
, то закон коливань вантажу бігармонійний (двочастотний). Відбувається накладення вільних коливань консервативної механічної системи на її коливання з частотою збурюючої сили. При цьому амплітуда і початкова фаза вільних коливань вантажу залежить одночасно і від початкових умов  збурюючої сили, і від механічних характеристик m, с самої системи.
збурюючої сили, і від механічних характеристик m, с самої системи. ), виникає явище биття, при якому закон коливань вантажу (8) перетворюється, наприклад, при нульових початкових умовах
), виникає явище биття, при якому закон коливань вантажу (8) перетворюється, наприклад, при нульових початкових умовах  на вигляд
на вигляд . (9)
. (9) ) функцією часу.
) функцією часу. вантаж коливається за законом
вантаж коливається за законом . (10)
. (10)

 ;
;  ;
;  та
та  (випадок малого опору) диференціальне рівняння руху вантажу має вигляд.
(випадок малого опору) диференціальне рівняння руху вантажу має вигляд.
 або
або 
 ,
, ,
, .
. (11)
(11)
 ;
; 
 ;
;  ;
; ;
; .
. вільних коливань дисипативної системи, так і з частотою
вільних коливань дисипативної системи, так і з частотою  у першому доданку призводить до швидкого затухання коливального руху вантажу з частотою
у першому доданку призводить до швидкого затухання коливального руху вантажу з частотою  і зсувом фаз
і зсувом фаз  , величини яких визначаються конкретним значенням частоти
, величини яких визначаються конкретним значенням частоти  , а параметри механічної систем задовольняють нерівності
, а параметри механічної систем задовольняють нерівності  , де
, де  - відносне демпфування, то амплітуда вимушених коливань вантажу буде найбільшою:
- відносне демпфування, то амплітуда вимушених коливань вантажу буде найбільшою: .
. .
.


