
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кінематика матеріальної точки. Радіус-вектор, вектори переміщення швидкості і прискорення.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кінематика матеріальної точки. Радіус-вектор, вектори переміщення швидкості і прискорення. Кінематика точки - розділ кінематики, що вивчає математичний опис руху матеріальних точок. Основним завданням кінематики є опис руху за допомогою математичного апарату без з'ясування причин, що викликають цей рух. Положення точки визначається набором узагальнених координат - впорядкованим набором числових величин, повністю описують положення тіла. У самому простому випадку це координати точки (радіус-вектора) у вибраній системі координат. Матеріальна точка - тіло, розмірами якого в порівнянні з характерними відстанями даної задачі можна знехтувати. Так Землю можна вважати Матеріальною Точкою (М.Т.) при вивченні її руху навколо Сонця, кулю можна вважати М. Т. при її русі в полі тяжіння Землі, але не можна вважати такою при обліку її обертового руху в стовбурі гвинтівки. Радіус-вектор - вектор, який визначає положення М.Т. в просторі:
Оборотні і необоротні процеси. Циклічні процеси. Цикл Карно та його коефіцієнт корисної дії. Постулати II начала термодинаміки. Поняття про ентропію, математичне формулювання II начала термодинаміки. Статистичне тлумачення II начала термодинаміки. Межі його застосування. Теорема Карно: Термічний ККД оборотнього циклу Карно не залежить від властивостей робочого тіла і виражається формулою ηк = (Tн – Тх)/Тн. Термічний ККД необоротного циклу Карно завжди менший термічного ККД оборотнього циклу Карно, який здійснюється між тими ж температурами Tн та Тх: ηк необор < ηк обор. Термічний ККД довільного оборотнього циклу не перевищує термічного ККД оборотнього циклу Карно: ηобор ≤ ηк обор = (Tн – Тх)/Тн. У замкненій (ізольованій) системі ентропія зростає або є сталою: ΔS ≥ 0, TdS ≥ dU + pdV. Відомо з означення ентропії, що при зміні стану ізольованої системи зміна її ентропії дорівнює нулеві, якщо всі процеси оборотні, або більша від нуля, якщо в системі мають місце необоротні процеси. Якщо необоротні процеси в ізольованій системі відбуваються постійно, то ентропія даної системи весь час зростає, і її енергія безперервно знецінюється (деградує). За деякий час наступає момент, коли ентропія стає максимальною, тоді вся внутрішня енергія стає повністю знеціненою і ні в якій мірі не зможе перейти в інші види енергії. Цикл Карно. Тепловий двигун – це пристрій, який перетворює внутрішню енергію палива в механічну. Енергія, яка виділяється під час згорання палива, через теплообмін передається газу. Газ, розширюючись, виконує роботу проти зовнішніх сил і приводить у рух механізм. Для того щоб двигун працював циклічно, газ стискається, віддаючи теплоту холодильнику (навколишньому середовищу). Робоче тіло двигуна дістає кількість теплоти ΔQн від нагрівника, виконує роботу А над зовнішніми тілами і передає кількість теплоти ΔQх холодильнику. Оскільки система після закінчення циклу повертається до початкового стану, зміна внутрішньої енергії дорівнює нулю (ΔU = 0) і за першим законом термодинаміки ΔА = ΔQн–ΔQх, де ΔА - механічна робота, яку виконує газ, ΔQн - кількість теплоти, одержаної від нагрівника, ΔQх - кількість теплоти, переданої холодильнику. Величина η: η = (ΔQн–ΔQх)/ΔQн = ΔА/ΔQн називається коефіцієнтом корисної дії (ККД) теплової машини. З усіх теплових машин, які працюють з нагрівником, що має температуру Тн, і холодильником, що має температуру Тх, найбільший коефіцієнт корисної дії має теплова машина, що працює за циклом Карно, який складається з двох ізотерм і двох адіабат. Існують декілька еквівалентних формулювань другого початку термодинаміки:Постулат Клаузіуса: «Неможливий процес, єдиним результатом якого була б передача тепла від більш холодного тіла до більш гарячого (такий процес називається процесом Клаузіуса). Постулат Томсона (Кельвіна): «Неможливий круговий процес, єдиним результатом якого було б виробництво роботи за рахунок охолодження теплового резервуара» (такий процес називається процесом Томсона). Інше формулювання другого початку термодинаміки грунтується на понятті ентропії:«Ентропія ізольованої системи не може зменшуватися» (закон неспадання ентропії).Таке формулювання грунтується на уявленні про ентропії як про функції стану системи, що також має бути постульовано. 29. Реальні гази. Відхилення властивостей газів від ідеальності. Експериментальні ізотерми реального газу. Рівняння стану неідеального газу (рівняння Ван-дер-Ваальса з експериментальними ізотермами). Критичний стан речовини. Критичні параметри. Закони ідеальних газів описують реальні гази. Газ Ван-дер-Ваальса – це модель реального газу, в якій молекули розглядаються як тверді кульки певного об’єму (діаметром d), між якими діють сили взаємного притягання. Наявність власного розміру кульок зумовлює те, що в даній моделі враховано і сили відштовхування між молекулами реального газу. [p + (m/μ)2∙a/V2][V - (m/μ)∙b] = RT-рівняння Ван-дер-Ваальса. Рівняння стану реального газу відрізняється від рівняння Клапейрона-Менделєєва введенням двох поправок: 1. Врахування розмірів молекул та сил відштовхування між ними. b = 4V0∙N, [b] = м3/моль. Поправка b – поправка Ван-дер-Ваальса на власний об’єм молекул (чисельно дорівнює чотирьом об’ємам всіх молекул в даному об’ємі газу). 2. Врахування сил притягання між молекулами. Вводиться поправка на додатковий внутрішній тиск, який зумовлений притяганням молекул: Δр = а/V2, [a] = (Па∙м6)/моль2 = (Н∙м4)/моль2, де а – коефіцієнт Ван-дер-Ваальса, який залежить від хімічної природи газу. 1. Вода (Н2О) а = 0,5464 (Н∙м4)/моль2; b =0,305∙10-4 м3/моль. 2. Кисень (О2) а = 0,1370 (Н∙м4)/моль2; b = 0,318∙10-4 м3/моль. 3. Водень (Н2) а = 0,0244 (Н∙м4)/моль2; b = 0,266∙10-4 м3/моль. 30. Властивості рідкого стану. Поверхневий шар рідини. Поверхневий натяг (формула Лапласа). Змочування. Капілярні явища Властивості: 1. Спільне та відмінне між рідинами та тв. тілами і газами. У твердому агрегатному стані речовини молекули (атоми) розміщуються, як відомо, впритул одна до одної. Потенціальна енергія взаємодії молекул значно більша від їх кінетичної енергії. 2. Поверхневий натяг рідин. Коефіцієнтом поверхневого натягу називатимемо відношення сили поверхневого натягу Fпов до довжини лінії L, що обмежує поверхню розділу: σ = Fпов/L. 3. Поверхнева енергія рідини. Якщо під дією сил поверхневого натягу зменшується площа поверхневого шару рідини, енергія цього шару теж зменшується. При цьому сили поверхневого натягу виконують роботу, що дорівнює за модулем і протилежна за знаком зміні енергії поверхневого шару ΔE: A = - ΔE = - σΔS, де ΔS - зміна площі поверхневого шару рідини; σ- коефіцієнт поверхневого натягу. З останнього рівняння знаходимо: σ = А/ΔS. [σ] = Дж/м2 = Н/м. 4. Явище змочування та незмочування рідини. Коли поверхневий шар рідини межує з твердим тілом, то взаємодію молекул рідини і твердого тіла слід враховувати. Якщо взаємодія молекул рідини менша, ніж їх взаємодія з молекулами контактного твердого тіла, то маємо випадок змочування і навпаки, коли ця взаємодія більша - незмочування. Інтенсивність змочування характеризується кутом змочування Θ, який утворюється між дотичною до поверхні рідини і поверхнею твердого тіла. Відлік кута виконують у бік рідини. Якщо 0≤Θ<π/2 - поверхня тіла змочувана, а якщо π/2<Θ≤π - незмочувана. 5. Капілярні явища. Явище змочування і незмочування виявляється у піднятті і спусканні рідини в тонких трубках (капілярах). Розглянемо капілярні явища. Опустимо в рідину густиною ρ капіляр радіусом r. Нехай рідина змочує стінки капіляра вздовж поверхні розділу "рідина - стінки - пара". По дотичній в кожній її точці будуть діяти сили поверхневого натягу. Рівнодійна цих сил напрямлена вгору і буде піднімати рідину в капілярі. Підняття рідини в капілярі припиниться тоді, коли сила тяжіння піднятого стовпа рідини зрівноважить силу поверхневого натягу: Fпов = Fтяж. Підставляючи значення поверхневої сили та сили тяжіння отримаємо наступне співвідношення: 2πRσ∙cosΘ = ρgh∙πR2. З останньої рівності знаходимо висоту підняття рідини в циліндричному капілярі: h = (2σ∙cosΘ)/ρgR, де h - висота підняття рідини в циліндричному капілярі; σ - коефіцієнт поверхневого натягу рідини; ρ - густина рідини; R - радіус капіляра; g - прискорення вільного падіння. Саме в капілярах відбуваються основні процеси, пов'язані з диханням і живленням організмів. Часто капілярні явища використовують і в побуті. Застосування рушників, серветок, гігроскопічної вати, марлі, промокального паперу можливе завдяки наявності в них капілярів.
31. Загальна характеристика твердого стану. Аморфні і кристалічні тіла. Дальній порядок в кристалах. Класифікація кристалів за типом кристалічної ґратки. Анізотропія кристалів. Дефекти кристалів Аморфні речовини — твердотільні речовини, які не мають далекого порядку в розташуванні атомів. Прикладами аморфних речовин є скло, пластик. Аморфність твердих тіл ковалентної природи (наприклад, полімерів) пояснюється великою ентропією ланцюгів. Аморфні речовини тз часом кристалізуються, проте процес кристалізації при кімнатних температурах може тривати багато років, століть чи навіть тисячоліть. Аморфні речовини не мають чітко визначеної температури плавлення. При нагріванні вони розм'якають. Температура, яка характеризує цей процес називається температурою склування. Криста́л — тверде тіло з упорядкованою внутрішньою будовою, що має вигляд багатогранника з природними плоскими гранями: впорядкованість будови полягає у певній повторюваності у просторі елементів кристала (атомів, молекул, йонів), що зумовлює виникнення т.зв. кристалічної ґратки. Завдяки подібній будові кристалічні речовини мають характерні властивості, як: стала температура плавлення,спайність,анізотропія, пружністьРечовини, що не мають кристалічної ґратки, називають аморфними речовинами. Дальній порядок - упорядкованість у взаємному розташуванні атомів або молекул в речовині (у рідкому або твердому стані), яка (на відміну від ближнього порядку) повторюється на необмежено великих відстанях.Далеким порядком в розташуванні атомів або молекул володіють, наприклад, кристали (квазікристали). Класифікація ґраток за симетрією: Сингонії: 1. триклінна сингонія — найменша симетрія, немає однакових кутів, немає вісей однакової довжини; 2. моноклінна сингонія — два прямих кути, немає вісей однакової довжини; 3. ромбічна сингонія — три прямих кута (тому ортогонально), немає вісей однакової довжини; 4. гексагональна сингонія — дві вісі однакової довжини в одній площині під кутом 120°, третя вісь під прямим кутом; 5. Тетрагональна сингонія — дві вісі однакової довжини, три прямих кута; 6. тригональна сингонія — три вісі однакової довжини і три рівних непрямі кути; 7. кубічна сингонія — найвища ступінь симетрії, три вісі однакової довжини під прямим кутом. Анізотропі́я — відмінність властивостей середовища у різних напрямках (на відміну від ізотропії). Щодо одних властивостей середовище може бути ізотропним, щодо інших — анізотропним. Може різнитися також ступінь анізотропії. Це явище характерне для показника заломлення світла, діелектричної сталої, теплопровідності, магнітних властивостей кристалів, проникності порід і т. і. Виявляється в кристалах низької симетрії та рідких кристалах. Дефекти у кристалах - підрозділяються на мікродефекти (порушення періодичності в розташуванні атомів, йонів та молекул у кристалічній структурі) і макродефекти (тріщини). Підрозділяються на точкові, лінійні, площинні (двомірні) та об’ємні. Дефекти суттєво впливають на фізичні властивості кристалів, зокрема їхню пластичність, в’язкість, пружність та міцність.
Класифікація. При фазових переходах першого роду поглинається або виділяється прихована теплота. Фазові переходи другого роду відбуваються без поглинання чи виділення тепла. Така сучасна класифікація дещо відрізняється від класифікації Еренфеста, який назвав фазовими переходами першого роду переходи, при яких стрибком міняються перші похідні від вільної енергії, а фазовими переходами другого роду ті, при яких стрибком міняються, відповідно другі похідні від вільної енергії. Інші, відмінні від вільної енергії термодинамічні потенціали, наприклад, внутрішня енергія або ентальпія при фазових переходах першого роду міняються стрибком. Недоліком класифікації Еренфеста є те, що при деяких фазових переходах похідні від вільної енергії прямують до нескінченності, наприклад теплоємність при фазовому переході до феромагнітного стану. Співвідно́шення Кла́узіуса — Клапейро́на — рівняння, яке задає закон залежності тиску від температури на кривій співіснування фаз.
Властивості В основному стані ферміони займають якомога нижчі енергетичні рівні. Накладена принципом виключення Паулі заборона призводить до того, що при нульовій тепературі, коли реалізується основний стан, усі найнижчі одноферміонні рівні зайняті. Найвищий зайнятий у такому стані рівень називається рівнем Фермі. Функція розподілу має вигляд сходинки При збільшенні температури, існує певна ймовірність того, що ферміони системи матимуть енергію, вищу за енергію рівня Фермі. Завдяки цьому існує відмінна від нуля ймовірність того, що рівень із енергією нижчою за енергією рівня Фермі, стане вільним. Чим вища тепература, тим пологішою стає крива розподілу. При дуже високих температурах розподіл Фермі — Дірака переходить у класичний розподіл Максвелла — Больцмана. Стати́стика Бозе — Ейнштейна — розподіл за енергією часток, які належать до бозонів. За розподілом Бозе — Ейнштейна ймовірність того, що в квантовомеханічній багаточастинковій системі існує бозон у одночастинковому квантовому стані
Оскільки ймовірність повинна бути додатним числом, значення хімічного потенціалу завжди менше за енергію основного стану бозонів. Якщо кількість бозонів строго визначена (N), то хімічний потенціал визначається із умови нормування розподілу. Фізична природа Квантові частки бозони відрізняються від частинок класичної фізики тим, що їх принципово неможливо розрізнити. Крім того, хвильова функція бозонів завжди симетрична відносно перестановок частинок. Це призводить до зміни кількості можливих станів. Наприклад, розглянемо систему, у якій можливі два одночастинкові стани
У квантовій фізиці можливі лише три стани:
Таким чином, у найпростішому випадку, за однакової енергії станів, ймовірність реалізації конкретного стану у класичній фізиці дорівнює 1/4, а у квантовій фізиці — 1/3. При розгляді великого числа частинок і одночастинкових станів для цих частинок, для ймовірності заповнення стану отримують наведену вище формулу розподілу Бозе — Ейнштейна. Доведення можна знайти у підручниках із статистичної фізики, наведених у джерелах. Наслідки Одним із наслідків квантової статистики Бозе — Ейнштейна є можливість існування у тривимірних системах за низьких теператур особливої фази речовини, що складається з бозонів — Бозе-конденсату. Статистиці Бозе — Ейнштейна підкоряється електромагнітне випромінювання, яке перебуває у тепловій рівновазі з тілом. Тому її застосування пояснює спектр випромінювання абсолютно чорного тіла. Застосування статистики Бозе — Ейнштейна дозволило пояснити температурну залежність теплоємності твердого тіла за низьких температур (див. температура Дебая, закон Дебая).
Електрика та магнетизм Гістерезис магнітний.
Однією з основних особливостей сильномагнітних мінералів є залежність їхньої магнітної індукції або намагніченості від напруженості поля. Як показано на рис., первинне намагнічування сильномагнітної речовини відбувається по кривій OAD. При циклічному перемагніченні, що відбувається у напрямку вказаному стрілками, крива намагнічення переходе у криву гістерезису. Крива гістерезису, отримана для умов магнітного насичення, називається граничною петлею. Основні характеристики петлі гістерезису при дослідженнях зразка сильномагнітної речовини в замкненому магнітному ланцюгу: остаточна індукція Br і коерцитивна сила Hc. Остаточна індукція Br свідчить про те, що елементарні струми у феромагнітному тілі при зникненні зовнішнього поля зберегли упорядковану орієнтацію. Коерцитивна сила Hc характеризує величину напруженості поля зворотного напрямку, яку необхідно створити, щоб остаточна індукція зникла і стала рівною нулю. Якщо по осі ординат замість індукції відкласти значення намагніченості Jr, отримуємо петлю гістерезису намагніченості. За цією петлею можна визначити остаточну намагніченість Jr і коерцитивну силу Hc гістерезисної петлі намагнічення. Закон Ома для змінного струму. У випадку змінного струму закон Ома можна розширити, включивши в розгляд також елементи електричного кола, які характеризуються ємністю й індуктивністю. Змінний струм проходить через конденсатор, випереджаючи за фазою напругу. В індуктивності змінний струм відстає за фазою від напруги. Проте в обох випадках амплітуда змінного струму пропорційна амплітуді прикладеної змінної напруги. Математично це можна описати, ввівши комплексні опори (імпеданси). Тоді можна записати Закон Джоуля - Ленца Роботу, яку виконує джерело струму з ЕРС, визначають за формулою: Енергія джерела струму перетворюється частково або повністю у внутрішню енергію провідника або в механічну енергію. Скориставшись законом Ома, роботу можна виразити через силу струму або напругу: Потужність електричного струму дорівнює відношенню роботи А до часу t, протягом якого вона виконується: Одиницею потужності в СІ є Ват (Вт). Якщо по провіднику проходить струм, то провідник нагрівається. Англійський вчений Дж. П. Джоуль і російський вчений Е. Х. Ленц встановили закон (Джоуля – Ленца): кількість теплоти, що виділяється в провіднику зі струмом, пропорційна силі струму, напрузі і часу проходження струму: При відсутності сторонніх сил: Резона́нс — явище сильного зростання амплітуди вимушеного коливання у разі, коли частота зовнішньої сили збігається з власною частотою коливань. Характеристики та опис Резонанс характеризують інтенсивністю, напівшириною спектральної лінії та добротністю. Здебільшого резонанс наближено описують кривою Лоренца
Застосування[ред. • ред. код] Явище резонансу широко використовується в науці й техніці. На ньому ґрунтується робота багатьох радіотехнічних схем та пристроїв, таких як коливні контури. Використовуючи явище резонансу ми вибираємо із багатого різноманіття електромагнітних хвиль в просторі навколо нас саме ті, які відповідають нашій улюбленійрадіостанції, вибираємо телевізійний канал тощо. Проте не завжди резонанс корисний. Відомі випадки, коли навісні мости ламалися при проходжені по ним солдат «в ногу». Це відбувалося через те, що частота власних коливань полотна моста збігалася з частотою ходи людей
47. Контактні явища в металах і напівпровідниках Контактні явища на границі роздягнула напівпровідника й металу. Якщо потенціал виходу для металу менше потенціалу виходу для, то відбувається переважний перехід електронів з металу в напівпровідника, у прикордонному шарі якого виникає збагачений шар. Така границя роздягнула проводить струм в обох напрямках і використовується для конструювання виводів напівпровідникових приладів. Якщо то в границі роздягнула з напівпровідником у металі утвориться шар з негативним зарядом, а в напівпровіднику - збіднений шар з позитивним зарядом. Така границя роздягнула має однобічну провідність. Електричні переходи такого типу називаються по ім'ю вченого, що досліджував їх. Напівпровідникові діоди.. Важливим параметром стабілітронів є температурний коефіцієнт стабілізації напруги, що дорівнює відносній зміні напруги стабілізації при зміні температури на 1 °С и постійному номінальному струмі стабілітрона. Стабілітрони малої потужності з максимально припустимою потужністю втрат використовуються як джерела опорної напруги в компенсаційних стабілізаторах напруги середньої (0,3-0,5 Вт) і великий (понад 8 Вт) потужності - у параметричних стабілізаторах напруги й для обмеження викидів напруги. Останні являють собою прилади, у яких для стабілізації напруги використовуються прямі галузі застосовуються для стабілізації напруги 1 -2 У при струмах до 100 мА.
Світло — хвилі в ефірі Але так як для поширення пружних хвиль потрібна середу, то виникав правомірне питання, в якій же середовищі поширюється світло? Яка середу перебуває на шляху від Сонця до Землі? Прихильники хвильової теорії світла припустили що весь простір у всесвіті заповнено деякої невидимою пружною середовищем. Вони навіть придумали їй назву — світлоносний ефір. У той час, вчені ще не знали про існування яких або хвиль, крім механічних. Такі погляди на природу світла висловлювалися приблизно в 17 столітті. Вважалося, що світло поширюється саме в цьому світлоносного ефіру. Світло — поперечна хвиля Але таке припущення викликало ряд суперечливих питань. До кінця 18 століття було доведено, що світло є поперечною хвилею. А пружні поперечні хвилі можуть виникати тільки в твердих тілах, отже, світлоносний ефір є твердим тілом. Це викликало сильний головний біль у вчених того часу. Як небесні тіла можуть рухатися крізь твердий світлоносний ефір, і при цьому не відчувати жодного опору. Оптика Накладання світових хвиль. Принцип суперпозиції. Когерентність. Інтерференція світла. Одержання когерентних хвиль в оптиці. Двопроменева інтерференція. Поділ фронту хвилі природного джерела світла. Метод Юнга. Дзеркала Френеля. Біпризма Френеля та ін. Інтерфере́нція хвиль — явище накладання двох або більше когерентних світлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум). Результуюча амплітуда А вираховується за формулою: A=
57. Двопроменева інтерференція. Поділ амплітуди світлової хвилі. Інтерференція в плоскопаралельному шарі (смуги однакового нахилу). Інтерференція в клиновидному шарі (смуги рівної товщини, кільця Ньютона) Двопроменева інтерференція. Поділ фронту хвиль. Когерентні хвилі одержуються поділом пучка хвиль. Існують два типии поділу: Хвильового фронту; Амплітуд (за допомогою дзеркала). За допомогою двопроменевої інтерференції вимірюють: оптичну густину речовини; дослідення зміни густини середовища в часі; виміри лінійних зсувів тіл; виміри малих кутових розмірів джерел або відстаней між джерелами; виміри гравітаційної сталої. Смуги інтерференції будуть смугами рівного нахилу, їх спостерігають так само, як і у випадку двопроменевої інтерференції, тобто проектують лінзою на екран, розміщений у фокальній площині лінзи, або користуються зоровою трубою, встановленою на нескінченність. Для характеристики форми контуру інтерференційної смуги введено величину, яка називається різкістю. Різкість інтерференційної смуги визначається відношенням відстані між двома сусідні- ми максимумами до відстані між точками, які лежать з обох боків максимуму, в яких інтенсивність дорівнює половині максимальної величини інтенсивності. Смуги рівної товщини. Допустимо, що товщина пластинки не постійна (∼b, n = const).
Загальні відомості про елементарні частинки. Властивості елементарних частинок. Взаємодія у світі елементарних частинок. Фундаментальні взаємодії. Лептони і адрони. Мезони. Поняття про кварки. Кваркова модель адронів Елемента́рна части́нка — збірний термін, що стосується мікрооб'єктів в суб'ядерному масштабі, які неможливо розщепити на складові частини. Їх будова й поведінка вивчається фізикою елементарних частинок. Поняття елементарних частинок ґрунтується на факті дискретної будови речовини. Інші елементарні частинки є безструктурні й можуть вважатися первинними фундаментальними частинками. За властивостями елементарні частинки поділяють на такі групи: фотони (частинка, що переносить електромагнітну взаємодію), лептони (ферміони, які мають вид точкових частинок аж до масштабів порядку 10−18 м. Не беруть участь в сильних взаємодіях. Участь в електромагнітних взаємодіях експериментально спостерігалася тільки для заряджених лептонів (електрони, мюони) і не спостерігалася для нейтрино), мезони (адрони з цілим спіном, тобто бозони) й баріони (нуклони й гіперони) (адрони з напівцілим спіном, тобто ферміони). Фундамента́льні взаємоді́ї — різні типи взаємодії, що не зводяться одна до одної, елементарних частинок і складених з них тіл. На сьогодні достовірно в
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1075; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.19.136 (0.015 с.) |

 ={
={ 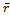 2,
2,  + y
+ y 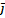 +z
+z  , де i j k - одиничні вектори у напрямку відповідних осей x, y, z. Траєкторією називають уявну лінію, що описує в просторі матеріальна точка при її русі. Відстань між точками відлічувана уздовж траєкторії, називається пройденим шляхом. Пройдений шлях - величина скалярна. Вектор, поведений з початкової точки траєкторії в кінцеву, називається переміщенням ∆
, де i j k - одиничні вектори у напрямку відповідних осей x, y, z. Траєкторією називають уявну лінію, що описує в просторі матеріальна точка при її русі. Відстань між точками відлічувана уздовж траєкторії, називається пройденим шляхом. Пройдений шлях - величина скалярна. Вектор, поведений з початкової точки траєкторії в кінцеву, називається переміщенням ∆ 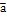 =
= 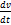 . Оскільки швидкість — похідна по часу від радіус-вектра r рухомої матеріальної точки, то прискорення можна записати, як другу похідну по часу від радіус-вектора:
. Оскільки швидкість — похідна по часу від радіус-вектра r рухомої матеріальної точки, то прискорення можна записати, як другу похідну по часу від радіус-вектора: 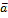 =
=  .
. Рисунок: (Ізотерми реального газу. Область I – рідина, область II – двофазна система «рідина + насичена пара», область III – газоподібна речовина. K – критична точка.). Газ можна перетворити в рідину лише при температурі, нижчій за певне її значення – значення критичної температури. При температурах, вищій за критичну, збільшенням тиску не можна перетворити газ у рідину. Критичні параметри стану Ткр, pкр, Vкр можна виразити через величини а та b газу: Ткр = 8а/(27Rb); pкр = a/(27b2); Vкр = 3b. Критичні температури водяної пари, азоту й кисню відповідно рівні: T(H2O) = 646K, T(N2) = 128K, T(O2) = 155K. Теорія Ван-дер-Ваальса добре описує стан та поведінку реальних газів, що підтверджується експериментальними дослідженнями, проте вона не застосовна для дуже стиснутих газів.
Рисунок: (Ізотерми реального газу. Область I – рідина, область II – двофазна система «рідина + насичена пара», область III – газоподібна речовина. K – критична точка.). Газ можна перетворити в рідину лише при температурі, нижчій за певне її значення – значення критичної температури. При температурах, вищій за критичну, збільшенням тиску не можна перетворити газ у рідину. Критичні параметри стану Ткр, pкр, Vкр можна виразити через величини а та b газу: Ткр = 8а/(27Rb); pкр = a/(27b2); Vкр = 3b. Критичні температури водяної пари, азоту й кисню відповідно рівні: T(H2O) = 646K, T(N2) = 128K, T(O2) = 155K. Теорія Ван-дер-Ваальса добре описує стан та поведінку реальних газів, що підтверджується експериментальними дослідженнями, проте вона не застосовна для дуже стиснутих газів.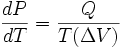 , де P — тиск, T — температура, Q — прихована теплота,
, де P — тиск, T — температура, Q — прихована теплота, 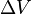 — зміна об'єму речовини при фазовому переході. Формула Клаузіуса — Клапейрона є наслідком рівності хімічних потенціалів різних фаз при фазовому переході.
— зміна об'єму речовини при фазовому переході. Формула Клаузіуса — Клапейрона є наслідком рівності хімічних потенціалів різних фаз при фазовому переході. із енергією
із енергією  визначається формулою
визначається формулою , де
, де  — хімічний потенціал,
— хімічний потенціал,  — стала Больцмана, T — температура.
— стала Больцмана, T — температура.
 і
і 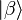 . Для двох таких частинок у класичній фізиці існує 4 можливі стани:
. Для двох таких частинок у класичній фізиці існує 4 можливі стани: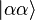 ,
,  ,
, 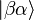 ,
, 
 ,
, 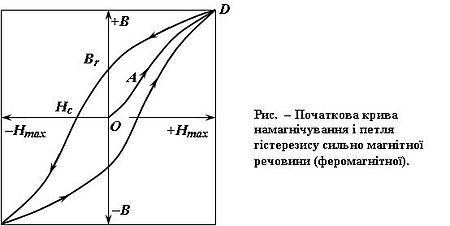

 де U — амплітуда змінної напруги, I — амплітуда змінного струму, Z — імпеданс.
де U — амплітуда змінної напруги, I — амплітуда змінного струму, Z — імпеданс.
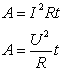
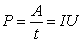


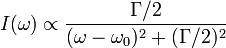 , де ω — частота зовнішньої сили, ω0 — частота власного коливання, Γ — стала затухання, яку називають також шириною лінії. Часто приводиться також γ= Γ/2 — півширина лінії.
, де ω — частота зовнішньої сили, ω0 — частота власного коливання, Γ — стала затухання, яку називають також шириною лінії. Часто приводиться також γ= Γ/2 — півширина лінії.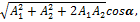 де A1 та A2— амплітуди відповідних хвиль,
де A1 та A2— амплітуди відповідних хвиль,  — різниця фаз цих хвиль. Явище інтерференції використовується, наприклад, в радіотехніці і акустиці для створення складних антен. Когере́нтність — це властивість хвилі зберігати свої частотні, поляризаційні й фазові характеристики. Когере́нтність — корельоване протікання в часі й у просторі декількох випадкових коливальних або хвильових процесів, яке дозволяє одержувати при їхньому додаванні чітку інтерференційну картину. Завдяки когерентності хвиль виникають інтерференційні явища. Відстань, на якій когерентність зберігається, називають довжиною когерентності. Суперпози́ція — накладення різних сутностей. Наприклад, суперпозиція хвиль із різними частотами. У лінійних середовищах хвилі з різними частотами можуть розповсюджуватися незалежно, не впливаючи одна на одну, а тому їхня дія є сумою (суперпозицією) дій окремих хвиль. У випадку близьких частот суперпозиція може призводити до утворення биття. Інтерфере́нція хвиль — явище накладання двох або більше когерентних світлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум). Когерентні хвилі одержуються поділом пучка хвиль. Існують два типии поділу: Хвильового фронту; Амплітуд (за допомогою дзеркала). За допомогою двопроменевої інтерференції вимірюють: оптичну густину речовини; дослідення зміни густини середовища в часі; виміри лінійних зсувів тіл; виміри малих кутових розмірів джерел або відстаней між джерелами; виміри гравітаційної сталої. Метод Юнга. У методі пучок світла спрямовується на непрозорий екран-ширму з двома паралельними прорізами, позаду якого встановлюється проекційний екран. Цей досвід демонструє інтерференцію світла, що є доказом хвильової теорії. Особливість прорізів у тому, що їх ширина приблизно дорівнює довжині хвилі випромінюваного світла. На проекційному екрані можна було б побачити тільки дві паралельних смуги світла, що пройшли через прорізи ширми. Максимум яскравості опиниться там, де згідно нової теорії, яскравість повинна бути практично нульовий. Корпускулярна теорія світла є невірною, коли прорізи досить тонкі, створюючи тим самим інтерференцію. На проекційному екрані виходить цілий ряд чергуються інтерференційних смуг, що й було продемонстровано Томасом Юнгом. Дзеркала Френеля - оптичний пристрій, запропоноване в 1816 О. Ж. Френеля для спостереження явища інтерференції когерентних світлових пучків. Пристрій складається з двох плоских дзеркал I і II, що утворюють двогранний кут, що відрізняється від 180 ° всього на кілька кутових хв. Біпризма Френеля - оптичний пристрій для отримання когерентних світлових пучків, запропоноване Френелем. Джерело розташовується в площині підстав призм. Промені від джерела, що пройшли через кожну з призм, заломлюються, таким чином з'являється два уявних когерентних джерела, і в області перекриття променів цих уявних джерел можливо спостерігати інтерференцію. Двопроменева інтерференція. Поділ фронту хвиль. Когерентні хвилі одержуються поділом пучка хвиль. Існують два типи поділу: Хвильового фронту; Амплітуд (за допомогою дзеркала). За допомогою двопроменевої інтерференції вимірюють: оптичну густину речовини; дослідення зміни густини середовища в часі; виміри лінійних зсувів тіл; виміри малих кутових розмірів джерел або відстаней між джерелами; виміри гравітаційної сталої.
— різниця фаз цих хвиль. Явище інтерференції використовується, наприклад, в радіотехніці і акустиці для створення складних антен. Когере́нтність — це властивість хвилі зберігати свої частотні, поляризаційні й фазові характеристики. Когере́нтність — корельоване протікання в часі й у просторі декількох випадкових коливальних або хвильових процесів, яке дозволяє одержувати при їхньому додаванні чітку інтерференційну картину. Завдяки когерентності хвиль виникають інтерференційні явища. Відстань, на якій когерентність зберігається, називають довжиною когерентності. Суперпози́ція — накладення різних сутностей. Наприклад, суперпозиція хвиль із різними частотами. У лінійних середовищах хвилі з різними частотами можуть розповсюджуватися незалежно, не впливаючи одна на одну, а тому їхня дія є сумою (суперпозицією) дій окремих хвиль. У випадку близьких частот суперпозиція може призводити до утворення биття. Інтерфере́нція хвиль — явище накладання двох або більше когерентних світлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум). Когерентні хвилі одержуються поділом пучка хвиль. Існують два типии поділу: Хвильового фронту; Амплітуд (за допомогою дзеркала). За допомогою двопроменевої інтерференції вимірюють: оптичну густину речовини; дослідення зміни густини середовища в часі; виміри лінійних зсувів тіл; виміри малих кутових розмірів джерел або відстаней між джерелами; виміри гравітаційної сталої. Метод Юнга. У методі пучок світла спрямовується на непрозорий екран-ширму з двома паралельними прорізами, позаду якого встановлюється проекційний екран. Цей досвід демонструє інтерференцію світла, що є доказом хвильової теорії. Особливість прорізів у тому, що їх ширина приблизно дорівнює довжині хвилі випромінюваного світла. На проекційному екрані можна було б побачити тільки дві паралельних смуги світла, що пройшли через прорізи ширми. Максимум яскравості опиниться там, де згідно нової теорії, яскравість повинна бути практично нульовий. Корпускулярна теорія світла є невірною, коли прорізи досить тонкі, створюючи тим самим інтерференцію. На проекційному екрані виходить цілий ряд чергуються інтерференційних смуг, що й було продемонстровано Томасом Юнгом. Дзеркала Френеля - оптичний пристрій, запропоноване в 1816 О. Ж. Френеля для спостереження явища інтерференції когерентних світлових пучків. Пристрій складається з двох плоских дзеркал I і II, що утворюють двогранний кут, що відрізняється від 180 ° всього на кілька кутових хв. Біпризма Френеля - оптичний пристрій для отримання когерентних світлових пучків, запропоноване Френелем. Джерело розташовується в площині підстав призм. Промені від джерела, що пройшли через кожну з призм, заломлюються, таким чином з'являється два уявних когерентних джерела, і в області перекриття променів цих уявних джерел можливо спостерігати інтерференцію. Двопроменева інтерференція. Поділ фронту хвиль. Когерентні хвилі одержуються поділом пучка хвиль. Існують два типи поділу: Хвильового фронту; Амплітуд (за допомогою дзеркала). За допомогою двопроменевої інтерференції вимірюють: оптичну густину речовини; дослідення зміни густини середовища в часі; виміри лінійних зсувів тіл; виміри малих кутових розмірів джерел або відстаней між джерелами; виміри гравітаційної сталої.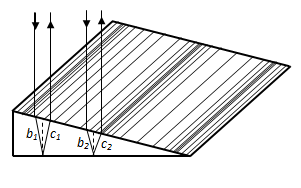 Тоді у всіх тих місцях пластинки, де товщина b, а отже, і різниця ходу Δ однакові, спостерігається той самий результат інтерференції. Це означає, що уздовж якої-небудь темної або світлої інтерференційної смуги, що утворюється на поверхні, товщина цієї пластинки та сама. Смуги рівної товщини локалізовані на поверхні пластинки. При спостереженні в білому світлі смуги будуть пофарбовані так, що поверхня містить усі кольори веселки. Кільця Ньютона - приклад смуг рівної товщини. Вони спостерігаються при відбитті світла. від дотичних одна з одною плоско паралельної товстої скляної пластинки й плоско опуклої лінзи з великим радіусом кривизни. Роль тонкої плівки змінної товщини b, від поверхні якої відбиваються когерентні хвилі, відіграє зазор між пластинкою й лінзою.
Тоді у всіх тих місцях пластинки, де товщина b, а отже, і різниця ходу Δ однакові, спостерігається той самий результат інтерференції. Це означає, що уздовж якої-небудь темної або світлої інтерференційної смуги, що утворюється на поверхні, товщина цієї пластинки та сама. Смуги рівної товщини локалізовані на поверхні пластинки. При спостереженні в білому світлі смуги будуть пофарбовані так, що поверхня містить усі кольори веселки. Кільця Ньютона - приклад смуг рівної товщини. Вони спостерігаються при відбитті світла. від дотичних одна з одною плоско паралельної товстої скляної пластинки й плоско опуклої лінзи з великим радіусом кривизни. Роль тонкої плівки змінної товщини b, від поверхні якої відбиваються когерентні хвилі, відіграє зазор між пластинкою й лінзою.


