

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Задача двох тіл. Закони Кеплера.
Содержание книги
- Кінематика матеріальної точки. Радіус-вектор, вектори переміщення швидкості і прискорення.
- Обертальний рух матеріальної точки. Кутова швидкість та прискорення. Рух точки по колу. Лінійні й кутові величини, їх зв'язок. Рівняння рівномірного і нерівномірного рухів точки по колу.
- Задача двох тіл. Закони Кеплера.
- Механічні коливання. Рух під дією пружних і квазіпружних сил. Рівняння руху найпростіших систем: пружинний, математичний і фізичний маятники. Енергія коливального тіла.
- Коливання в системі з багатьма ступенями вільності. Нелінійні коливання. Параметричний резонанс
- Рух відносно неінерціальних систем відліку
- І начало термодинаміки. Застосування 1-го начала термодинаміки до ізопроцесів. Поняття про теплоємність. Рівняння Майєра. Адіабатичний процес. Рівняння Пуасона.
- Статистична теорія квантових ідеальних газів. Розподіли Фермі – Дірака та Бозе – Ейнштейна.
- Закон Кулона. Напруженість поля. Принцип суперпозицій. Теорема Гауса та її застосування
- Електричне поле в діелектриках
- Дія магнітного поля на рухомий заряд. Сила лоренца. Визначення питомого заряду електрону. Масспектрометр
- Властивості електромагнітних хвиль.
- Електромагнітні хвилі на межі діелектриків. Електромагнітна природа світла.
- Принцип гюйгенса-френеля. Зони френеля. Прямолінійне поширення світла і дифракція. Дифракція френеля на круглому отворі, круглому екрані, від краю напівобмеженої площини
- Фотоелектричний ефект. Квантова теорія фотоефекту. Фотоелементи та їх застосування. Фотонна теорія світла. Характеристики фотона. Дослідне підтвердження корпускулярної природи світла
- Багатоелектронні атоми. Квантові числа, що описують електрон в атомі. Принцип Паулі. Будова атомної оболонки. Періодична система елементів
- Склад ядра та його характеристики: заряд і масове число ядра, енергія зв'язку, дефект маси. Момент кількості руху і магнітний момент ядра. Експериментальні методи ядерної фізики
- Ядерні сили. Моделі атомних ядер
- Радіоактивність. Види радіоактивності. Закони радіоактивного розпаду. Приклади радіоактивних перетворень ядер. Дозиметрія
- Структурування навчального змісту шкільного курсу фізики.
- Формування знань та умінь з фізики.
- Формування вмінь роботи з навчальною літературою з фізики.
- Використання нових інформаційних технологій навчання.
- Навчальний процес “сутність” і “процес” навчання, “явище” і навчальний процес: урок і система уроків.
- Навчальні конференції та семінари з фізики.
- Введення узагальненого уявлення про фізичну величину на перших уроках фізики в 7 класі.
- V. Розв’язується навчальна проблема.
- Способи організації навчальних занять в історії методики навчання фізики.
- Загальні критерії оцінювання навчальних досягнень учнів у системі загальної середньої освіти.
- Методика навчання фізики. Приклади задач методики фізики-науки. Самостійність науки – методика навчання фізики. Методика навчання, як майстерність вчителя. Зв’язок між наукою і практикою.
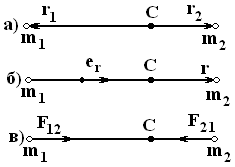 Задачей двух тел наз. задача о движении двух взаимодействующих частиц. Система, образованная частицами, предполагается замкнутой. Центр масс замкнутой системы либо покоится, либо движется прямолинейно и равномерно. Будем решать задачу в системе центра масс (в ц-сист.), поместив начало координат в точку С. В этом случае rC=(m1r1+m2r2)/(m1+m2)=0, т. е. m1r1=–m2r2 (1) (р.a). Введем вектор r =r2–r1(2) определяющий, положение второй частицы относительно первой (р.б). Решая совместно (1) и (2), легко найти,что Задачей двух тел наз. задача о движении двух взаимодействующих частиц. Система, образованная частицами, предполагается замкнутой. Центр масс замкнутой системы либо покоится, либо движется прямолинейно и равномерно. Будем решать задачу в системе центра масс (в ц-сист.), поместив начало координат в точку С. В этом случае rC=(m1r1+m2r2)/(m1+m2)=0, т. е. m1r1=–m2r2 (1) (р.a). Введем вектор r =r2–r1(2) определяющий, положение второй частицы относительно первой (р.б). Решая совместно (1) и (2), легко найти,что  (3) F12=—F21=f(r)еr, где f(r)—ф-ция расстояния между частицами,.положительная для сил притяжения (р.в)и отрицательная для сил отталкивания. Напишем уравнения движения частиц: (3) F12=—F21=f(r)еr, где f(r)—ф-ция расстояния между частицами,.положительная для сил притяжения (р.в)и отрицательная для сил отталкивания. Напишем уравнения движения частиц:  Разделим первое уравнение на m1, а второе—на m2 и вычтем затем из второго уравнения первое. В результате получим: Разделим первое уравнение на m1, а второе—на m2 и вычтем затем из второго уравнения первое. В результате получим: 
Согласно (2) левая часть есть  . Таким образом, . Таким образом,  (4) (4)
Ур-ние (4) можно формально рассматривать как ур-ние движения воображаемой частицы в центральном поле сил. Положение частицы относительно центра сил определяется радиусом-вектором r. Согласно (4) воображаемой частице нужно приписать массу μ, определяемую условием  (5). Отсюда (5). Отсюда  (6). Величина (6) наз. приведенной массой частиц. Таким образом, задача двух тел сводится к задаче о движении одной частицы в центральном поле сил. Найдя из (4) r как функцию t, можно определить по формулам (3) r1(t) и r2(t). Векторы r1 и r2 откладываются из центра масс системы С. Поэтому, чтобы можно было воспользоваться формулами (3), радиус-вектор r воображаемой частицы нужно откладывать также из точки С (для реальных частиц вектор (2) проводится от первой частицы ко второй). Из формул (3) и р. видно, что обе частицы движутся относительно центра масс по геометрически подобным траекториям), причем прямая, соединяющая частицы, все время проходит через центр масс. Закони Кеплера - три емпіричні залежності, що описують рух планет навколо Сонця. 1 закон: Всі планети обертаються навколо Сонця еліптичними орбітами, в одному з фокусів яких перебуває Сонце (всі орбіти планет і тіл Сонячної системи мають один спільний фокус, в якому, власне, і розташовано Сонце). Найближча до Сонця точка орбіти називається перигелієм, а найдальша від нього точка — афелієм. 2 закон: Радіус-вектор планети (тіла Сонячної системи) за рівні проміжки часу описує рівновеликі площі. Лінійна швидкість руху планети неоднакова в різних точках її орбіти: що ближча планета до Сонця, то більша її швидкість. Швидкість руху планети у перигелії найбільша, а в афелії — найменша. Другий закон Кеплера кількісно визначає зміну швидкості руху планети орбітою. З погляду класичної механіки, другий закон Кеплера є проявом закону збереження моменту імпульсу. 3 закон: Квадрати зоряних періодів обертання планет відносяться, як куби великих півосей їхніх орбіт. Третій закон пов'язує властивості орбіт різних планет між собою. Якщо періоди обертання двох планет Т1та Т2, а довжини великих півосей їхніх орбіт, відповідно, а1 та а2, то виконується співвідношення: (6). Величина (6) наз. приведенной массой частиц. Таким образом, задача двух тел сводится к задаче о движении одной частицы в центральном поле сил. Найдя из (4) r как функцию t, можно определить по формулам (3) r1(t) и r2(t). Векторы r1 и r2 откладываются из центра масс системы С. Поэтому, чтобы можно было воспользоваться формулами (3), радиус-вектор r воображаемой частицы нужно откладывать также из точки С (для реальных частиц вектор (2) проводится от первой частицы ко второй). Из формул (3) и р. видно, что обе частицы движутся относительно центра масс по геометрически подобным траекториям), причем прямая, соединяющая частицы, все время проходит через центр масс. Закони Кеплера - три емпіричні залежності, що описують рух планет навколо Сонця. 1 закон: Всі планети обертаються навколо Сонця еліптичними орбітами, в одному з фокусів яких перебуває Сонце (всі орбіти планет і тіл Сонячної системи мають один спільний фокус, в якому, власне, і розташовано Сонце). Найближча до Сонця точка орбіти називається перигелієм, а найдальша від нього точка — афелієм. 2 закон: Радіус-вектор планети (тіла Сонячної системи) за рівні проміжки часу описує рівновеликі площі. Лінійна швидкість руху планети неоднакова в різних точках її орбіти: що ближча планета до Сонця, то більша її швидкість. Швидкість руху планети у перигелії найбільша, а в афелії — найменша. Другий закон Кеплера кількісно визначає зміну швидкості руху планети орбітою. З погляду класичної механіки, другий закон Кеплера є проявом закону збереження моменту імпульсу. 3 закон: Квадрати зоряних періодів обертання планет відносяться, як куби великих півосей їхніх орбіт. Третій закон пов'язує властивості орбіт різних планет між собою. Якщо періоди обертання двох планет Т1та Т2, а довжини великих півосей їхніх орбіт, відповідно, а1 та а2, то виконується співвідношення:  . Цей закон Кеплера пов'язує середні відстані планет від Сонця з їхніми зоряними періодами обертання і надає змогу встановити відносні відстані планет від Сонця, інакше кажучи, дає змогу подати великі півосі всіх планетних орбіт в одиницях великої півосі земної орбіти. Велику піввісь земної орбіти взято за астрономічну одиницю відстаней, але її абсолютне значення було визначено пізніше, лише у XVIII столітті. Відношення кубу півосі до квадрата періоду обертання є сталою для всіх планет Сонячної системи і залежить лише від маси Сонця і гравітаційної сталої, як довів пізніше Ньютон: . Цей закон Кеплера пов'язує середні відстані планет від Сонця з їхніми зоряними періодами обертання і надає змогу встановити відносні відстані планет від Сонця, інакше кажучи, дає змогу подати великі півосі всіх планетних орбіт в одиницях великої півосі земної орбіти. Велику піввісь земної орбіти взято за астрономічну одиницю відстаней, але її абсолютне значення було визначено пізніше, лише у XVIII столітті. Відношення кубу півосі до квадрата періоду обертання є сталою для всіх планет Сонячної системи і залежить лише від маси Сонця і гравітаційної сталої, як довів пізніше Ньютон: 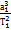 = = 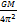 . .
8. Динаміка обертального руху. Обертання твердого тіла навколо нерухомої осі. Момент сили відносно осі. Момент інерції тіла. Момент імпульсу твердого тіла. Основне рівняння динаміки обертального руху. Теорема Штейнера рівняння моментів
Основними кінематичними характеристиками обертального руху тіла в цілому є його кутова швидкість і кутове пришвидшення. Алгебраїчне значення кутової швидкості тіла у даний момент часу дорівнює похідній за часом від кута повороту тіла. Вектор кутової швидкості тіла спрямовується уздовж осі обертання у бік звідки обертання тіла видно проти ходу стрілки годинника. У технічній літературі кутову швидкість часто визначають як чиcло оборотів за хвилину, позначаючи цю величину через n (об/хв) і називається вона частотою обертання. Моментом сили відносно осі називається момент проекції сили на площину, перпендикулярну осі, відносно точки перетину осі з цією площиною. Моментом інерції механічної системи відносно нерухомої осі ("осьовий момент інерції") називається величина Ja, рівна сумі творів мас всіх n матеріальних точок системи на квадрати їх відстаней до осі: Ja= 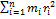 , , 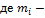 маса i-ї точки, маса i-ї точки, 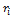 - відстань від i-ї точки до осі. Момент імпульсу твердого тіла відносно осі дорівнює сумі моментів імпульсів окремих частинок: Lz= - відстань від i-ї точки до осі. Момент імпульсу твердого тіла відносно осі дорівнює сумі моментів імпульсів окремих частинок: Lz= 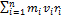 . Основне рівняння динаміки обертального руху твердого тіла: При повороті тіла під дією сили F а нескінченно малий кут d𝛗 точка прикладання сили проходить шлях ds=rd𝛗 і робота дорівнює: dA=Fsinαrd𝛗= M zd𝛗. Оскільки dA=dEk=d( . Основне рівняння динаміки обертального руху твердого тіла: При повороті тіла під дією сили F а нескінченно малий кут d𝛗 точка прикладання сили проходить шлях ds=rd𝛗 і робота дорівнює: dA=Fsinαrd𝛗= M zd𝛗. Оскільки dA=dEk=d(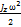 )= )= 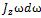 .. Тоді Mzd𝛗= .. Тоді Mzd𝛗= 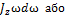 Mz Mz 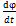 = = 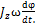 . Звідси рівняння динаміки обертального руху твердого тіла: Mz= . Звідси рівняння динаміки обертального руху твердого тіла: Mz= 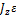 . Теорема Гюйгенса-Штейнера: момент інерції тіла Jz відносно довільної осі дорівнює сумі моменту інерції цього тіла Icm відносно осі, що проходить через центр маси тіла m паралельно до осі, що розглядається і добутку маси тіла на квадрат відстані d між осями: Jz= Jc+md2. Момент інерції досягає свого мінімального значення, коли вісь проходить через центр мас. Наприклад, момент інерції стрижня відносно осі, що проходить через його кінець, становить: J=J0+md2= . Теорема Гюйгенса-Штейнера: момент інерції тіла Jz відносно довільної осі дорівнює сумі моменту інерції цього тіла Icm відносно осі, що проходить через центр маси тіла m паралельно до осі, що розглядається і добутку маси тіла на квадрат відстані d між осями: Jz= Jc+md2. Момент інерції досягає свого мінімального значення, коли вісь проходить через центр мас. Наприклад, момент інерції стрижня відносно осі, що проходить через його кінець, становить: J=J0+md2= 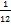 m m 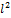 +m( +m(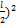 = =  m m 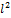 . .
|



 Задачей двух тел наз. задача о движении двух взаимодействующих частиц. Система, образованная частицами, предполагается замкнутой. Центр масс замкнутой системы либо покоится, либо движется прямолинейно и равномерно. Будем решать задачу в системе центра масс (в ц-сист.), поместив начало координат в точку С. В этом случае rC=(m1r1+m2r2)/(m1+m2)=0, т. е. m1r1=–m2r2 (1) (р.a). Введем вектор r =r2–r1(2) определяющий, положение второй частицы относительно первой (р.б). Решая совместно (1) и (2), легко найти,что
Задачей двух тел наз. задача о движении двух взаимодействующих частиц. Система, образованная частицами, предполагается замкнутой. Центр масс замкнутой системы либо покоится, либо движется прямолинейно и равномерно. Будем решать задачу в системе центра масс (в ц-сист.), поместив начало координат в точку С. В этом случае rC=(m1r1+m2r2)/(m1+m2)=0, т. е. m1r1=–m2r2 (1) (р.a). Введем вектор r =r2–r1(2) определяющий, положение второй частицы относительно первой (р.б). Решая совместно (1) и (2), легко найти,что  (3) F12=—F21=f(r)еr, где f(r)—ф-ция расстояния между частицами,.положительная для сил притяжения (р.в)и отрицательная для сил отталкивания. Напишем уравнения движения частиц:
(3) F12=—F21=f(r)еr, где f(r)—ф-ция расстояния между частицами,.положительная для сил притяжения (р.в)и отрицательная для сил отталкивания. Напишем уравнения движения частиц:  Разделим первое уравнение на m1, а второе—на m2 и вычтем затем из второго уравнения первое. В результате получим:
Разделим первое уравнение на m1, а второе—на m2 и вычтем затем из второго уравнения первое. В результате получим: 
 . Таким образом,
. Таким образом,  (4)
(4) (5). Отсюда
(5). Отсюда  (6). Величина (6) наз. приведенной массой частиц. Таким образом, задача двух тел сводится к задаче о движении одной частицы в центральном поле сил. Найдя из (4) r как функцию t, можно определить по формулам (3) r1(t) и r2(t). Векторы r1 и r2 откладываются из центра масс системы С. Поэтому, чтобы можно было воспользоваться формулами (3), радиус-вектор r воображаемой частицы нужно откладывать также из точки С (для реальных частиц вектор (2) проводится от первой частицы ко второй). Из формул (3) и р. видно, что обе частицы движутся относительно центра масс по геометрически подобным траекториям), причем прямая, соединяющая частицы, все время проходит через центр масс. Закони Кеплера - три емпіричні залежності, що описують рух планет навколо Сонця. 1 закон: Всі планети обертаються навколо Сонця еліптичними орбітами, в одному з фокусів яких перебуває Сонце (всі орбіти планет і тіл Сонячної системи мають один спільний фокус, в якому, власне, і розташовано Сонце). Найближча до Сонця точка орбіти називається перигелієм, а найдальша від нього точка — афелієм. 2 закон: Радіус-вектор планети (тіла Сонячної системи) за рівні проміжки часу описує рівновеликі площі. Лінійна швидкість руху планети неоднакова в різних точках її орбіти: що ближча планета до Сонця, то більша її швидкість. Швидкість руху планети у перигелії найбільша, а в афелії — найменша. Другий закон Кеплера кількісно визначає зміну швидкості руху планети орбітою. З погляду класичної механіки, другий закон Кеплера є проявом закону збереження моменту імпульсу. 3 закон: Квадрати зоряних періодів обертання планет відносяться, як куби великих півосей їхніх орбіт. Третій закон пов'язує властивості орбіт різних планет між собою. Якщо періоди обертання двох планет Т1та Т2, а довжини великих півосей їхніх орбіт, відповідно, а1 та а2, то виконується співвідношення:
(6). Величина (6) наз. приведенной массой частиц. Таким образом, задача двух тел сводится к задаче о движении одной частицы в центральном поле сил. Найдя из (4) r как функцию t, можно определить по формулам (3) r1(t) и r2(t). Векторы r1 и r2 откладываются из центра масс системы С. Поэтому, чтобы можно было воспользоваться формулами (3), радиус-вектор r воображаемой частицы нужно откладывать также из точки С (для реальных частиц вектор (2) проводится от первой частицы ко второй). Из формул (3) и р. видно, что обе частицы движутся относительно центра масс по геометрически подобным траекториям), причем прямая, соединяющая частицы, все время проходит через центр масс. Закони Кеплера - три емпіричні залежності, що описують рух планет навколо Сонця. 1 закон: Всі планети обертаються навколо Сонця еліптичними орбітами, в одному з фокусів яких перебуває Сонце (всі орбіти планет і тіл Сонячної системи мають один спільний фокус, в якому, власне, і розташовано Сонце). Найближча до Сонця точка орбіти називається перигелієм, а найдальша від нього точка — афелієм. 2 закон: Радіус-вектор планети (тіла Сонячної системи) за рівні проміжки часу описує рівновеликі площі. Лінійна швидкість руху планети неоднакова в різних точках її орбіти: що ближча планета до Сонця, то більша її швидкість. Швидкість руху планети у перигелії найбільша, а в афелії — найменша. Другий закон Кеплера кількісно визначає зміну швидкості руху планети орбітою. З погляду класичної механіки, другий закон Кеплера є проявом закону збереження моменту імпульсу. 3 закон: Квадрати зоряних періодів обертання планет відносяться, як куби великих півосей їхніх орбіт. Третій закон пов'язує властивості орбіт різних планет між собою. Якщо періоди обертання двох планет Т1та Т2, а довжини великих півосей їхніх орбіт, відповідно, а1 та а2, то виконується співвідношення:  . Цей закон Кеплера пов'язує середні відстані планет від Сонця з їхніми зоряними періодами обертання і надає змогу встановити відносні відстані планет від Сонця, інакше кажучи, дає змогу подати великі півосі всіх планетних орбіт в одиницях великої півосі земної орбіти. Велику піввісь земної орбіти взято за астрономічну одиницю відстаней, але її абсолютне значення було визначено пізніше, лише у XVIII столітті. Відношення кубу півосі до квадрата періоду обертання є сталою для всіх планет Сонячної системи і залежить лише від маси Сонця і гравітаційної сталої, як довів пізніше Ньютон:
. Цей закон Кеплера пов'язує середні відстані планет від Сонця з їхніми зоряними періодами обертання і надає змогу встановити відносні відстані планет від Сонця, інакше кажучи, дає змогу подати великі півосі всіх планетних орбіт в одиницях великої півосі земної орбіти. Велику піввісь земної орбіти взято за астрономічну одиницю відстаней, але її абсолютне значення було визначено пізніше, лише у XVIII столітті. Відношення кубу півосі до квадрата періоду обертання є сталою для всіх планет Сонячної системи і залежить лише від маси Сонця і гравітаційної сталої, як довів пізніше Ньютон: 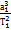 =
= 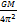 .
.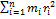 ,
, 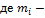 маса i-ї точки,
маса i-ї точки, 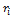 - відстань від i-ї точки до осі. Момент імпульсу твердого тіла відносно осі дорівнює сумі моментів імпульсів окремих частинок: Lz=
- відстань від i-ї точки до осі. Момент імпульсу твердого тіла відносно осі дорівнює сумі моментів імпульсів окремих частинок: Lz= 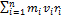 . Основне рівняння динаміки обертального руху твердого тіла: При повороті тіла під дією сили F а нескінченно малий кут d𝛗 точка прикладання сили проходить шлях ds=rd𝛗 і робота дорівнює: dA=Fsinαrd𝛗= M zd𝛗. Оскільки dA=dEk=d(
. Основне рівняння динаміки обертального руху твердого тіла: При повороті тіла під дією сили F а нескінченно малий кут d𝛗 точка прикладання сили проходить шлях ds=rd𝛗 і робота дорівнює: dA=Fsinαrd𝛗= M zd𝛗. Оскільки dA=dEk=d(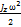 )=
)= 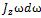 .. Тоді Mzd𝛗=
.. Тоді Mzd𝛗= 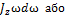 Mz
Mz 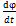 =
= 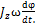 . Звідси рівняння динаміки обертального руху твердого тіла: Mz=
. Звідси рівняння динаміки обертального руху твердого тіла: Mz= 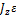 . Теорема Гюйгенса-Штейнера: момент інерції тіла Jz відносно довільної осі дорівнює сумі моменту інерції цього тіла Icm відносно осі, що проходить через центр маси тіла m паралельно до осі, що розглядається і добутку маси тіла на квадрат відстані d між осями: Jz= Jc+md2. Момент інерції досягає свого мінімального значення, коли вісь проходить через центр мас. Наприклад, момент інерції стрижня відносно осі, що проходить через його кінець, становить: J=J0+md2=
. Теорема Гюйгенса-Штейнера: момент інерції тіла Jz відносно довільної осі дорівнює сумі моменту інерції цього тіла Icm відносно осі, що проходить через центр маси тіла m паралельно до осі, що розглядається і добутку маси тіла на квадрат відстані d між осями: Jz= Jc+md2. Момент інерції досягає свого мінімального значення, коли вісь проходить через центр мас. Наприклад, момент інерції стрижня відносно осі, що проходить через його кінець, становить: J=J0+md2= 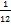 m
m 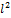 +m(
+m(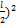 =
=  m
m 


