
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коливання в системі з багатьма ступенями вільності. Нелінійні коливання. Параметричний резонансСодержание книги
Поиск на нашем сайте
У системах з багатьма ступенями вільності на відміну від систем з одним та півтора ступенями вільності, з’являються принципово нові ефекти, пов’язані з обміном енергією між ступенями вільності. Для появи цих ефектів потрібно щонайменше два ступеня вільності. Подальше зростання числа ступенів вільності нічого якісно нового не дає. Тому в цьому розділі розглядатимуться, як правило, саме системи з двома ступенями вільності. Нелінійні коливання - kоливання в фізич. системах, що описуються нелінійними системами звичайних диференціальних рівнянь де містить члени не нижче 2-го ступеня за компонентами вектора - вектор-функція часу - малий параметр (або і). Можливі узагальнення пов'язані з розглядом розривних систем, впливів з розривними характеристиками (напр., типу гістерезису), запізнювання і випадкових впливів, інтегро-диференціальних та диференціально-операторних рівнянь, коливальних систем з розподіленими параметрами, описуваними диференціальними рівняннями з приватними похідними, а також з використанням методів оптимального управління нелінійними коливальними системами. Параметричний резонанс - резонансне збільшення амплітуди коливань гармонічного осцилятора при зміні його параметрів із певною частотою. Усім знайомий приклад параметричного резонансу – гойдалкa.
16. Основні поняття аналітичної механіки (поняття узагальнених сил, імпульсів, координат; канонічні змінні і канонічні перетворення, дужки Пуассона). Величины Если механическая система консервативная, то обобщенная сила равна частной производной от потенциальной энергии по соответствующей обобщенной координате, взятой со знаком минус Обобщенными координатами ( обозначаются В аналітичній механіці поняття імпульсу узагальнюється згідно з означенням Канонічні перетворення - заміна узагальнених координат та узагальнених імпульсів класичної механічної системи на інші, при якій зберігається вигляд основних рівняньгамільтонової механіки - рівнянь Гамільтона. У гамільтоновій механіці стан механічної системи задається узагальненими координатами
Канонічні змінні або змінні дія-кут - пара канонічно спряжених змінних класичної механічної системи, в якій роль імпульсу відіграє змінна дії - адіабатичний інваріант. Твірною функцією для канонічного перетворення до нових змінних є функція
де E - енергія, однозначно зв'язана з адіабатичним інваріантом I. Канонічно спряжена до змінної дії кутова змінна w визначається, як
Рівняння руху в змінних дія-кут мають дуже простий вигляд:
Таким чином, адіабатичний інваріант I є інтегралом руху, а кутова змінна зростає з часом за лінійним законом. За один період кутова змінна збільшується на
Дужками Пуассона в класичній механіці називається вираз
де
17. рівняння лагранжа першого роду. Рівняння Лагранжа другого роду Рівняння Лагранжа другого роду - це диференціальні рівняння руху механічної системи в узагальнених координатах. Як і раніше, вважаємо, що зв'язки, накладені на систему, - голономні, стаціонарні та ідеальні. Для отримання рівнянь руху скористаємося загальним рівнянням динаміки: рівняння лагранжа першого роду. В такому випадку еволюція системи задається наступною системою 3N диференційних рівнянь та s рівнянь зв'язку
Дану систему рівнянь необхідно розв'язувати разом із системою рівнянь для зв'язків. Усього вона має
18. рівняння Гамільтона-Якобі. Рівняння Гамільтона Рівняння Гамільтона (також звані канонічними рівняннями) в фізиці та математики - система диференціальних рівнянь: Рівня́ння Гамільто́на—Я́кобі — рівняння у часткових похідних, яке повністю визначає еволюцію гамільтонової системи класичної механіки. Рівняння має наступне формулювання: Тут
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.85 (0.006 с.) |

 , стоящие при соответствующих вариациях обобщенных координат в формуле для вычисления суммы виртуальных работ активных сил, действующих на точки данной механической системы, называются обобщенными силами.
, стоящие при соответствующих вариациях обобщенных координат в формуле для вычисления суммы виртуальных работ активных сил, действующих на точки данной механической системы, называются обобщенными силами. .
.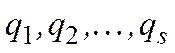 ) называются независимые параметры любой размерности, которые определяют положение механической системы.
) называются независимые параметры любой размерности, которые определяют положение механической системы. ,де
,де  — функція Лагранжа,
— функція Лагранжа,  — узагальнена координата, а
— узагальнена координата, а  — узагальнена швидкість.
— узагальнена швидкість.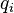 та імпульсами
та імпульсами 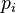 , які вважаються незалежними змінними, та функцією Гамільтона
, які вважаються незалежними змінними, та функцією Гамільтона 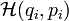 . Рівняння Гамільтона мають вигляд
. Рівняння Гамільтона мають вигляд

 ,
,

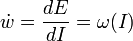
 . Вихідні змінні координата q та імпульса p є періодичними функціями кутової змінної.
. Вихідні змінні координата q та імпульса p є періодичними функціями кутової змінної.
 й
й  — будь які функції узагальнених координат
— будь які функції узагальнених координат  — кількість ступенів свободи системи.
— кількість ступенів свободи системи. -
-  ·
·  )δ
)δ  =0. Для системи із стаціонарними зв'язками віртуальне переміщення k-ї точки виражається, як було показано раніше, через узагальнені координати співвідношенням δ
=0. Для системи із стаціонарними зв'язками віртуальне переміщення k-ї точки виражається, як було показано раніше, через узагальнені координати співвідношенням δ  .
. ,де
,де  — s невизначених множників Лагранжа.
— s невизначених множників Лагранжа. невідомих:
невідомих:  та
та 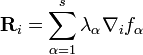 .
. =-
=- 
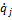 =
= 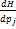 , де точкою над p і q позначена похідна по часу. Система складається з 2 N диференціальних рівнянь першого порядку (j = 1, 2,..., N) для динамічної системи, описуваної N (узагальненими) координатами, які є рівняннями руху (однією з форм таких рівнянь, нарівні з рівняннями Лагранжа, яка є узагальненням ньютонівських рівнянь руху) системи, де H=H(q,p,t)=H(q1,q2,…qn,p1,p2,…pn,t)- так звана функція Гамільтона, також іноді іменована гамільтоніаном, t - Час, qi- (Узагальнені) координати (q1,q2,….qn) i pi- узагальнені імпульси (p1,p2,…pn), що визначають стан системи (точку фазового простору). Рівняння Гамільтона широко використовуються в гамильтоновой механіці та інших галузях теоретичної фізики та математики.
, де точкою над p і q позначена похідна по часу. Система складається з 2 N диференціальних рівнянь першого порядку (j = 1, 2,..., N) для динамічної системи, описуваної N (узагальненими) координатами, які є рівняннями руху (однією з форм таких рівнянь, нарівні з рівняннями Лагранжа, яка є узагальненням ньютонівських рівнянь руху) системи, де H=H(q,p,t)=H(q1,q2,…qn,p1,p2,…pn,t)- так звана функція Гамільтона, також іноді іменована гамільтоніаном, t - Час, qi- (Узагальнені) координати (q1,q2,….qn) i pi- узагальнені імпульси (p1,p2,…pn), що визначають стан системи (точку фазового простору). Рівняння Гамільтона широко використовуються в гамильтоновой механіці та інших галузях теоретичної фізики та математики. .
. — функція Гамільтона для системи із узагальненими координатами
— функція Гамільтона для системи із узагальненими координатами  пробігає значення від одиниці до кількості ступенів свободи гамільтонової системи
пробігає значення від одиниці до кількості ступенів свободи гамільтонової системи  .
.


