

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Механічні коливання. Рух під дією пружних і квазіпружних сил. Рівняння руху найпростіших систем: пружинний, математичний і фізичний маятники. Енергія коливального тіла.
Содержание книги
- Кінематика матеріальної точки. Радіус-вектор, вектори переміщення швидкості і прискорення.
- Обертальний рух матеріальної точки. Кутова швидкість та прискорення. Рух точки по колу. Лінійні й кутові величини, їх зв'язок. Рівняння рівномірного і нерівномірного рухів точки по колу.
- Задача двох тіл. Закони Кеплера.
- Механічні коливання. Рух під дією пружних і квазіпружних сил. Рівняння руху найпростіших систем: пружинний, математичний і фізичний маятники. Енергія коливального тіла.
- Коливання в системі з багатьма ступенями вільності. Нелінійні коливання. Параметричний резонанс
- Рух відносно неінерціальних систем відліку
- І начало термодинаміки. Застосування 1-го начала термодинаміки до ізопроцесів. Поняття про теплоємність. Рівняння Майєра. Адіабатичний процес. Рівняння Пуасона.
- Статистична теорія квантових ідеальних газів. Розподіли Фермі – Дірака та Бозе – Ейнштейна.
- Закон Кулона. Напруженість поля. Принцип суперпозицій. Теорема Гауса та її застосування
- Електричне поле в діелектриках
- Дія магнітного поля на рухомий заряд. Сила лоренца. Визначення питомого заряду електрону. Масспектрометр
- Властивості електромагнітних хвиль.
- Електромагнітні хвилі на межі діелектриків. Електромагнітна природа світла.
- Принцип гюйгенса-френеля. Зони френеля. Прямолінійне поширення світла і дифракція. Дифракція френеля на круглому отворі, круглому екрані, від краю напівобмеженої площини
- Фотоелектричний ефект. Квантова теорія фотоефекту. Фотоелементи та їх застосування. Фотонна теорія світла. Характеристики фотона. Дослідне підтвердження корпускулярної природи світла
- Багатоелектронні атоми. Квантові числа, що описують електрон в атомі. Принцип Паулі. Будова атомної оболонки. Періодична система елементів
- Склад ядра та його характеристики: заряд і масове число ядра, енергія зв'язку, дефект маси. Момент кількості руху і магнітний момент ядра. Експериментальні методи ядерної фізики
- Ядерні сили. Моделі атомних ядер
- Радіоактивність. Види радіоактивності. Закони радіоактивного розпаду. Приклади радіоактивних перетворень ядер. Дозиметрія
- Структурування навчального змісту шкільного курсу фізики.
- Формування знань та умінь з фізики.
- Формування вмінь роботи з навчальною літературою з фізики.
- Використання нових інформаційних технологій навчання.
- Навчальний процес “сутність” і “процес” навчання, “явище” і навчальний процес: урок і система уроків.
- Навчальні конференції та семінари з фізики.
- Введення узагальненого уявлення про фізичну величину на перших уроках фізики в 7 класі.
- V. Розв’язується навчальна проблема.
- Способи організації навчальних занять в історії методики навчання фізики.
- Загальні критерії оцінювання навчальних досягнень учнів у системі загальної середньої освіти.
- Методика навчання фізики. Приклади задач методики фізики-науки. Самостійність науки – методика навчання фізики. Методика навчання, як майстерність вчителя. Зв’язок між наукою і практикою.
Похожие статьи вашей тематики
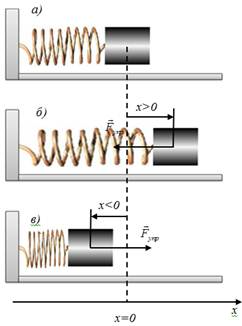 Механі́чні колива́ння — це фізичний процес у механіці, під час якого чергуються інтервали збільшення і зменшення фізичної величини. Бувають прості і складні. Складні коливання- це певним чином скомбіновані прості. Вони найчастіше спостерігаються в живих організмах. Прості коливання в свою чергу поділяються на: а) гармонічні коливання — такі коливання, які відбуваються за законом синуса або косинуса; б ) Реальні (згасаючі) коливання — ті коливання, що мають місце в природі, поступово згасають; в) вимушені коливання — відбуваються при дії на систему зовнішньої сили, яка повинна діяти ритмічно (за законом гармонічних коливань). Розглянемо тіло маси m, закріплене на пружині з коефіцієнтом жорсткості k (масою пружини зневажаємо). Розтягнемо пружину на х. Тоді за законом Гука на тіло буде діяти сила пружності Fпр: 1) величина сили пропорційна величині відхилення системи від положення рівноваги Fупр∼x. 2) напрямок сила протилежний напрямку зсуву, тобто сила завжди спрямована до положення рівноваги (при х > 0, Fпр < 0, при х < 0, Fпр > 0). 3) У положенні рівноваги х = 0 і Fпр = 0. За законом Гука Fпр=- kx. Механі́чні колива́ння — це фізичний процес у механіці, під час якого чергуються інтервали збільшення і зменшення фізичної величини. Бувають прості і складні. Складні коливання- це певним чином скомбіновані прості. Вони найчастіше спостерігаються в живих організмах. Прості коливання в свою чергу поділяються на: а) гармонічні коливання — такі коливання, які відбуваються за законом синуса або косинуса; б ) Реальні (згасаючі) коливання — ті коливання, що мають місце в природі, поступово згасають; в) вимушені коливання — відбуваються при дії на систему зовнішньої сили, яка повинна діяти ритмічно (за законом гармонічних коливань). Розглянемо тіло маси m, закріплене на пружині з коефіцієнтом жорсткості k (масою пружини зневажаємо). Розтягнемо пружину на х. Тоді за законом Гука на тіло буде діяти сила пружності Fпр: 1) величина сили пропорційна величині відхилення системи від положення рівноваги Fупр∼x. 2) напрямок сила протилежний напрямку зсуву, тобто сила завжди спрямована до положення рівноваги (при х > 0, Fпр < 0, при х < 0, Fпр > 0). 3) У положенні рівноваги х = 0 і Fпр = 0. За законом Гука Fпр=- kx.
Систему, що складається з матеріальної точки маси m і абсолютно пружної пружини з коефіцієнтом жорсткості k, у якій можливі вільні коливання, називають пружинним маятником. Запишемо другий закон Ньютона для рис. б): Fупр=ma, Fупр=- kx,
ma=-kx. a=-A 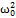 cos( cos(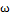 0t+𝛗0)= - 0t+𝛗0)= - 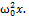 -m -m 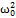 x=-kx ⟹ x=-kx ⟹ 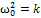 , , 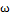 0= 0=  . V= . V= 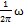 0= 0= 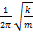 . T= . T=  = = 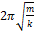 . Якщо сила не є по своїй природі пружної, але підкоряється закону F = -kх, то вона називається квазіпружною силою. Одержимо рівняння пружинного маятника. Урахуємо в записі другого закону Ньютона, що a= . Якщо сила не є по своїй природі пружної, але підкоряється закону F = -kх, то вона називається квазіпружною силою. Одержимо рівняння пружинного маятника. Урахуємо в записі другого закону Ньютона, що a= 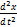 . ma=-kx. m . ma=-kx. m 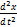 +kx=0 +kx=0 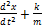 x=0 x=0 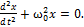 - диференціальне рівняння точки, що робить коливальний рух (диференціальне рівняння пружинного маятника). Розв'язок диференціального рівняння: x=Acos( - диференціальне рівняння точки, що робить коливальний рух (диференціальне рівняння пружинного маятника). Розв'язок диференціального рівняння: x=Acos(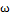 0t+ 𝛗0) - рівняння коливної точки (рівняння коливної пружини). 0t+ 𝛗0) - рівняння коливної точки (рівняння коливної пружини).
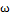 0= 0=  - власна частота коливань. Фізи́чний ма́ятник — тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі, що не проходить через центр маси тіла. - власна частота коливань. Фізи́чний ма́ятник — тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі, що не проходить через центр маси тіла.
Період коливань фізичного маятника визначається формулою: T= 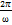 = = 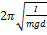 , де I - момент інерції, m - маса, d - віддаль від центра маси тіла до осі, g - прискорення вільного падіння. Зведена довжина фізичного маятника - довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника. Вона дорівнює lr= , де I - момент інерції, m - маса, d - віддаль від центра маси тіла до осі, g - прискорення вільного падіння. Зведена довжина фізичного маятника - довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника. Вона дорівнює lr= 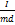 . Математи́чний ма́ятник — теоретична модель маятника, в якій матеріальна точка масою m підвішена на невагомому нерозтяжному стержні довжини l і здійснює рух в вертикальній площині під впливом сил тяжіння з прискоренням вільного падіння g. Модель нехтує розмірами тіла, деформацією підвісу та тертям в точці підвісу стержня. В загальному випадку, якщо відхилити маятник від положення рівноваги та штовхнути його вбік, рух маятника буде складатися з коливань в вертикальних площинах та руху в горизонтальних. При малому відхилені математичний маятник здійснює гармонічні коливання. Якщо відхилення велике, то коливання маятника періодичні, але не гармонічні. Потенціальна енергія математичного маятника дорівнює U=mgh=mgl(1-cos𝛗). Pозрізняють кінетичну та потенціальну енергії тіл. Кінетична енергія визначається масою тіл та швидкістю їх руху: Ek= . Математи́чний ма́ятник — теоретична модель маятника, в якій матеріальна точка масою m підвішена на невагомому нерозтяжному стержні довжини l і здійснює рух в вертикальній площині під впливом сил тяжіння з прискоренням вільного падіння g. Модель нехтує розмірами тіла, деформацією підвісу та тертям в точці підвісу стержня. В загальному випадку, якщо відхилити маятник від положення рівноваги та штовхнути його вбік, рух маятника буде складатися з коливань в вертикальних площинах та руху в горизонтальних. При малому відхилені математичний маятник здійснює гармонічні коливання. Якщо відхилення велике, то коливання маятника періодичні, але не гармонічні. Потенціальна енергія математичного маятника дорівнює U=mgh=mgl(1-cos𝛗). Pозрізняють кінетичну та потенціальну енергії тіл. Кінетична енергія визначається масою тіл та швидкістю їх руху: Ek= 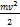 . Потенціальну енергію тіла у полі сил тяжіння визначають за формулою Еп = mgh, а потенціальну енергію пружно деформованого тіла (наприклад, пружини) Eп= . Потенціальну енергію тіла у полі сил тяжіння визначають за формулою Еп = mgh, а потенціальну енергію пружно деформованого тіла (наприклад, пружини) Eп= 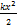 . .
12. Затухаючі коливання. Коефіцієнт затухання, логарифмічний. декремент, добротність
Затухаючі коливання - коливання, енергія яких зменшується з часом. Нескінченно що триває процес виду u(t)=Acos(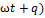 в природі неможливий. Вільні коливання будь-якого осцилятора рано чи пізно загасають і припиняються. Тому на практиці звичайно мають справу з затухаючими коливаннями. Вони характеризуються тим, що амплітуда коливань A є спадною функцією. Зазвичай загасання відбувається під дією сил опору середовища, найбільш часто висловлюються лінійною залежністю від швидкості коливань або її квадрата. В акустиці: загасання - зменшення рівня сигналу до повної нечутності. Kоефіцієнт затухання - це величина, обернена до проміжку часу, за який амплітуда коливання зменшується в е=2,71.. разів. Швидкість затухання коливання характеризується декрементом затухання д. Декремент затухання - це відношення двох амплітуд, розділених проміжком часу, що дорівнює одному періоду Т. Логарифмічний декремент затухання є величина, обернена до числа періодів, за які амплітуда зменшується в е разів. Добротність – характеристика резонансних властивостей системи. Відношення амплітуди коливань системи при резонансі до амплітуди коливань далеко від нього для вимушених коливань, або відношення енергії запасеної в системі до втрат енергії за одне коливання, для вільних коливань. На практиці найчастіше вимірюють добротність котушок індуктивності, конденсаторів, коливальних контурів тощо. в природі неможливий. Вільні коливання будь-якого осцилятора рано чи пізно загасають і припиняються. Тому на практиці звичайно мають справу з затухаючими коливаннями. Вони характеризуються тим, що амплітуда коливань A є спадною функцією. Зазвичай загасання відбувається під дією сил опору середовища, найбільш часто висловлюються лінійною залежністю від швидкості коливань або її квадрата. В акустиці: загасання - зменшення рівня сигналу до повної нечутності. Kоефіцієнт затухання - це величина, обернена до проміжку часу, за який амплітуда коливання зменшується в е=2,71.. разів. Швидкість затухання коливання характеризується декрементом затухання д. Декремент затухання - це відношення двох амплітуд, розділених проміжком часу, що дорівнює одному періоду Т. Логарифмічний декремент затухання є величина, обернена до числа періодів, за які амплітуда зменшується в е разів. Добротність – характеристика резонансних властивостей системи. Відношення амплітуди коливань системи при резонансі до амплітуди коливань далеко від нього для вимушених коливань, або відношення енергії запасеної в системі до втрат енергії за одне коливання, для вільних коливань. На практиці найчастіше вимірюють добротність котушок індуктивності, конденсаторів, коливальних контурів тощо.
13. Вимушені коливання. Диференціальне рівняння вимушених коливань та аналіз його розв'язку. Резонанс
Вимушеними коливання - відбуваються під дією періодичної зовнішньої сили. Щоб у реальній коливальній системі отримати незатухаючі коливання, треба компенсувати втрати енергії. Така компенсація можлива за допомогою якого-небудь періодичного чинника, який змінюється за гармонійним законом: x(t)=x0cos 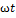 . Для вимушених коливань характерне явище резонансу — значне збільшення амплітуди коливань тоді, коли частота збурення збігається із одною з власних частот коливної системи. Фізична величина У, яка здійснює гармонічні коливання, задовільняє диференціальне рівняння . Для вимушених коливань характерне явище резонансу — значне збільшення амплітуди коливань тоді, коли частота збурення збігається із одною з власних частот коливної системи. Фізична величина У, яка здійснює гармонічні коливання, задовільняє диференціальне рівняння  + + 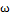 2y=0. У цьому випадку амплітуда коливань визначається початковими умовами. Гармонічний осцилятор із частотою 2y=0. У цьому випадку амплітуда коливань визначається початковими умовами. Гармонічний осцилятор із частотою 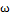 0 може здійснювати гармонічні коливання на іншій частоті 0 може здійснювати гармонічні коливання на іншій частоті 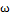 під впливом зовнішньої дії з цією частотою. У такому випадку гармонічні коливання величини y задовольняє диференціальному рівнянню під впливом зовнішньої дії з цією частотою. У такому випадку гармонічні коливання величини y задовольняє диференціальному рівнянню  + + 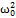 y=f cos( y=f cos(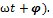 Такі коливання називаються вимушеними. Амплітуда вимушених коливань визначається величиною зовнішньої дії. Резона́нс — явище сильного зростання амплітуди вимушеного коливання у разі, коли частота зовнішньої сили збігається з власною частотою коливань. Резонанс характеризують інтенсивністю, напівшириною спектральної лінії та добротністю. Здебільшого резонанс наближено описують кривою Лоренца: I Такі коливання називаються вимушеними. Амплітуда вимушених коливань визначається величиною зовнішньої дії. Резона́нс — явище сильного зростання амплітуди вимушеного коливання у разі, коли частота зовнішньої сили збігається з власною частотою коливань. Резонанс характеризують інтенсивністю, напівшириною спектральної лінії та добротністю. Здебільшого резонанс наближено описують кривою Лоренца: I 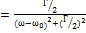 де ω — частота зовнішньої сили, ω0 — частота власного коливання, Γ — стала затухання, яку називають також шириною лінії. Часто приводиться також γ= Γ/2 — півширина лінії. де ω — частота зовнішньої сили, ω0 — частота власного коливання, Γ — стала затухання, яку називають також шириною лінії. Часто приводиться також γ= Γ/2 — півширина лінії.
14. Хвилі. Рівняння біжучої хвилі. Повздовжні та поперечні хвилі. Інтерференція хвиль. Стоячі хвилі
Xвиля — процес розповсюдження коливань у будь-якому середовищі чи вакуумі. Хвильовий процес — процес передачі коливань. Розглянемо хвилю, що біжить в додатному напрямку осi: 0x: 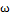 1=a1cos(kx- 1=a1cos(kx- 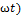 . Відстань між двома точками,які знаходяться в однаковій фазі збурення (наприклад, між послідовними максимумами чи мінімумами)називають довжиною хвилі. k 𝛌=2π. Хвильовий процес пов'язаний з переносом енергії. Для гармонічної хвилі . Відстань між двома точками,які знаходяться в однаковій фазі збурення (наприклад, між послідовними максимумами чи мінімумами)називають довжиною хвилі. k 𝛌=2π. Хвильовий процес пов'язаний з переносом енергії. Для гармонічної хвилі 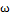 1(x,t), що біжить в додатному напрямку осі 0x для потоку енергії маємо вираз E= 1(x,t), що біжить в додатному напрямку осі 0x для потоку енергії маємо вираз E=  Tk Tk 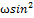 (kx- (kx- 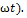 Для фіксованої точки струни цей потік змінюється в часі, але завжди більший або дорівнює нулю. Поперечна хвиля - хвиля, в якій коливання відбуваються в площині, перпендикулярній до напрямку поширення. До поперечних хвиль належать електромагнітні хвилі у вакуумі. Повздовжня хвиля - хвиля, в якій коливання в кожній точці простору паралельні напрямку розповсюдження. В повздовжній електромагнітній хвилі вектор напруженості електричного поля направлений паралельно напрямку розповсюдження. Прикладом повздовжніх хвиль є звукові хвилі в газі. Інтерфере́нція хвиль — явище накладання двох або більше когерентних світлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум). Інтерференція спостерігається у когерентних хвиль довільної природи — поверхневих (на воді), поперечних та повздовжніх звукових, електромагнітних (світло, радіохвилі), хвиль де Бройля. При інтерференції результуюче коливання є геометричною сумою коливань обох хвиль у відповідних точках. Цей принцип суперпозиції як правило є точним і порушується у окремих випадках, в деяких середовищах, коли амплітуда коливань є дуже високою (нелінійна оптика, нелінійна акустика). Найпростішим випадком інтерференції є накладання двох гармонічних хвиль з однаковою частотою і поляризацією. В такому випадку результуюча амплітуда А вираховується за формулою: A= Для фіксованої точки струни цей потік змінюється в часі, але завжди більший або дорівнює нулю. Поперечна хвиля - хвиля, в якій коливання відбуваються в площині, перпендикулярній до напрямку поширення. До поперечних хвиль належать електромагнітні хвилі у вакуумі. Повздовжня хвиля - хвиля, в якій коливання в кожній точці простору паралельні напрямку розповсюдження. В повздовжній електромагнітній хвилі вектор напруженості електричного поля направлений паралельно напрямку розповсюдження. Прикладом повздовжніх хвиль є звукові хвилі в газі. Інтерфере́нція хвиль — явище накладання двох або більше когерентних світлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум). Інтерференція спостерігається у когерентних хвиль довільної природи — поверхневих (на воді), поперечних та повздовжніх звукових, електромагнітних (світло, радіохвилі), хвиль де Бройля. При інтерференції результуюче коливання є геометричною сумою коливань обох хвиль у відповідних точках. Цей принцип суперпозиції як правило є точним і порушується у окремих випадках, в деяких середовищах, коли амплітуда коливань є дуже високою (нелінійна оптика, нелінійна акустика). Найпростішим випадком інтерференції є накладання двох гармонічних хвиль з однаковою частотою і поляризацією. В такому випадку результуюча амплітуда А вираховується за формулою: A= 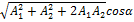 , де , де  та та 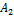 — амплітуди відповідних хвиль, — амплітуди відповідних хвиль,  — різниця фаз цих хвиль. Явище інтерференції використовується, наприклад, в радіотехніці і акустиці для створення складних антен. Стоя́ча (стійна) хви́ля — така хвиля, в якій будь-яка фаза коливань не поширюється в просторі. Вона утворюється в результаті накладання двох біжних (рухомих) хвиль, які поширюються назустріч одна одній і мають деякий зсув фаз. У біжній хвилі відбувається перенесення енергії, а в х. с. через площини, в яких розташовані вузли, енергія не перетікаєУ випадку гармонічних коливань в одновимірному середовищі стояча хвиля описується формулою:u=u0cosk·x·cos( — різниця фаз цих хвиль. Явище інтерференції використовується, наприклад, в радіотехніці і акустиці для створення складних антен. Стоя́ча (стійна) хви́ля — така хвиля, в якій будь-яка фаза коливань не поширюється в просторі. Вона утворюється в результаті накладання двох біжних (рухомих) хвиль, які поширюються назустріч одна одній і мають деякий зсув фаз. У біжній хвилі відбувається перенесення енергії, а в х. с. через площини, в яких розташовані вузли, енергія не перетікаєУ випадку гармонічних коливань в одновимірному середовищі стояча хвиля описується формулою:u=u0cosk·x·cos(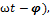 де u — збурення в точці х в момент часу t, u0— амплітуда стоячої хвилі, де u — збурення в точці х в момент часу t, u0— амплітуда стоячої хвилі, 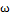 — частота, k — хвильовий вектор, 𝛗— фаза. При існуванні в середовищі стоячої хвилі, існують точки, амплітуда коливань у яких дорівнює нулю. Ці точки називаються вузлами стоячої хвилі. Точки, в яких коливання мають максимальну амплітуду називаються пучностями. Стоячі хвилі є розв'язками тих же хвильових рівнянь. Їх можна уявити собі, як суперпозицію хвиль, що розповсюджуються в протилежних напрямках. — частота, k — хвильовий вектор, 𝛗— фаза. При існуванні в середовищі стоячої хвилі, існують точки, амплітуда коливань у яких дорівнює нулю. Ці точки називаються вузлами стоячої хвилі. Точки, в яких коливання мають максимальну амплітуду називаються пучностями. Стоячі хвилі є розв'язками тих же хвильових рівнянь. Їх можна уявити собі, як суперпозицію хвиль, що розповсюджуються в протилежних напрямках.
|



 Механі́чні колива́ння — це фізичний процес у механіці, під час якого чергуються інтервали збільшення і зменшення фізичної величини. Бувають прості і складні. Складні коливання- це певним чином скомбіновані прості. Вони найчастіше спостерігаються в живих організмах. Прості коливання в свою чергу поділяються на: а) гармонічні коливання — такі коливання, які відбуваються за законом синуса або косинуса; б ) Реальні (згасаючі) коливання — ті коливання, що мають місце в природі, поступово згасають; в) вимушені коливання — відбуваються при дії на систему зовнішньої сили, яка повинна діяти ритмічно (за законом гармонічних коливань). Розглянемо тіло маси m, закріплене на пружині з коефіцієнтом жорсткості k (масою пружини зневажаємо). Розтягнемо пружину на х. Тоді за законом Гука на тіло буде діяти сила пружності Fпр: 1) величина сили пропорційна величині відхилення системи від положення рівноваги Fупр∼x. 2) напрямок сила протилежний напрямку зсуву, тобто сила завжди спрямована до положення рівноваги (при х > 0, Fпр < 0, при х < 0, Fпр > 0). 3) У положенні рівноваги х = 0 і Fпр = 0. За законом Гука Fпр=- kx.
Механі́чні колива́ння — це фізичний процес у механіці, під час якого чергуються інтервали збільшення і зменшення фізичної величини. Бувають прості і складні. Складні коливання- це певним чином скомбіновані прості. Вони найчастіше спостерігаються в живих організмах. Прості коливання в свою чергу поділяються на: а) гармонічні коливання — такі коливання, які відбуваються за законом синуса або косинуса; б ) Реальні (згасаючі) коливання — ті коливання, що мають місце в природі, поступово згасають; в) вимушені коливання — відбуваються при дії на систему зовнішньої сили, яка повинна діяти ритмічно (за законом гармонічних коливань). Розглянемо тіло маси m, закріплене на пружині з коефіцієнтом жорсткості k (масою пружини зневажаємо). Розтягнемо пружину на х. Тоді за законом Гука на тіло буде діяти сила пружності Fпр: 1) величина сили пропорційна величині відхилення системи від положення рівноваги Fупр∼x. 2) напрямок сила протилежний напрямку зсуву, тобто сила завжди спрямована до положення рівноваги (при х > 0, Fпр < 0, при х < 0, Fпр > 0). 3) У положенні рівноваги х = 0 і Fпр = 0. За законом Гука Fпр=- kx.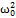 cos(
cos(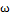 0t+𝛗0)= -
0t+𝛗0)= - 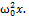 -m
-m 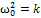 ,
,  . V=
. V= 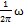 0=
0= 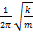 . T=
. T=  =
= 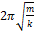 . Якщо сила не є по своїй природі пружної, але підкоряється закону F = -kх, то вона називається квазіпружною силою. Одержимо рівняння пружинного маятника. Урахуємо в записі другого закону Ньютона, що a=
. Якщо сила не є по своїй природі пружної, але підкоряється закону F = -kх, то вона називається квазіпружною силою. Одержимо рівняння пружинного маятника. Урахуємо в записі другого закону Ньютона, що a= 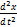 . ma=-kx. m
. ma=-kx. m 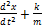 x=0
x=0 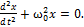 - диференціальне рівняння точки, що робить коливальний рух (диференціальне рівняння пружинного маятника). Розв'язок диференціального рівняння: x=Acos(
- диференціальне рівняння точки, що робить коливальний рух (диференціальне рівняння пружинного маятника). Розв'язок диференціального рівняння: x=Acos(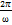 =
= 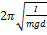 , де I - момент інерції, m - маса, d - віддаль від центра маси тіла до осі, g - прискорення вільного падіння. Зведена довжина фізичного маятника - довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника. Вона дорівнює lr=
, де I - момент інерції, m - маса, d - віддаль від центра маси тіла до осі, g - прискорення вільного падіння. Зведена довжина фізичного маятника - довжина такого математичного маятника, період коливань якого збігається з періодом коливань даного фізичного маятника. Вона дорівнює lr= 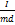 . Математи́чний ма́ятник — теоретична модель маятника, в якій матеріальна точка масою m підвішена на невагомому нерозтяжному стержні довжини l і здійснює рух в вертикальній площині під впливом сил тяжіння з прискоренням вільного падіння g. Модель нехтує розмірами тіла, деформацією підвісу та тертям в точці підвісу стержня. В загальному випадку, якщо відхилити маятник від положення рівноваги та штовхнути його вбік, рух маятника буде складатися з коливань в вертикальних площинах та руху в горизонтальних. При малому відхилені математичний маятник здійснює гармонічні коливання. Якщо відхилення велике, то коливання маятника періодичні, але не гармонічні. Потенціальна енергія математичного маятника дорівнює U=mgh=mgl(1-cos𝛗). Pозрізняють кінетичну та потенціальну енергії тіл. Кінетична енергія визначається масою тіл та швидкістю їх руху: Ek=
. Математи́чний ма́ятник — теоретична модель маятника, в якій матеріальна точка масою m підвішена на невагомому нерозтяжному стержні довжини l і здійснює рух в вертикальній площині під впливом сил тяжіння з прискоренням вільного падіння g. Модель нехтує розмірами тіла, деформацією підвісу та тертям в точці підвісу стержня. В загальному випадку, якщо відхилити маятник від положення рівноваги та штовхнути його вбік, рух маятника буде складатися з коливань в вертикальних площинах та руху в горизонтальних. При малому відхилені математичний маятник здійснює гармонічні коливання. Якщо відхилення велике, то коливання маятника періодичні, але не гармонічні. Потенціальна енергія математичного маятника дорівнює U=mgh=mgl(1-cos𝛗). Pозрізняють кінетичну та потенціальну енергії тіл. Кінетична енергія визначається масою тіл та швидкістю їх руху: Ek= 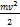 . Потенціальну енергію тіла у полі сил тяжіння визначають за формулою Еп = mgh, а потенціальну енергію пружно деформованого тіла (наприклад, пружини) Eп=
. Потенціальну енергію тіла у полі сил тяжіння визначають за формулою Еп = mgh, а потенціальну енергію пружно деформованого тіла (наприклад, пружини) Eп= 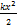 .
.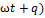 в природі неможливий. Вільні коливання будь-якого осцилятора рано чи пізно загасають і припиняються. Тому на практиці звичайно мають справу з затухаючими коливаннями. Вони характеризуються тим, що амплітуда коливань A є спадною функцією. Зазвичай загасання відбувається під дією сил опору середовища, найбільш часто висловлюються лінійною залежністю від швидкості коливань або її квадрата. В акустиці: загасання - зменшення рівня сигналу до повної нечутності. Kоефіцієнт затухання - це величина, обернена до проміжку часу, за який амплітуда коливання зменшується в е=2,71.. разів. Швидкість затухання коливання характеризується декрементом затухання д. Декремент затухання - це відношення двох амплітуд, розділених проміжком часу, що дорівнює одному періоду Т. Логарифмічний декремент затухання є величина, обернена до числа періодів, за які амплітуда зменшується в е разів. Добротність – характеристика резонансних властивостей системи. Відношення амплітуди коливань системи при резонансі до амплітуди коливань далеко від нього для вимушених коливань, або відношення енергії запасеної в системі до втрат енергії за одне коливання, для вільних коливань. На практиці найчастіше вимірюють добротність котушок індуктивності, конденсаторів, коливальних контурів тощо.
в природі неможливий. Вільні коливання будь-якого осцилятора рано чи пізно загасають і припиняються. Тому на практиці звичайно мають справу з затухаючими коливаннями. Вони характеризуються тим, що амплітуда коливань A є спадною функцією. Зазвичай загасання відбувається під дією сил опору середовища, найбільш часто висловлюються лінійною залежністю від швидкості коливань або її квадрата. В акустиці: загасання - зменшення рівня сигналу до повної нечутності. Kоефіцієнт затухання - це величина, обернена до проміжку часу, за який амплітуда коливання зменшується в е=2,71.. разів. Швидкість затухання коливання характеризується декрементом затухання д. Декремент затухання - це відношення двох амплітуд, розділених проміжком часу, що дорівнює одному періоду Т. Логарифмічний декремент затухання є величина, обернена до числа періодів, за які амплітуда зменшується в е разів. Добротність – характеристика резонансних властивостей системи. Відношення амплітуди коливань системи при резонансі до амплітуди коливань далеко від нього для вимушених коливань, або відношення енергії запасеної в системі до втрат енергії за одне коливання, для вільних коливань. На практиці найчастіше вимірюють добротність котушок індуктивності, конденсаторів, коливальних контурів тощо.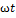 . Для вимушених коливань характерне явище резонансу — значне збільшення амплітуди коливань тоді, коли частота збурення збігається із одною з власних частот коливної системи. Фізична величина У, яка здійснює гармонічні коливання, задовільняє диференціальне рівняння
. Для вимушених коливань характерне явище резонансу — значне збільшення амплітуди коливань тоді, коли частота збурення збігається із одною з власних частот коливної системи. Фізична величина У, яка здійснює гармонічні коливання, задовільняє диференціальне рівняння  +
+ 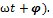 Такі коливання називаються вимушеними. Амплітуда вимушених коливань визначається величиною зовнішньої дії. Резона́нс — явище сильного зростання амплітуди вимушеного коливання у разі, коли частота зовнішньої сили збігається з власною частотою коливань. Резонанс характеризують інтенсивністю, напівшириною спектральної лінії та добротністю. Здебільшого резонанс наближено описують кривою Лоренца: I
Такі коливання називаються вимушеними. Амплітуда вимушених коливань визначається величиною зовнішньої дії. Резона́нс — явище сильного зростання амплітуди вимушеного коливання у разі, коли частота зовнішньої сили збігається з власною частотою коливань. Резонанс характеризують інтенсивністю, напівшириною спектральної лінії та добротністю. Здебільшого резонанс наближено описують кривою Лоренца: I 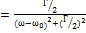 де ω — частота зовнішньої сили, ω0 — частота власного коливання, Γ — стала затухання, яку називають також шириною лінії. Часто приводиться також γ= Γ/2 — півширина лінії.
де ω — частота зовнішньої сили, ω0 — частота власного коливання, Γ — стала затухання, яку називають також шириною лінії. Часто приводиться також γ= Γ/2 — півширина лінії.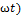 . Відстань між двома точками,які знаходяться в однаковій фазі збурення (наприклад, між послідовними максимумами чи мінімумами)називають довжиною хвилі. k 𝛌=2π. Хвильовий процес пов'язаний з переносом енергії. Для гармонічної хвилі
. Відстань між двома точками,які знаходяться в однаковій фазі збурення (наприклад, між послідовними максимумами чи мінімумами)називають довжиною хвилі. k 𝛌=2π. Хвильовий процес пов'язаний з переносом енергії. Для гармонічної хвилі  Tk
Tk 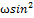 (kx-
(kx- 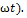 Для фіксованої точки струни цей потік змінюється в часі, але завжди більший або дорівнює нулю. Поперечна хвиля - хвиля, в якій коливання відбуваються в площині, перпендикулярній до напрямку поширення. До поперечних хвиль належать електромагнітні хвилі у вакуумі. Повздовжня хвиля - хвиля, в якій коливання в кожній точці простору паралельні напрямку розповсюдження. В повздовжній електромагнітній хвилі вектор напруженості електричного поля направлений паралельно напрямку розповсюдження. Прикладом повздовжніх хвиль є звукові хвилі в газі. Інтерфере́нція хвиль — явище накладання двох або більше когерентних світлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум). Інтерференція спостерігається у когерентних хвиль довільної природи — поверхневих (на воді), поперечних та повздовжніх звукових, електромагнітних (світло, радіохвилі), хвиль де Бройля. При інтерференції результуюче коливання є геометричною сумою коливань обох хвиль у відповідних точках. Цей принцип суперпозиції як правило є точним і порушується у окремих випадках, в деяких середовищах, коли амплітуда коливань є дуже високою (нелінійна оптика, нелінійна акустика). Найпростішим випадком інтерференції є накладання двох гармонічних хвиль з однаковою частотою і поляризацією. В такому випадку результуюча амплітуда А вираховується за формулою: A=
Для фіксованої точки струни цей потік змінюється в часі, але завжди більший або дорівнює нулю. Поперечна хвиля - хвиля, в якій коливання відбуваються в площині, перпендикулярній до напрямку поширення. До поперечних хвиль належать електромагнітні хвилі у вакуумі. Повздовжня хвиля - хвиля, в якій коливання в кожній точці простору паралельні напрямку розповсюдження. В повздовжній електромагнітній хвилі вектор напруженості електричного поля направлений паралельно напрямку розповсюдження. Прикладом повздовжніх хвиль є звукові хвилі в газі. Інтерфере́нція хвиль — явище накладання двох або більше когерентних світлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум). Інтерференція спостерігається у когерентних хвиль довільної природи — поверхневих (на воді), поперечних та повздовжніх звукових, електромагнітних (світло, радіохвилі), хвиль де Бройля. При інтерференції результуюче коливання є геометричною сумою коливань обох хвиль у відповідних точках. Цей принцип суперпозиції як правило є точним і порушується у окремих випадках, в деяких середовищах, коли амплітуда коливань є дуже високою (нелінійна оптика, нелінійна акустика). Найпростішим випадком інтерференції є накладання двох гармонічних хвиль з однаковою частотою і поляризацією. В такому випадку результуюча амплітуда А вираховується за формулою: A= 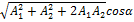 , де
, де  та
та 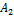 — амплітуди відповідних хвиль,
— амплітуди відповідних хвиль,  — різниця фаз цих хвиль. Явище інтерференції використовується, наприклад, в радіотехніці і акустиці для створення складних антен. Стоя́ча (стійна) хви́ля — така хвиля, в якій будь-яка фаза коливань не поширюється в просторі. Вона утворюється в результаті накладання двох біжних (рухомих) хвиль, які поширюються назустріч одна одній і мають деякий зсув фаз. У біжній хвилі відбувається перенесення енергії, а в х. с. через площини, в яких розташовані вузли, енергія не перетікаєУ випадку гармонічних коливань в одновимірному середовищі стояча хвиля описується формулою:u=u0cosk·x·cos(
— різниця фаз цих хвиль. Явище інтерференції використовується, наприклад, в радіотехніці і акустиці для створення складних антен. Стоя́ча (стійна) хви́ля — така хвиля, в якій будь-яка фаза коливань не поширюється в просторі. Вона утворюється в результаті накладання двох біжних (рухомих) хвиль, які поширюються назустріч одна одній і мають деякий зсув фаз. У біжній хвилі відбувається перенесення енергії, а в х. с. через площини, в яких розташовані вузли, енергія не перетікаєУ випадку гармонічних коливань в одновимірному середовищі стояча хвиля описується формулою:u=u0cosk·x·cos(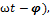 де u — збурення в точці х в момент часу t, u0— амплітуда стоячої хвилі,
де u — збурення в точці х в момент часу t, u0— амплітуда стоячої хвилі, 


