
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дві задачі динаміки вільної матеріальної точкиСодержание книги Поиск на нашем сайте
1. Пряма або перша задача динаміки. Знаючи масу матеріальної точки і її закон руху, знайти силу дії на цю точку чи рівнодійну сил, що спричинили цей рух. В залежності від того в якій формі заданий закон руху матеріальної точки для визначення сили можна використовувати рівняння руху в векторній, координатній чи дійсній формі. Наприклад: задані кінематичні рівняння в координатній формі:
тоді
2. Обернена або друга або друга задача динаміки. Визначити закон руху матеріальної точки даної маси m за відомою силою F. Задано початкове положення цієї точки і її початкову швидкість. Загальні теореми динаміки:
26. Теорема про кількості механічної системи в інерційній системі відліку. Нехай механічна система складається з матеріальних точок Тоді запишемо Другий Закон Ньютона:
Приймаються до уваги властивості внутрішніх сил:
де Q – кількісних рух механічної системи в нерухомій системі відліку. Терема: Похідна часу від кількості руху механічної системи вираховується в будь-якій інерційній системі відліку рівна головному вектору всіх дій на систему зовнішніх сил. Проектуючи (4.4) на вісі нерухомої системи координат Аξηζ отримуємо:
Похідна по часу від проекції механічної системи на осі системи координат пов’язані з будь-якої інерційної системи відліку рівна відповідним проекціям на ті ж осі головного вектора всіх діючих на систему зовнішніх сил. Припустимо, що головний вектор всіх зовнішніх сил діючи на механічну систему може бути виражений функцією часу
де
Такий імпульс сили
Проектуючи на осі нерухомої системи координат Аξηζ отримуємо:
Модуль та напрямок головного імпульсу визначаються:
Підставляючи (4.7), (4.6) отримуємо
27. Теорема про рух центра мас в механічній системі. Тоді рівняння 2 закону Ньютона:
В проекції на координати осі x, y, z радіус-вектора центра мас. Або що те ж саме координати центра мас визначаємо за формулами:
Рівність (4.12) виражає другий закон Ньютона для матеріальної точки в центрі мас механічної системи, якщо маса цієї точки рівна сумі мас, що входять в цю систему і до неї прикладена сила, рівна головному вектору усіх зовнішніх сил. Теорема: Центр мас механічної системи рухаються як вільна матеріальна точка, маса якої рівна масі усієї системи і на яку діє сила, рівна головному вектору усіх зовнішніх сил. Проектуючи (4.12) на осі нерухомої системи координат Аξηζ і отримуємо:
В рівнянні (4.13) називається диференційним рівнянням руху центра мас. 1. Закони збереження кількості руху механічної системи. Нехай механічна система є замкнутою, тобто на точки системи не діють зовнішні сили, тоді з формули (4.4) слідує:
де Q – визначається з початкової умови руху. Якщо при
де
де Рівність (4.16) виражає закон збереження швидкості центра мас замкненої механічної системи рухається в інерційній системі відліку. Центр мас такої системи рухається з постійною швидкістю U=0. Закон збереження у вигляді (4.14) чи (4.16) є першим інтегралом в рівнянні руху в векторній формі. З (4.16) враховуючи, що
(4.17) називається другим інтегралом в векторній формі, де
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.126.170 (0.009 с.) |

 (4.1)
(4.1)
 (4.2)
(4.2)
 (4.3)
(4.3)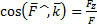
 масою
масою  . Кожна рухається відносно нерухомої системи відліку Аξɳζ Сили діють на точки механічної системи розкладемо на зовнішні і внутрішні, позначаючи через
. Кожна рухається відносно нерухомої системи відліку Аξɳζ Сили діють на точки механічної системи розкладемо на зовнішні і внутрішні, позначаючи через  рівнодійну всіх зовнішніх сил, через
рівнодійну всіх зовнішніх сил, через  рівнодійну всіх внутрішніх сил.
рівнодійну всіх внутрішніх сил.



 (4.4)
(4.4) ;
;  ;
;  (4.5)
(4.5) . Тоді вираз (4.3) можна переписати:
. Тоді вираз (4.3) можна переписати: (4.6)
(4.6) – кількість руху механічної сили в початку відліку.
– кількість руху механічної сили в початку відліку. – кількість руху механічної сили в момент часу t.
– кількість руху механічної сили в момент часу t.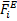 буде рівний (4.7)
буде рівний (4.7) (4.7)
(4.7)
 (4.8)
(4.8)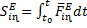
 (4.9)
(4.9) (4.10)
(4.10) (4.11)
(4.11) (4.12)
(4.12)
 – радіус-вектор центра мас.
– радіус-вектор центра мас.
 (4.13)
(4.13)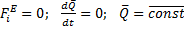 (4.14)
(4.14)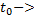 швидкість точок механічної системи рівна
швидкість точок механічної системи рівна  , то наша
, то наша  . І тоді (4.14) приймає вигляд:
. І тоді (4.14) приймає вигляд: (4.15)
(4.15)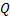 і
і  – компоненти руху механічної системи відповідно кінцевий і початковий моменти часу. Рівність (4.14) чи (4.15) виражають закон збереження комплексів руху замкненої механічної системи і в інерційній системі відліку.
– компоненти руху механічної системи відповідно кінцевий і початковий моменти часу. Рівність (4.14) чи (4.15) виражають закон збереження комплексів руху замкненої механічної системи і в інерційній системі відліку. (4.16)
(4.16) і
і 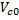 – швидкості центра мас механічної системи відповідно в кінцевому і початковому моментах часу.
– швидкості центра мас механічної системи відповідно в кінцевому і початковому моментах часу.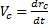 знаходимо
знаходимо 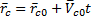 (4.17)
(4.17) – радіус-вектор центра мас в початковий момент часу. (4.17) слідує, що в інерційна система відліку рухається рівномірно і прямолінійно.
– радіус-вектор центра мас в початковий момент часу. (4.17) слідує, що в інерційна система відліку рухається рівномірно і прямолінійно.


