
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поступальний рух твердого тіла. Розподіл лінійних швидкостей і прискорень.Содержание книги
Поиск на нашем сайте
Рух тіла, при якому пряма, що проходить через дві будь-які точки цього тіло, переміщається, залишаючись паралельно в початковому положенню називається поступальним рухом твердого тіла. Властивості поступального руху твердого тіла визначається теоремою: Теорема. При поступальному русі твердого тіла, усі його точки описують (конкурентними) однакові траєкторії й рухається з однаковими швидкостями й прискореннями. Доведення. Розглянь поступальний рух тіла G щодо нерухливої системі координат Aξɳζ.
Виберемо довільну точку О цього тіла як початку рухливої системі координат оxyz незмінно пов'язаної з G. Положення G визначені в нерухливій системі координат радіусом-вектором М, а в рухливий - радіусом-вектором Початок рухливий системи координат - радіус-вектор ρ
З визначень твердого тіла й поступального руху випливає, що
При зміні часу визначають траєкторії М і О, причому ці траєкторії, згідно (12.1) можуть бути отримано одна з іншої паралельним переносом на постійний вектор
Точки М і О лежать на одному векторі Так як W=0, Е=0, то
Ці співвідношення слушні для будь-яких точок тіла G. Точка О називають полюсом, а її швидкість - швидкістю поступального руху твердого тіла використовуючи координатний спосіб завдання руху точки отримуємо:
(12.2) вказує, що рухаючись тіло володіє трьома ступенями волі. Якщо швидкість постійна, а прискорення дорівнює 0, то всі точки тіла рухаються рівномірно прямолінійно - прямолінійне рівномірне поступальне. Якщо швидкості всіх точок тіла рівні між собою, тільки в якійсь момент часу, то рух тіла - миттєво-поступальне.
Обертовий рух твердого тіла навколо нерухливої осі. Кінематичне рівняння руху. Кутова швидкість, прискорення Рух твердого тіла, що має дві нерухомі точки називається обертовий рух твердого тіла навколо нерухомої осі, а пряма минаюча осі - нерухливі осі обертання. Положення твердого тіла обертові навколо нерухливої осі визначається першим параметром кута повороту. Тобто дане тіло має перший ступінь волі. Кут Кожному моменту часу t відповідає певне значення кута повороту
(12.3) - кінематичне рівняння руху тв. тіла навколо нерухомої осі. Воно одночасно визначає закон обертового руху тіла навколо нерухливої осі. Кут
n-кількість оборотів тіла
Кутова швидкість тіла, що обертається навколо нерухливої осі рівна першій похідній за часом від кута повороту 𝝋 цього тіла й характеризує кінематичну міру зміни кута в часі.
У техніці кутову швидкість омега часто задають числом n - оборотів у хвилину. Зв'язок між омегою й Н:
Кутове прискорення тіла, що обертається навколо нерухливої осі дорівнює першій похідній від кутової швидкості, або другої від кута
При рівнозмінному обертовому русі, якщо ε більше 0 рух рівноприскорений, інакше рівносповільнене. Для рівнозмінного обертового руху тіла навколо нерухливої осі:
Якщо омега константа то обертання тіла рівномірне
Формула Ейлера Рис. 12.2 Нехай oxyz – рухлива система координат, незмінно пов’язана з тілом, вісь oz якої збігається з віссю обертання (рис12.3). Положення тіла G підраховуємо кутом 𝝋 щодо нерухливої система координат вісь від ζ якої збігається з віссю обертання тіла G. В цьому випадку орт К постійний, орти
Вектор омега, уведений по (12.11) завжди спрямований по осі обертання в ту сторону, звідки обертання тіла спостерігається, що відбуваються проти ходу годинної стрілки. Він визначає 3 елемента: 1. положення осі обертання тіла в нерухливій системі координат. 2. величину, що характеризує швидкість зміни кута повороту за одиницю часу 3. напрямок обертання тіла.
(12.12) - формула Ейлера Вона встановлює картину розподілення швидкостей точки тіла, що обертається навколо нерухливої осі. З формули (12.12) отримуємо:
Модуль швидкості будь-якої т. М дорівнює добутку модуля тіла на відстань R від М до осі обертання. Напрямлений вектор швидкості по дотичній до окружності, по якій рухається т. М. Тобто напрямок вектора швидкості визначається векторним добутком (12.12).
Плоско-паралельний рух Плоско-паралельним називається такий рух твердого тіла, при якому кожна його точка весь час рухається в одній площині, що паралельна деякій нерухомій площині, яка називається основною. Нерухома площина називається основною.
Рис. 12.3 Рис. 12.4 Для описання плоского руху потрібно три незалежні координати, як функції часу. Тобто, дане тіло володіє трьома степенями волі. Визначаємо положення плоскої фігури в площині рухомої системи oxy, незмінно зв’язаної з нерухомою Аξɳ (рис. 12.4) Розташування рухомої системи координат відносно нерухомої визначається координатами полюса Відповідно отримуємо рівняння (12.14)
Функція (12.4) – кінематичні рівняння плоско-паралельного руху.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.21 (0.006 с.) |



 .
. (12.1)
(12.1)



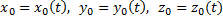 (12.2)
(12.2) - кут між двома площинами, що проходять через вісь обертання, одна з яких Q нерухлива відносно системи координат Аξηζ,а – інша Р незмінно пов'язана з даним тілом (рис. 11.2) Для визначення знака кута
- кут між двома площинами, що проходять через вісь обертання, одна з яких Q нерухлива відносно системи координат Аξηζ,а – інша Р незмінно пов'язана з даним тілом (рис. 11.2) Для визначення знака кута  (t) (12.3)
(t) (12.3) (12.5)
(12.5)
 (12.6)
(12.6)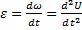 (12.7)
(12.7)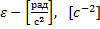
 (12.8)
(12.8) (12.9)
(12.9)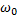 - початковий кут швидкості
- початковий кут швидкості (12.10)
(12.10) та
та  змінюються в напрямку
змінюються в напрямку  -
- ,
,  (12.11)
(12.11) (12.12)
(12.12) (12.13)
(12.13)
 , що співпадає з початком рухомої системи координат і кутом
, що співпадає з початком рухомої системи координат і кутом  (12.14)
(12.14)


