
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кінематика матеріальної точкиСодержание книги Поиск на нашем сайте
Положення матеріальної точки в просторі задається радіус-вектором: Середня швидкість руху частинки: де Миттєва швидкість частинки: де Модуль вектора швидкості: Закон додавання швидкостей Галілея: Середнє прискорення матеріальної точки:
де Миттєве прискорення матеріальної точки:
У проекціях на координатні вісі вектор прискорення:
де Модуль прискорення: Для рівномірного прямолінійного руху матеріальної точки (
Для рівноприскореного прямолінійного руху матеріальної точки ( Для криволінійного руху прискорення зручно представляти у вигляді двох взаємно ортогональних векторів:
де Середня кутова швидкість частинки:
де Миттєва кутова швидкість частинки:
Напрям вектора Середнє кутове прискорення частинки:
де Миттєве кутове прискорення
За прискореного обертання вектори Для рівномірного обертального руху Кінематичне рівняння обертального руху: а) рівномірного: б) рівнозмінного: Зв’язок між лінійними і кутовими величинами:
де У випадку обертального руху кутова швидкість дорівнює:
де Динаміка матеріальної точки Імпульс частинки:
де Закон руху частинки:
де Сили тертя. Пружні сили. Закон всесвітнього тяжіння. Сила тертя спокою:
де Сила тертя ковзання (закон Кулона-Амонтона):
де Сила тертя кочення:
де Сила пружності (закон Гука):
де Закон Гука для деформації розтягу (стиску):
де Руйнівна сила:
де Відносна зміна об’єму в разі повздовжньої деформації
де Коефіцієнт Пуассона:
де Закон Гука для деформації зсуву:
де Модуль Юнга
Кут закручення дротини:
де Потенціальна енергії пружної деформації розтягу(стиску):
де Закон всесвітнього тяжіння:
де Механіка твердого тіла Момент інерції матеріальної точки масою
де Момент інерції твердого тіла відносно вісі:
де Момент інерції: а) суцільного однорідного циліндра (диска) відносно вісі циліндра (диска):
де б) пустотілого циліндра (кільця) з внутрішнім радіусом
в) тонкостінного циліндра (тонкого кільця) радіуса
г) однорідного стрижня, що має довжину
д) однорідного стрижня, що має довжину
е) однорідної кулі масою
ж) куба, з ребром
Теорема Гюйгенса-Штейнера:
де Момент сили відносно деякої вісі
де Момент імпульсу твердого тіла відносно нерухомої вісі обертання
де Рівняння динаміки обертального руху твердого тіла навколо нерухомої вісі:
де Якщо момент інерції не змінюється, то
де
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.218.28 (0.011 с.) |

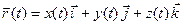 , де
, де 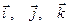 – одиничні вектори напрямів (орти);
– одиничні вектори напрямів (орти); 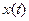 ,
,  ,
,  – координати точки, які можуть змінюватись з часом
– координати точки, які можуть змінюватись з часом  .
.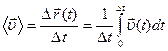 ,
, – переміщення точки,
– переміщення точки, 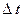 – інтервал часу, за який відбулося переміщення,
– інтервал часу, за який відбулося переміщення, 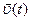 – миттєва швидкість частинки.
– миттєва швидкість частинки.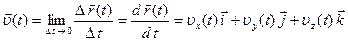 ,
,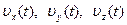 – проекції швидкості
– проекції швидкості 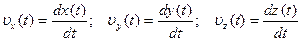 .
. .
.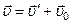 , де
, де  – швидкість матеріальної точки відносно нерухомої системи відліку (абсолютна швидкість),
– швидкість матеріальної точки відносно нерухомої системи відліку (абсолютна швидкість),  – швидкість точки відносно рухомої системи відліку (відносна швидкість),
– швидкість точки відносно рухомої системи відліку (відносна швидкість), 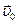 – швидкість рухомої системи відліку відносно нерухомої (переносна швидкість).
– швидкість рухомої системи відліку відносно нерухомої (переносна швидкість).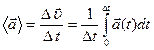 ,
,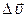 – приріст швидкості за час
– приріст швидкості за час 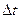 ,
,  – миттєве прискорення матеріальної точки.
– миттєве прискорення матеріальної точки.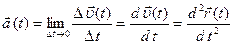 .
.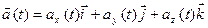 ,
,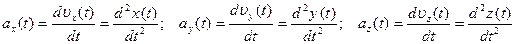 .
. .
.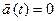 ):
): – рівняння руху;
– рівняння руху; 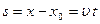 – шлях, який пройшла точка за час
– шлях, який пройшла точка за час  ):
): 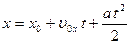 – рівняння руху;
– рівняння руху; 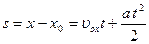 – шлях, який пройшла точка за час
– шлях, який пройшла точка за час 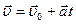 – швидкість точки.
– швидкість точки. ;
;  ;
;  ,
, – тангенціальне прискорення,
– тангенціальне прискорення,  – нормальне (доцентрове) прискорення,
– нормальне (доцентрове) прискорення, 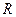 – локальний радіус кривизни траєкторії.
– локальний радіус кривизни траєкторії. ,
,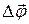 – кутове переміщення точки,
– кутове переміщення точки, 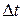 – інтервал часу, за який відбулося переміщення.
– інтервал часу, за який відбулося переміщення.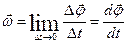 ,
, визначається за правилом правого гвинта: якщо гвинт обертати в напрямку руху частинки, то його поступальний рух покаже напрям кутового переміщення.
визначається за правилом правого гвинта: якщо гвинт обертати в напрямку руху частинки, то його поступальний рух покаже напрям кутового переміщення. ,
, – зміна кутової швидкості,
– зміна кутової швидкості, 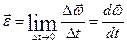 ,
, і
і 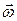 збігаються за напрямом; за сповільненого обертання вектори
збігаються за напрямом; за сповільненого обертання вектори  , тоді
, тоді 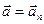 .
. ;
; ,
, ,
,  ,
, 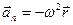 ,
, – радіус-вектор, проведений від миттєвого центра кривизни траєкторії до частинки.
– радіус-вектор, проведений від миттєвого центра кривизни траєкторії до частинки.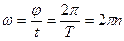 ,
, – частота обертання:
– частота обертання:  , (
, (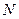 – число обертів за час
– число обертів за час 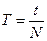 . Отже,
. Отже, 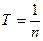 .
. . Імпульс системи частинок:
. Імпульс системи частинок: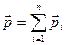 ,
, – імпульс
– імпульс 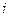 -ї частинки.
-ї частинки. ,
, – рівнодіюча всіх сил, що діють на частинку. За умови, що
– рівнодіюча всіх сил, що діють на частинку. За умови, що  , маємо
, маємо  .
. ,
, – сила тертя ковзання.
– сила тертя ковзання.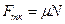 ,
,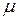 – коефіцієнт тертя ковзання,
– коефіцієнт тертя ковзання, 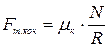 ,
, – коефіцієнт тертя кочення,
– коефіцієнт тертя кочення, 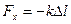 ,
, – коефіцієнт пружності,
– коефіцієнт пружності, 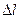 – абсолютна деформація тіла.
– абсолютна деформація тіла.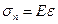 ,
,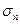 – нормальна механічна напруга (
– нормальна механічна напруга ( ),
),  – модуль Юнга,
– модуль Юнга,  – відносна повздовжня деформація (
– відносна повздовжня деформація ( ).
).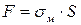 ,
,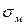 – межа міцності,
– межа міцності,  – площа поперечного перерізу тіла.
– площа поперечного перерізу тіла.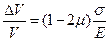 ,
,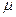 – коефіцієнт Пуассона.
– коефіцієнт Пуассона. ,
,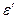 – відносна поперечна деформація (
– відносна поперечна деформація ( ),
),  – коефіцієнт поперечного стиснення внаслідок повздовжнього розтягу.
– коефіцієнт поперечного стиснення внаслідок повздовжнього розтягу. ,
,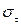 – тангенціальна механічна напруга,
– тангенціальна механічна напруга, 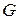 – модуль зсуву,
– модуль зсуву, 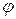 – кут зсуву.
– кут зсуву.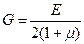 ,
,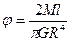 ,
,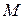 – крутильний момент,
– крутильний момент, 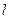 – довжина дротини,
– довжина дротини, 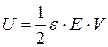 ,
, – об’єм тіла.
– об’єм тіла.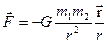 ,
, – гравітаційна стала,
– гравітаційна стала,  і
і  – маси взаємодіючих частинок,
– маси взаємодіючих частинок,  – вектор, який визначає положення другої частинки відносно першої.
– вектор, який визначає положення другої частинки відносно першої. , що обертається навколо вісі:
, що обертається навколо вісі: ,
,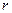 – відстань від точки до вісі.
– відстань від точки до вісі.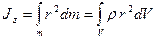 ,
, – густина тіла.
– густина тіла.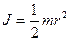 ,
,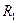 і зовнішнім радіусом
і зовнішнім радіусом 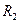 відносно вісі, що збігіється з віссю циліндра (кільця):
відносно вісі, що збігіється з віссю циліндра (кільця): ;
;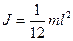 ;
;
 ;
;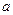 і масою
і масою 
 ,
,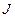 – момент інерції тіла відносно довільної вісі,
– момент інерції тіла відносно довільної вісі,  – момент інерції тіла відносно вісі, що проходить через центр мас і паралельна даній,
– момент інерції тіла відносно вісі, що проходить через центр мас і паралельна даній, 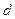 – відстань між вісями.
– відстань між вісями. :
: ,
, – проекція сили
– проекція сили  ,
,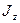 – момент інерції тіла відносно вісі
– момент інерції тіла відносно вісі  – кутова швидкість тіла.
– кутова швидкість тіла. ,
,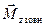 – геометрична сума моментів зовнішніх сил, що діють на тіло.
– геометрична сума моментів зовнішніх сил, що діють на тіло. ,
, – кутове прискорення (
– кутове прискорення (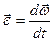 ).
).


