
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип Даламбера. Рівняння ЛагранжаСодержание книги
Поиск на нашем сайте
Повернімося до вивчення задач динаміки. Розглянемо принцип Даламбера, який тісно пов’язаний зі статикою і з її подальшим розвитком. Закони Ньютона встановлені для вільної матеріальної точки і вільної матеріальної системи. Між тим більшість матеріальних систем, з якими зустрічаємося на Землі, невільні. Наукові дослідження у XVIII і XIX ст. в області механіки були направлені на те, щоб розповсюдити закони руху, знайдені для вільних систем, на вивчення руху невільних систем. У працях вітчизняних вчених Я. Германа (1716 р.) і Л. Ейлера (1736 р.) були вказані методи, які дозволяють розв‘язувати задачі динаміки для невільних матеріальних систем. Незалежно від цих вчених декілька пізніше французький вчений Даламбер (1743 р.) сформулював принцип, який увійшов у механіку під назвою «принцип Даламбера». Доказ, запропонований Даламбером, був громіздкий, але він спростився у XIX столітті, коли була зформульована аксіома про звільнення від в’язей. Ми розглянули принцип віртуальних переміщень Розглянемо тепер так званий динамічний принцип віртуальних переміщень. Нехай на механічну систему n точок (рис. 11) накладено k голономних, утримуючих стаціонарних в'язей. Запишемо рівняння руху такої системи
тут
рис.11
Система (4.1) має 6n невідомих і складається з 3n рівнянь. Якщо до цієї системи додати k рівнянь в'язей
то отримаємо систему 3n+k рівнянь, за допомогою якої не можливо визначити 6n невідомих. Перепишемо (4.1) у вигляді
Даламбер назвав величину - при русі механічної системи активні сили і сили реакції в'язей у будь-який момент часу урівноважуються силами інерції Даламбера.
Розглянемо більш докладніше силу інерції. 1. Сила інерції направлена у сторону, протилежну прискоренню точки. 2. Сила інерції не прикладена до матеріальної точки. Якби вона була прикладена до точки, то точка б зупинилась. Виходячи з третього закону Ньютона можна зробити висновок, що сила інерції виникає внаслідок протидії точки. Крім цього можна показати, що 1) якщо точка системи знаходиться у взаємодії з декількома тілами, то реально існують складові сили інерції, а сама вона є фіктивною, дорівнює векторній сумі реальних сил, але прикладених до різних тіл. Якщо на точку діє одне тіло, то сила інерції, прикладена до цього тіла, є реальною; 2) так як сила інерції прикладена не до точки, а до в’язі, рівновага системи, що визначається рівняннями (4.3), уявна або фіктивна. Принцип Даламбера – простий наслідок законів Ньютона і аксіоми про звільнення від в’язів. Механіку можна побудувати і без принципу Даламбера, але він має велике практичне значення, так як дозволяє формально зводити задачі динаміки до задач статики, що суттєво спрощує їх розв’язання. Принцип Даламбера найбільш доцільно застосовувати при розв'язанні прямої задачі динаміки, коли невідомими величинами є сили. При розв’язанні оберненої задачі динаміки також можна застосовувати принцип Даламбера: він дозволяє дуже легко скласти диференціальні рівняння руху. Ця методика складання диференціальних рівнянь руху використовується у механіці суцільних середовищ: у теорії пружності, опору матеріалів, гідравліці і т.д. При цьому спочатку складають рівняння рівноваги, після того приписують силу інерції і отримують рівняння руху. Розглянемо приклади. Приклад 1. На тросі підвішений тягар М. Це може бути, наприклад, кабіна ліфту, прикріплена до тросу. Кабіна ліфту вагою Ропускається униз із прискоренням Розв’язання. Зробимо аналіз сил, прикладених до кабіни ліфту: сила ваги
Згідно із принципом Даламбера кабіна під дією сил Проведемо вісь
звідки знайдемо натяг тросу
Приклад 2. Два вантажі вагою

рис.12 рис.13 Розв’язання. Троси рухаються поступально, прискорення всіх точок тросів однакові. Якщо у місці контакту з блоком немає сковзання тросу, то прискорення дорівнює тангенціальному прискоренню при обертанні тіла навколо нерухомої осі
Знаючи прискорення вантажів знайдемо сили інерції
Складемо рівняння рівноваги за принципом Даламбера, прирівнявши до нуля суму моментів всіх сил відносно точки
Підставивши (d) у (e), отримаємо:
Звідси знайдемо
Цінність принципу Даламбера полягає в тому, що рівнянню динаміки (4.1) надано вигляду рівняння статики і, отже, завдання динаміки можуть вирішуватися як завдання статики. Помножимо (4.3) на віртуальне переміщення, підсумуємо по усіх точках і скористаємося визначенням ідеальних в'язей
це рівняння є записом динамічного принципу віртуальних переміщень: – якщо механічна система рухається під дією активних сил і на неї накладені голономні, утримуючі ідеальні в'язі, то у будь-який момент часу сума віртуальних робіт активних сил і сил інерції Даламбера дорівнює нулю. Рівняння (4.4) можна записати у вигляді
Динамічний принцип віртуальних переміщень отриманий Лагранжем з принципу Даламбера і носить назву принцип Даламбера-Лагранжа. Рівняння (4.4, 4.5) називаються також загальними рівняннями динаміки, оскільки з них можуть бути отримані рівняння руху будь-якої системи з голономними в'язями. Такі рівняння називаються рівняннями Лагранжа. Виведемо ці рівняння. Помітимо, що рівняння, які будуть зараз виведені, називаються рівняннями Лагранжа II роду. Але оскільки рівняння Лагранжа I роду не входять в програму, то ми їх не розглядаємо, а рівняння Лагранжа II роду називатимемо просто рівняннями Лагранжа.
Рівняння Лагранжа Розглянемо механічну систему n точок, на яку накладені k голономних ідеальних утримуючих стаціонарних в'язей. В цьому випадку рівняння Положення системи описуватимемо узагальненими координатами qs, кількість яких, як раніше відзначалося, дорівнює числу степенів вільності, а саме: 3n - k=l, тобто узагальнені координати qs і їх варіації Отримаємо тепер рівняння руху такої системи у вигляді системи рівнянь Лагранжа, яка дозволить знайти усі невідомі. Запишемо деякі попередні співвідношення. 1). Оскільки
величину
називають узагальненою швидкістю. Тоді (5.1) запишемо у виді
Скористаємося очевидними співвідношеннями
2).
3).
Запишемо принцип Даламбера-Лагранжа (4.4)
і підставимо в нього віртуальні переміщення системи
Змінимо порядок підсумовування
Величина
Розглянемо вираз
Звідки
або з урахуванням (4.5) і (5.4)
тоді (*) перепишемо у виді
або
s=1, 2, 3,., l,
де Рівняння (5.6) і є рівняннями Лагранжа, їх всього 3n - k, тобто стільки, скільки незалежних координат. Невідомими в них є q=q(t), потім можна (якщо потрібно) знайти Помітимо, що якщо в якості узагальнених координат вибрати інші координати
Такі перетворення називають точковими. На закінчення розглянемо приклад використання рівнянь Лагранжа. Визначити період коливань математичного маятника завдовжки l. Положення маятника однозначно визначається його координатами x і y, але вони не є незалежними, оскільки можуть бути виражені через l і
Активна сила
Знаходимо повну похідну
Знаходимо частинну похідну
Рівняння Лагранжа набуде тепер вигляду
де Розв’язком такого рівняння, як відомо, є
тобто маятник здійснюватиме гармонійні коливання з періодом
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.138.124 (0.012 с.) |

 в декартових координатах або
в декартових координатах або 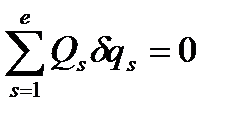 в узагальнених координатах, за допомогою якого зформулювали необхідні та достатні умови рівноваги механічної системи. Тому цей принцип називається статичним принципом. Він лежить в основі статики.
в узагальнених координатах, за допомогою якого зформулювали необхідні та достатні умови рівноваги механічної системи. Тому цей принцип називається статичним принципом. Він лежить в основі статики. (4.1)
(4.1) - векторна сума внутрішніх і зовнішніх сил, діючих на i - ту точку,
- векторна сума внутрішніх і зовнішніх сил, діючих на i - ту точку,  - сумарна реакція сил в'язей, діючих на i - ту точку.
- сумарна реакція сил в'язей, діючих на i - ту точку.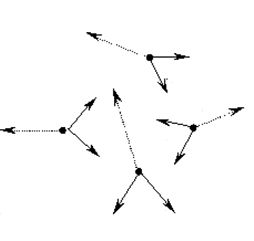
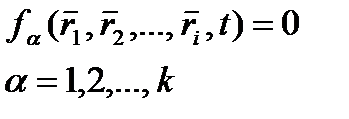 (4.2)
(4.2)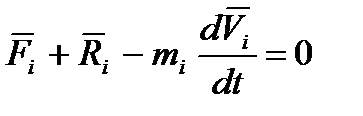 (4.3)
(4.3)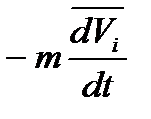 силою інерції (пізніше її назвали силою інерції Даламбера) і сформулював принцип, що дістав назву принципа Даламбера:
силою інерції (пізніше її назвали силою інерції Даламбера) і сформулював принцип, що дістав назву принципа Даламбера: . Потрібно знайти натяг тросу Т(рис. 12).
. Потрібно знайти натяг тросу Т(рис. 12). , натяг
, натяг 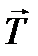 і умовно вважаємо прикладеною силу інерції рівною
і умовно вважаємо прикладеною силу інерції рівною .
. повинна знаходитися у рівновазі. Всі сили діють по прямій, тому достатньо скласти одне рівняння рівноваги.
повинна знаходитися у рівновазі. Всі сили діють по прямій, тому достатньо скласти одне рівняння рівноваги. , обравши її початок у закріпленій точці
, обравши її початок у закріпленій точці  . Прирівняємо до нуля суму проекцій всіх сил на вісь
. Прирівняємо до нуля суму проекцій всіх сил на вісь  ,
,
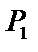 і
і 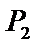 підвішені до тросів подвійного блоку (рис.13). Припустимо, що
підвішені до тросів подвійного блоку (рис.13). Припустимо, що 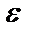 , з яким буде обертатися блок. Масу блока при цьому не враховувати. Радіуси блоків
, з яким буде обертатися блок. Масу блока при цьому не враховувати. Радіуси блоків 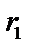 і
і  .
.
 ;
; 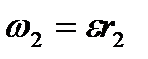 . (c)
. (c)
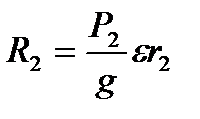 (d)
(d)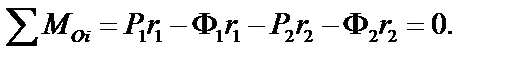 (e)
(e) . (f)
. (f)
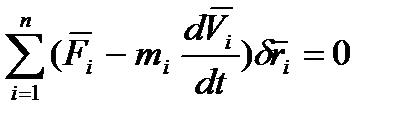 (4.4)
(4.4) (4.5)
(4.5) містить 6n невідомих 3n проекцій
містить 6n невідомих 3n проекцій 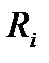 і 3n координат. З них 3n - k координат є невідомими, інші k визначаються з рівняння в'язі. Таким чином, кількість невідомих більша, ніж кількість рівнянь.
і 3n координат. З них 3n - k координат є невідомими, інші k визначаються з рівняння в'язі. Таким чином, кількість невідомих більша, ніж кількість рівнянь.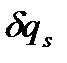 є незалежними і їх можна задавати довільним чином.
є незалежними і їх можна задавати довільним чином.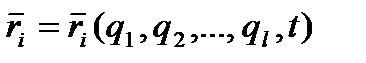 , то
, то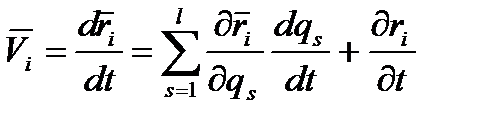 (5.1)
(5.1) (5.2)
(5.2) (5.3)
(5.3)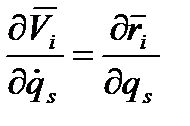 (5.4)
(5.4) (5.5)
(5.5)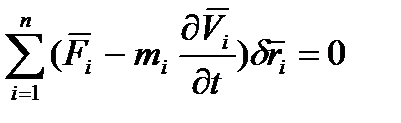
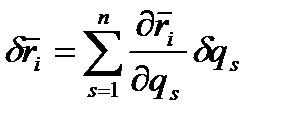 , отримаємо
, отримаємо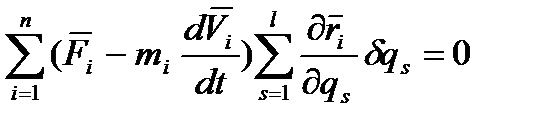

 називається силою, що відповідає узагальненій координаті qs. Враховуючи, що
називається силою, що відповідає узагальненій координаті qs. Враховуючи, що 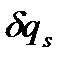 - незалежні варіації узагальнених координат, то ліва частина дорівнює нулю, якщо
- незалежні варіації узагальнених координат, то ліва частина дорівнює нулю, якщо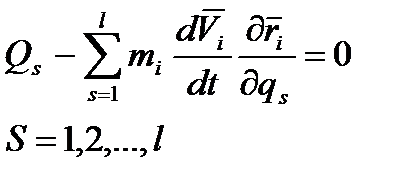 (*)
(*)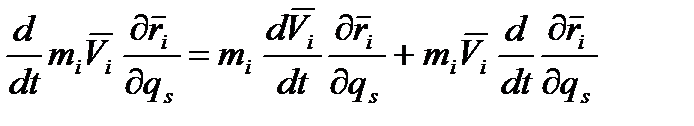 ,
,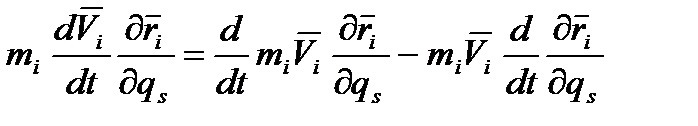
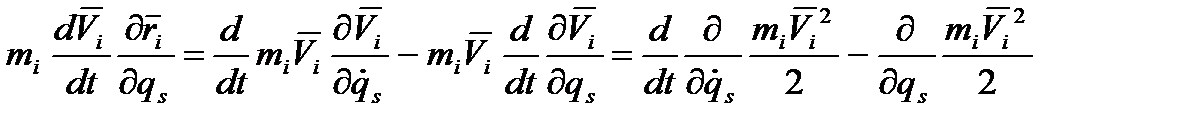 ,
,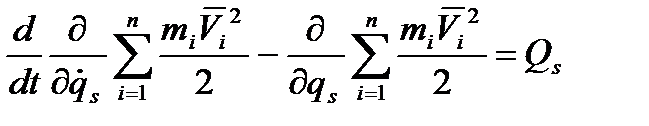
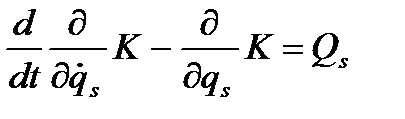 (5.6)
(5.6)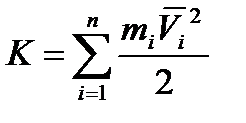 - кінетична енергія системи.
- кінетична енергія системи. . Знаючи
. Знаючи 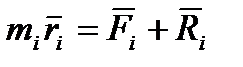 знайти реакції в'язей, тобто розв’язати основну задачу динаміки пов'язаних систем.
знайти реакції в'язей, тобто розв’язати основну задачу динаміки пов'язаних систем.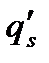 , так що
, так що 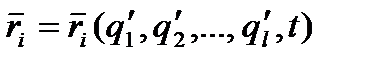 , то зробивши такі самі викладення, як ми зробили, отримаємо рівняння Лагранжа у вигляді
, то зробивши такі самі викладення, як ми зробили, отримаємо рівняння Лагранжа у вигляді 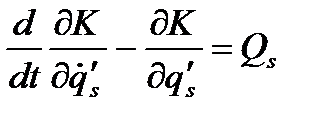 , отже, рівняння Лагранжа не змінює вигляду при зміні узагальнених координат, тобто є інваріантним відносно перетворень
, отже, рівняння Лагранжа не змінює вигляду при зміні узагальнених координат, тобто є інваріантним відносно перетворень .
.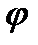 , тому незалежною є тільки одна координата і для визначення положення маятника досить задати одну узагальнену координату - це може бути кут
, тому незалежною є тільки одна координата і для визначення положення маятника досить задати одну узагальнену координату - це може бути кут 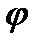 , тобто
, тобто 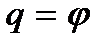 . Тоді і рівняння Лагранжа буде одне. Запишемо вираз для кінетичної енергії
. Тоді і рівняння Лагранжа буде одне. Запишемо вираз для кінетичної енергії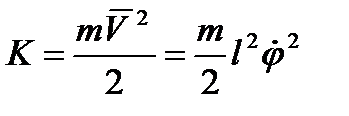 .
.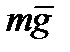 є потенціальною. Тому узагальнену силу, що відповідає узагальненій координаті
є потенціальною. Тому узагальнену силу, що відповідає узагальненій координаті 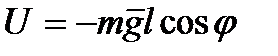 по узагальненій координаті, тобто
по узагальненій координаті, тобто 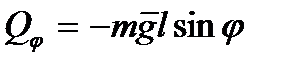 . Рівняння Лагранжа матиме вигляд
. Рівняння Лагранжа матиме вигляд .
.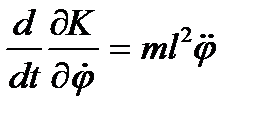 .
. .
.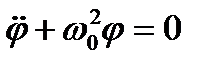 ,
,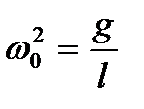 і
і 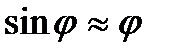 для малих коливань.
для малих коливань. ,
, .
.


