
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завражна О.М., Мороз І.О., Лобас О.М.Содержание книги
Поиск на нашем сайте
Завражна О.М., Мороз І.О., Лобас О.М. М 80 Аналітична механіка: навчально-методичний посібник. – Суми: Видавництво СумДПУ імені А.С. Макаренка, 2015. -100 с.
У навчально-методичному посібнику розглянуті основні положення аналітичної механіки, розроблені методичні рекомендації до розв’язування найбільш типових задач, приводяться приклади розв’язування таких задач, дано порівняльний аналіз методів аналітичної фізики та підібраний список завдань для самостійної роботи. Посібник пропонується для студентів фізичних та інших спеціальностей педагогічних університетів. Він може бути корисним для студентів інших навчальних закладів які вивчають класичну механіку як предмет у всіх його аспектах. Матеріал навчально-методичного посібника за своїм змістом та структурою повністю відповідає сучасним стандартам фізичної освіти для педагогічних спеціальностей.
Зміст
ВСТУП- 6 РОЗДІЛ 1. ОСНОВНІ ПОЛОЖЕННЯ АНАЛІТИЧНОЇ МЕХАНІКИ 7 §1.1 В'язі. Класифікація в'язей. Основне завдання динаміки пов'язаних механічних систем- 8 §1.2 Можливі, дійсні та віртуальні переміщення- 11 §1.3 Узагальнені координати. Узагальнені сили. Принцип віртуальних переміщень 13 §1.4 Принцип Даламбера. Рівняння Лагранжа 27 §1.5 Рівняння Лагранжа 32 §1.6 Структура рівнянь Лагранжа для різних класів механічних систем 36 §1.7 Структура функції Лагранжа для системи з потенціальними й узагальнено - потенціальними силами- 40 §1.8 Зв'язок функції Лагранжа із законом збереження енергії 42 §1.9 Циклічні координати й узагальнені імпульси- 44 §1.10 Канонічне рівняння руху. Дужки Пуассона 47 §1.11 Рівняння Гамільтона. Принцип Гамільтона. Дві системи побудови класичної механіки- 51 РОЗДІЛ ІІ. ВИКОРИСТАННЯ ОСНОВНИХ ПОЛОЖЕНЬ МЕХАНІКИ ЛАГРАНЖА ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ ДИНАМІКИ- 54 §2.1 Застосування методу кінетостатики- 58 §2.2 Використання принципу можливих переміщень для розв’язання задач 64 §2.3 Застосування загального рівняння динаміки системи матеріальних точок 68 §2.4 Обчислення узагальнених координат та узагальнених сил 73 §2.5 Застосування рівняння Лагранжа 76 §2.6 Розв’язання задач з використанням рівнянь Гамільтона 85 РОЗДІЛ ІІІ. ПОРІВНЯЛЬНИЙ АНАЛІЗ МЕТОДІВ РОЗВ’ЯЗАННЯ 91 Завдання на розрахунково-графічні роботи з теоретичної механіки 93 Література- 98 ВСТУП Усе реально існуюче у світі, починаючи від елементарних частинок і різних полів, від атомів та молекул і закінчуючи такими об'єктами Всесвіту, як зірки та галактики, є єдиною матеріальною системою, що знаходяться в стані безперервного руху і зміни. Форми руху матеріальних об'єктів дуже різноманітні та багаточисельні. Найбільш простою формою руху є механічний рух. Теорією, яка описує цей рух, є класична механіка Ньютона, що існує вже близько трьохсот років. Основу класичної механіки складає велика кількість порівняно простих та наочних гіпотез (постулатів), що пов'язані з введенням основних понять про простір та час, сили та маси, інерціальні системи відліку та закони Ньютона. Проте при розв’язанні задач динаміки часто виникають затруднення, пов'язані з вибором відповідних теорем та рівнянь. Багато завдань динаміки неможливо розв’язати використовуючи механіку Ньютона, оскільки доводитися складати систему диференціальних рівнянь, які не завжди можна проінтегрувати. У деяких завданнях можливе застосування наближених методів розв’язання, але точний результат ми не можемо отримати. Щоб уникнути інтеграції системи диференціальних рівнянь, необхідно застосувати до розв’язання задач методи аналітичної фізики. До них відносяться: метод кінетостатики, принцип можливих переміщень, рівняння Лагранжа та Гамільтона, загальне рівняння динаміки пов'язаних систем. Завдання даної роботи: 1. розробити алгоритми розв’язання типових завдань (динаміки системи тіл) цими методами; 2. дати порівняльний аналіз розв’язань типових завдань динаміки методами аналітичної фізики та зіставити їх із механікою Ньютона. Робота складається з трьох розділів, містить задачі для самостійного розв’язання, список літератури: - у першому розділі розглядаються основні положення аналітичної механіки Лагранжа, Гамільтона. - у другому наводяться розв’язки за допомогою методів аналітичної фізики і алгоритми розв’язання задач. - у третьому розділі дано порівняльний аналіз методів аналітичної фізики. РОЗДІЛ 1. ОСНОВНІ ПОЛОЖЕННЯ АНАЛІТИЧНОЇ МЕХАНІКИ
Класична механіка, основні положення якої були сформульовані Галілеєм, Ньютоном, отримала подальший розвиток в дослідженнях Даламбера, Лагранжа, Гамільтона, Якобі, Остроградского та інших вчених, які розробили загальні аналітичні прийоми розв’язання задач механіки як вільних, так і невільних механічних систем. В результаті цих досліджень було встановлено найбільш загальний принцип класичної механіки − інтегральний варіаційний принцип Гамільтона - Остроградского. За означенням Ж. Лагранжа, розділ аналітична механіка є сукупністю найбільш загальних аналітичних методів розв'язання задач механіки вільних і невільних матеріальних систем, що не ґрунтуються на наочних геометричних уявленнях, які використовував ще І. Ньютон. У сучасній аналітичній механіці аналітичні методи і геометричні образи настільки взаємопов'язані, що не може бути і мови про їх відокремлення. Основою аналітичної механіки є три групи фундаментальних положень. ü До першої групи слід віднести варіаційні принципи, які в простій інваріантній формі містять формулювання найбільш загальних закономірностей механіки. ü Друга група фундаментальних положень об'єднує диференціальні рівняння руху механічних систем, які є наслідком варіаційних принципів. ü Третя група об'єднує загальні методи інтегрування рівнянь динаміки. Основоположними поняттями аналітичної механіки є: o уявлення про в'язі та їх класифікація; o поняття про дійсні й можливі переміщення.
Узагальнені координати. Узагальнені сили. Принцип віртуальних переміщень
Байдуже
рис.10.в
При виведенні тіла з положення рівноваги його потенціальна енергія не змінюється (мал. 10. в). Сідлоподібне
рис. 10.г Рівновага залежить від напряму зрушення.
Рівняння Лагранжа Розглянемо механічну систему n точок, на яку накладені k голономних ідеальних утримуючих стаціонарних в'язей. В цьому випадку рівняння Положення системи описуватимемо узагальненими координатами qs, кількість яких, як раніше відзначалося, дорівнює числу степенів вільності, а саме: 3n - k=l, тобто узагальнені координати qs і їх варіації Отримаємо тепер рівняння руху такої системи у вигляді системи рівнянь Лагранжа, яка дозволить знайти усі невідомі. Запишемо деякі попередні співвідношення. 1). Оскільки
величину
називають узагальненою швидкістю. Тоді (5.1) запишемо у виді
Скористаємося очевидними співвідношеннями
2).
3).
Запишемо принцип Даламбера-Лагранжа (4.4)
і підставимо в нього віртуальні переміщення системи
Змінимо порядок підсумовування
Величина
Розглянемо вираз
Звідки
або з урахуванням (4.5) і (5.4)
тоді (*) перепишемо у виді
або
s=1, 2, 3,., l,
де Рівняння (5.6) і є рівняннями Лагранжа, їх всього 3n - k, тобто стільки, скільки незалежних координат. Невідомими в них є q=q(t), потім можна (якщо потрібно) знайти Помітимо, що якщо в якості узагальнених координат вибрати інші координати
Такі перетворення називають точковими. На закінчення розглянемо приклад використання рівнянь Лагранжа. Визначити період коливань математичного маятника завдовжки l. Положення маятника однозначно визначається його координатами x і y, але вони не є незалежними, оскільки можуть бути виражені через l і
Активна сила
Знаходимо повну похідну
Знаходимо частинну похідну
Рівняння Лагранжа набуде тепер вигляду
де Розв’язком такого рівняння, як відомо, є
тобто маятник здійснюватиме гармонійні коливання з періодом
З теоретичної механіки
Дослідження руху системи материальних точок проводяться комплексно, шляхом використання різних методів для визначення основних характеристик руху конкретної механічної системи абсолютно твердих тіл під дією постійних сил ваги. Такий підхід дозволяє, крім тривіального надання навиків використання теорії для практичних розрахунків та їх закріплення, розв'зати також дуже важливу проблему аналізу одержаних різними методами результатів розв'язку однієї задачі динаміки. Це дає можливість порівняти різні шляхи розв'язання однієї задачі і перевірити правильність отриманих результатів.
Умови завдання
Механічна система (механізм), яка складена з декількох абсолютно твердих тіл, починає рухатися з стану спокою під дією сил ваги. Вважаючи в'язі ідельними і нехтуючи їх масами визначити в мить часу, коли тіло А пройде шлях S, величини які вказані в пунктах 1, 2, 3,4, 5 завдання. Схеми механічних систем показані на рис. 26. В завданні прийняті слідуючи позначення: mA, mB, mБ, mД - маси тіл А, В, Б, Д; Rв=2rв, RД=1,5rД - радіуси великих і малих кіл; івх, ідх - радіуси інерції тіл В і Д, відносно горизонтальних осей, що проходять через їх центри мас, a, b - кути нахилу площин до горизонту; m - коефіцієнт тертя тіла А. Необхідні дані приведені в таблиці 1. СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 1. Жирнов Н.И. Классическая механика. – М.: Просвещение, 1980. – 303 с. 2. Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. - М.: Высш. шк., 1974. - 528 с. 3. Мултановский В. В., Василевский А. С. Курс теоретической физики. Том 3. Квантовая механика. М.: Просвещение, 1991, 320 с. 4. Кільчевский М. О. Курс теоретичної механіки. - К.: "Радянська школа", 1950. - Ч. І і ІІ. 5. Воронков И.М. Курс теоретической механики. - М.: Наука, 1966. -. 596 с. 6. Тарг С.М. "Краткий курс теоретической механики. Москва, Высшая школа, 1986 - 416с 7. Голубева О.В. Теоретическая механика Высшая школа, 1968 8. Федорченко А.М. Теоретична фізика. Механіка DJVU. Раздел: Физика → Механика. "Вища школа" 1971, 272 с. 9. Бухгольц Н.Н. Основной курс теоретической механики М.: Наука, 1965. – 468 с. 10. Иос Г. Курс теоретической физики. - М.: Учпедгиз, 1963. 11. Компанеец А. С. Теоретическая физика. М.: Наука, 1957. -563 с. 12. Яблонский А.А., Никифорова В.М. Курс теоретической механики. -Ч. 1,2 - М.: Высш. шк., 1984. 13. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Том 2: Динамика (3-е издание). М.: Наука, 1966. - 663 с 14. Балаш В.А. Задачи по физике и методы их решения: пособие для учителей [Текст] / В.А. Балаш – М.: Просвещение, 1974. – 430 с. 15. Мещерский, И. В. Сборник задач по теоретической механике: учеб. пособие для вузов / И. В. Мещерский; под ред. Н. В. Бутенина, А. И. Лурье, Д. Р. Меркина. - 33-е изд., стереотип. - М.: Наука, 1973. - 448 с. 16. Осадчий В. А., Файн А. М. Руководство к решению задач по теоретической механике. “Высшая школа”, М., 1966. 17. Аркуша А.И. Руководство к решению задач по теоретической механике - М.: Высшая школа, 1971. -296 с 18. Сборник заданий для курсовых работ по теоретической механике. Под ред. А.А. Яблонского. - Учебное пособие для вузов. – 4-е изд., перераб. и доп. – М.: Высшая школа, 1985. - 367с.. 19. Файн А.М. Сборник задач по теоретической механике. - М.: Высш. школа, 1978. - 189 с.
Навчальне видання
О.М. Завражна, І.О. Мороз, О.М. Лобас
АНАЛІТИЧНА МЕХАНІКА
Здано в набір 15.05.2015. підписано до друку 28.05.2015. Формат 60×84/16. Гарн. Times New Roman. Друк ризогр. Ум. друк. арк. 4. Тираж – 100
Вид-во СумДПУ імені А.С. Макаренка 40002 м. Суми, вул.. Роменська, 87
Виготовлено на обладнанні СумДПУ ім.. А.С. Макаренка
[1] Н.И. Жирнов, Класична механіка. М. "Освіта", 1980. Завражна О.М., Мороз І.О., Лобас О.М. М 80 Аналітична механіка: навчально-методичний посібник. – Суми: Видавництво СумДПУ імені А.С. Макаренка, 2015. -100 с.
У навчально-методичному посібнику розглянуті основні положення аналітичної механіки, розроблені методичні рекомендації до розв’язування найбільш типових задач, приводяться приклади розв’язування таких задач, дано порівняльний аналіз методів аналітичної фізики та підібраний список завдань для самостійної роботи. Посібник пропонується для студентів фізичних та інших спеціальностей педагогічних університетів. Він може бути корисним для студентів інших навчальних закладів які вивчають класичну механіку як предмет у всіх його аспектах. Матеріал навчально-методичного посібника за своїм змістом та структурою повністю відповідає сучасним стандартам фізичної освіти для педагогічних спеціальностей.
Зміст
ВСТУП- 6 РОЗДІЛ 1. ОСНОВНІ ПОЛОЖЕННЯ АНАЛІТИЧНОЇ МЕХАНІКИ 7 §1.1 В'язі. Класифікація в'язей. Основне завдання динаміки пов'язаних механічних систем- 8 §1.2 Можливі, дійсні та віртуальні переміщення- 11 §1.3 Узагальнені координати. Узагальнені сили. Принцип віртуальних переміщень 13 §1.4 Принцип Даламбера. Рівняння Лагранжа 27 §1.5 Рівняння Лагранжа 32 §1.6 Структура рівнянь Лагранжа для різних класів механічних систем 36 §1.7 Структура функції Лагранжа для системи з потенціальними й узагальнено - потенціальними силами- 40 §1.8 Зв'язок функції Лагранжа із законом збереження енергії 42 §1.9 Циклічні координати й узагальнені імпульси- 44 §1.10 Канонічне рівняння руху. Дужки Пуассона 47 §1.11 Рівняння Гамільтона. Принцип Гамільтона. Дві системи побудови класичної механіки- 51 РОЗДІЛ ІІ. ВИКОРИСТАННЯ ОСНОВНИХ ПОЛОЖЕНЬ МЕХАНІКИ ЛАГРАНЖА ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ ДИНАМІКИ- 54 §2.1 Застосування методу кінетостатики- 58 §2.2 Використання принципу можливих переміщень для розв’язання задач 64 §2.3 Застосування загального рівняння динаміки системи матеріальних точок 68 §2.4 Обчислення узагальнених координат та узагальнених сил 73 §2.5 Застосування рівняння Лагранжа 76 §2.6 Розв’язання задач з використанням рівнянь Гамільтона 85 РОЗДІЛ ІІІ. ПОРІВНЯЛЬНИЙ АНАЛІЗ МЕТОДІВ РОЗВ’ЯЗАННЯ 91 Завдання на розрахунково-графічні роботи з теоретичної механіки 93 Література- 98 ВСТУП Усе реально існуюче у світі, починаючи від елементарних частинок і різних полів, від атомів та молекул і закінчуючи такими об'єктами Всесвіту, як зірки та галактики, є єдиною матеріальною системою, що знаходяться в стані безперервного руху і зміни. Форми руху матеріальних об'єктів дуже різноманітні та багаточисельні. Найбільш простою формою руху є механічний рух. Теорією, яка описує цей рух, є класична механіка Ньютона, що існує вже близько трьохсот років. Основу класичної механіки складає велика кількість порівняно простих та наочних гіпотез (постулатів), що пов'язані з введенням основних понять про простір та час, сили та маси, інерціальні системи відліку та закони Ньютона. Проте при розв’язанні задач динаміки часто виникають затруднення, пов'язані з вибором відповідних теорем та рівнянь. Багато завдань динаміки неможливо розв’язати використовуючи механіку Ньютона, оскільки доводитися складати систему диференціальних рівнянь, які не завжди можна проінтегрувати. У деяких завданнях можливе застосування наближених методів розв’язання, але точний результат ми не можемо отримати. Щоб уникнути інтеграції системи диференціальних рівнянь, необхідно застосувати до розв’язання задач методи аналітичної фізики. До них відносяться: метод кінетостатики, принцип можливих переміщень, рівняння Лагранжа та Гамільтона, загальне рівняння динаміки пов'язаних систем. Завдання даної роботи: 1. розробити алгоритми розв’язання типових завдань (динаміки системи тіл) цими методами; 2. дати порівняльний аналіз розв’язань типових завдань динаміки методами аналітичної фізики та зіставити їх із механікою Ньютона. Робота складається з трьох розділів, містить задачі для самостійного розв’язання, список літератури: - у першому розділі розглядаються основні положення аналітичної механіки Лагранжа, Гамільтона. - у другому наводяться розв’язки за допомогою методів аналітичної фізики і алгоритми розв’язання задач. - у третьому розділі дано порівняльний аналіз методів аналітичної фізики.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |



 містить 6n невідомих 3n проекцій
містить 6n невідомих 3n проекцій 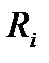 і 3n координат. З них 3n - k координат є невідомими, інші k визначаються з рівняння в'язі. Таким чином, кількість невідомих більша, ніж кількість рівнянь.
і 3n координат. З них 3n - k координат є невідомими, інші k визначаються з рівняння в'язі. Таким чином, кількість невідомих більша, ніж кількість рівнянь.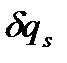 є незалежними і їх можна задавати довільним чином.
є незалежними і їх можна задавати довільним чином.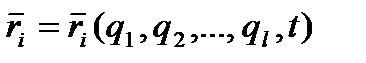 , то
, то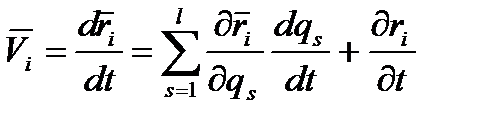 (5.1)
(5.1) (5.2)
(5.2) (5.3)
(5.3)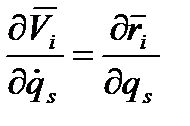 (5.4)
(5.4) (5.5)
(5.5)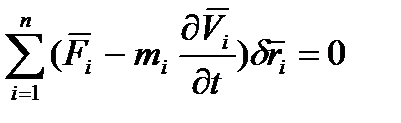
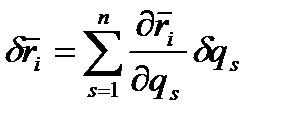 , отримаємо
, отримаємо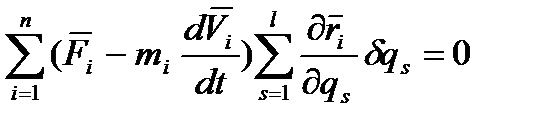

 називається силою, що відповідає узагальненій координаті qs. Враховуючи, що
називається силою, що відповідає узагальненій координаті qs. Враховуючи, що 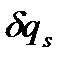 - незалежні варіації узагальнених координат, то ліва частина дорівнює нулю, якщо
- незалежні варіації узагальнених координат, то ліва частина дорівнює нулю, якщо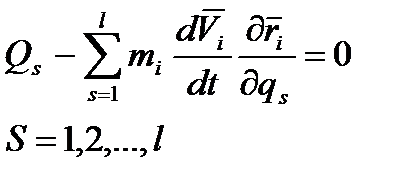 (*)
(*)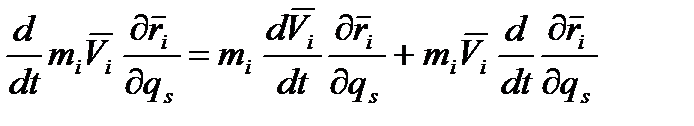 ,
,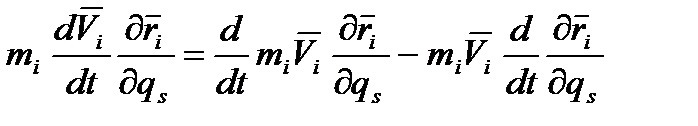
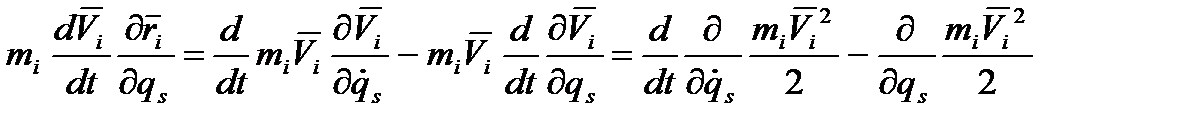 ,
,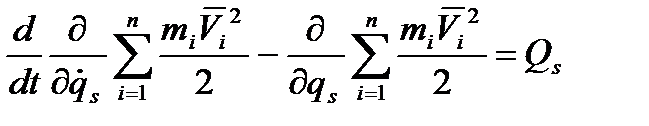
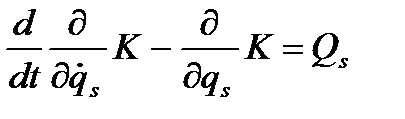 (5.6)
(5.6)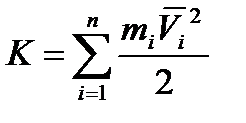 - кінетична енергія системи.
- кінетична енергія системи. . Знаючи
. Знаючи 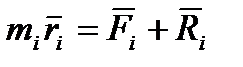 знайти реакції в'язей, тобто розв’язати основну задачу динаміки пов'язаних систем.
знайти реакції в'язей, тобто розв’язати основну задачу динаміки пов'язаних систем.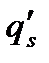 , так що
, так що 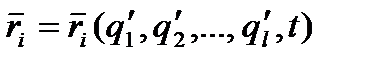 , то зробивши такі самі викладення, як ми зробили, отримаємо рівняння Лагранжа у вигляді
, то зробивши такі самі викладення, як ми зробили, отримаємо рівняння Лагранжа у вигляді 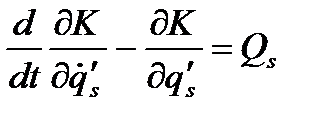 , отже, рівняння Лагранжа не змінює вигляду при зміні узагальнених координат, тобто є інваріантним відносно перетворень
, отже, рівняння Лагранжа не змінює вигляду при зміні узагальнених координат, тобто є інваріантним відносно перетворень .
.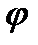 , тому незалежною є тільки одна координата і для визначення положення маятника досить задати одну узагальнену координату - це може бути кут
, тому незалежною є тільки одна координата і для визначення положення маятника досить задати одну узагальнену координату - це може бути кут 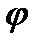 , тобто
, тобто 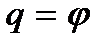 . Тоді і рівняння Лагранжа буде одне. Запишемо вираз для кінетичної енергії
. Тоді і рівняння Лагранжа буде одне. Запишемо вираз для кінетичної енергії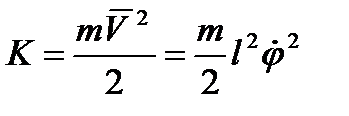 .
.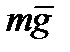 є потенціальною. Тому узагальнену силу, що відповідає узагальненій координаті
є потенціальною. Тому узагальнену силу, що відповідає узагальненій координаті 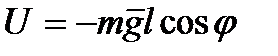 по узагальненій координаті, тобто
по узагальненій координаті, тобто 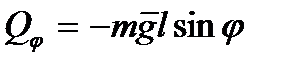 . Рівняння Лагранжа матиме вигляд
. Рівняння Лагранжа матиме вигляд .
.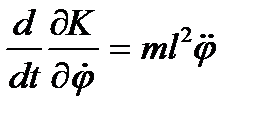 .
. .
.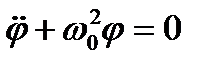 ,
,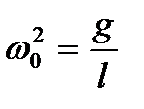 і
і 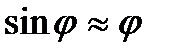 для малих коливань.
для малих коливань. ,
, .
.


