
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування загального рівняння динаміки системи матеріальних точокСодержание книги
Поиск на нашем сайте
При русі системи матеріальних точок, що підпорядкована ідеальним в'язям, сума заданих сил та сил інерції на будь-яких можливих переміщеннях точок системи дорівнює нулю:
Якщо
то загальне рівняння динаміки має вигляд
Загальне рівняння динаміки є аналогом принципу можливих переміщень для випадку руху системи матеріальних точок. Якщо не всі в’язі є ідеальними, то застосовуючи загальне рівняння динаміки пов’язаних систем, слід до сил, що задаються, додати сили реакцій, що відповідають неідеальним в’язям. Знаходження суми робіт сил інерції на можливих переміщеннях точок твердого тіла виконується за допомогою по формул: а) При поступальному русі:
де б) При обертанні навколо нерухомої вісі:
де в) При плоскому русі:
де За допомогою загального рівняння динаміки можна розв’язувати задачі динаміки систем матеріальних точок у випадках, коли до числа заданих величин і шуканих входять: - інерціональні характеристики (маси і моменти інерції), - прискорення точок системи (лінійні і кутові), - задані сили і пари сил, - коефіцієнти тертя (ковзання і кочення), - коефіцієнти пружності пружин.
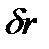 
    рис.20
1. Зобразимо задані сили 2. Додамо силу тертя ковзання 3. Додамо сили інерції матеріальних точок системи. Нехай вантаж В рухається вниз з шуканим прискоренням
4. До блоку С, що обертається навколо нерухомої вісі, прикладемо головний момент сил інерції
Головний вектор сил інерції блоку 5. Надамо вантажу А можливе переміщення 6. Залежність між лінійним і кутовим переміщеннями
Складемо для цієї системи загальне рівняння динаміки.
Так як то
Та визначимо шукане прискорення:
Аналізуючи розв’язання можна скласти наступний алгоритм: 1. Зобразити задані сили. 2. Зобразити сили реакцій, що відповідають неідеальним в’язям. 3. Визначити головні вектори і головні моменти сил інерції системи. а) Для систем з одним степенем вільності: 4. Надати можливого переміщення одній з точок системи і виразити можливі переміщення точок прикладання всіх сил, вказаних в перших 3-х пунктах, в залежності від заданого можливого переміщення. 5. Обчислити суму робіт всіх сил, вказаних в перших 3-х пунктах, на можливих переміщеннях точок системи. Скласти загальне рівняння динаміки і прирівняти отриману суму робіт сил до нуля. 6. Після скорочення складеного рівняння на задане можливе переміщення, визначити шукану величину або провести інтегрування диференціального рівняння. б) Для системи з декількома степенями вільності: 4. Надати можливі переміщення в кількості, що дорівнюють числу степенів вільності даної системи; 5. Обчислити можливі переміщення точок прикладання всіх сил, вказаних в перших 3-х пунктах, в залежності від кожного із заданих незалежних можливих переміщень. 6. Скласти систему рівнянь, число яких дорівнює числу степенів вільності даної системи. Кожне з одержаних рівнянь відповідає одному з незалежних можливих переміщень. При цьому всі останні можливі переміщення слід вважати рівними нулю. Для складання рівняння потрібно обчислити суму робіт всіх сил на можливих переміщеннях точок системи, які відповідають даному незалежному можливому переміщенню. Отриману роботу сил слід прирівняти до нуля.
7. Після скорочення кожного зі складених рівнянь на відповідне незалежне можливе переміщення потрібно визначити з одержаної системи рівнянь шукані величини або провести інтегрування системи диференціальних рівнянь руху.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.35.114 (0.007 с.) |

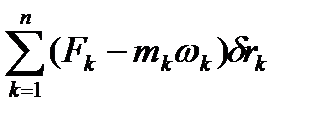

 ,
, ,
, .
.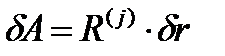 ,
, - рівнодійна сил інерції (
- рівнодійна сил інерції ( ,
,  - прискорення будь-якої точки твердого тіла),
- прискорення будь-якої точки твердого тіла),  - можливе переміщення будь-якої точки тіла.
- можливе переміщення будь-якої точки тіла. ,
, - головний момент сил інерції відносно осі обертання
- головний момент сил інерції відносно осі обертання  (
( ,
,  – момент інерції твердого тіла),
– момент інерції твердого тіла),  ,
, - головний вектор сил інерції (
- головний вектор сил інерції ( ,
,  - прискорення центру тяжіння твердого тіла),
- прискорення центру тяжіння твердого тіла),  - головний момент сил інерції відносно вісі, що проходить через центр тяжіння С твердого тіла перпендикулярного до площини його матеріальної симетрії (
- головний момент сил інерції відносно вісі, що проходить через центр тяжіння С твердого тіла перпендикулярного до площини його матеріальної симетрії ( ),
),  − можливе переміщення центру тяжіння С твердого тіла,
− можливе переміщення центру тяжіння С твердого тіла, 



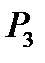 P3
P3

 вантажу А та
вантажу А та  вантажу В по похилій площині.
вантажу В по похилій площині. - вниз, паралельно похилої площини, а
- вниз, паралельно похилої площини, а  - вгору, паралельно похилій площині:
- вгору, паралельно похилій площині:

 , знак якого протилежний до знаку проекції кутового прискорення
, знак якого протилежний до знаку проекції кутового прискорення 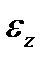 :
: ;
; ,
, ,
, .
. дорівнює нулю, оскільки центр тяжіння блоку розташований на вісі обертання.
дорівнює нулю, оскільки центр тяжіння блоку розташований на вісі обертання. по прямій паралельно похилій площині вгору. Тоді в силу нерозтяжності нитки, вантаж В отримає рівне за модулем можливе переміщення напрямлене вздовж похилої площини вниз, а блок С отримає кутове можливе переміщення
по прямій паралельно похилій площині вгору. Тоді в силу нерозтяжності нитки, вантаж В отримає рівне за модулем можливе переміщення напрямлене вздовж похилої площини вниз, а блок С отримає кутове можливе переміщення  .
. ,
, ,
,  ,
, ,
, ,
, ,
, ,
,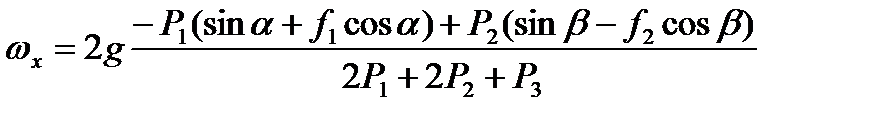 ,
, .
.


