
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В' язі. Класифікація в'язей. Основне завдання динаміки пов'язаних механічних системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У класичній механіці Ньютона розглядаються в основному системи тіл (механічні системи), кожне з яких може займати будь-яке положення в просторі. Такі системи називаються вільними. На практиці часто доводиться стикатися з такими системами, в яких взаємодія тіл між собою або із зовнішніми тілами накладає обмеження на можливі положення тіл та їх швидкості. Такі механічні системи називаються пов'язаними, а обмеження, які накладаються на рух тіл, називають в'язями. Таким чином, у мови, що обмежують свободу переміщень точок механічної системи, називаються в’язями. Наприклад, у техніці при русі окремих ланок машин, місце, зайняте будь-якою її ланкою, вже не може бути зайнятим в ту саму мить часу іншою ланкою і це накладає певне обмеження на свободу руху її ланок. Механічні в’язі розділяються на два основних класи: на в'язі утримуючі і неутримуючі.
Рис. 1 Класифікація в’язей.
В'язь називається утримуючою, якщо обмеження, які вона накладає, виражаються в формі рівності. Звичайно, утримуючі в’язі вводяться умовою, що точки мають знаходитися або на деяких кривих, або на поверхнях у просторі, або не повинні змінюватися відстані між точками і т.п. Механічна в'язь називається неутримуючою, якщо обмеження, які вона накладає на координати точок, виражаються нерівністю Утримуючі механічні в’язі розділяються на кінцеві (геометричні) і диференціальні (кінематичні) в залежності від того, являється рівність, виражаюча їх, кінцевим співвідношенням або диференціальним рівнянням. У тих випадках, коли в’язі накладаються не тільки на координати, але й на швидкості, і тим самим приводять до диференціальних рівнянь, можливі два варіанти в залежності від того, чи можна проінтегрувати ці рівняння чи ні. Якщо диференціальні рівняння в’язі можна проінтегрувати, тоді їх можна записати у вигляді кінцевих співвідношень. Але ці кінцеві співвідношення містять також і довільні постійні, які натуральним шляхом вводяться при інтегруванні диференціальних рівнянь. В тих випадках, коли диференціальне рівняння механічної в’язі не може бути проінтегроване, необхідно враховувати рівняння в’язі в вихідній формі диференціального рівняння. В зв’язку з цим механічні диференціальні в’язі підрозділяються на диференціальні в’язі, що інтегруються і ті, що не інтегруються. Кінцеві в’язі і диференціальні інтегровані складають клас голономних механічних в’язей, а диференціальні неінтегровані в'язі − клас неголономних в’язей. Голономні в'язі − це в'язі, рівняння яких є функцією лише координат точок і можливого часу
Неголономні в'язі - це в'язі, рівняння яких, крім часу і координат точок, містить і їх похідні, тобто
Відповідно системи, що містять тільки кінцеві або диференціальні інтегровані в’язі, відносяться до класу голономних механічних систем, а системи, що містять диференціальні неінтегровані в’язі − до класу неголономних механічних систем. Займатися неголономними в’язями надалі не будемо і тому опускаємо їх класифікацію. Голономні в’язі можуть бути стаціонарними та нестаціонарними, утримуючими та неутримуючими, ідеальними та реальними. Стаціонарні або склерономні в'язі - це в'язі, рівняння яких не містить час. В тих випадках, коли час явно до рівнянь не входить в'язь буде нестаціонарною, або реономною. Звичайно, стаціонарні в’язі мають місце в тих випадках, коли поверхні, або криві, на яких мають знаходитися матеріальні точки, або відстані між цими точками не змінюються з часом. Навпаки, в тих випадках, коли матеріальні точки мають знаходитися на кривих або поверхнях, які самі змінюються з часом, в’язі будуть реономні. Утримуючі в'язі задаються у вигляді рівності. Якщо рівняння в'язі має вигляд нерівності, то в'язь – неутримуюча. Якщо на систему накладено В'язь називається ідеальною, якщо сила реакції перпендикулярна до поверхні зіткнення. Якщо сила реакції не перпендикулярна поверхні в точці зіткнення, то в'язь називається реальною. В цьому випадку її розкладають на нормальну та тангенціальну складові. Тангенціальну складову називають силою тертя. Її виражають через нормальну складову і коефіцієнт тертя
і включають в число діючих (активних) сил. Сили реакції в'язей називають пасивними. На практиці в більшості випадків доводиться зустрічатися з голономними в'язями, які задаються аналітично рівнянями (1.1) і реалізуються у вигляді шарнірів, стержнів, ниток, осей, площин, валів, опор і так далі. Тому надалі розглядатимемо системи лише з такими в'язями. Отже, є механічна система, на яку діють задані сили і рух її обмежено голономними в'язями. Вимагається знайти рівняння руху такої системи і реакції в'язей. Це і є основною задачею пов'язаних систем. Для її розв'язання можна використати систему
де k - кількість в'язей.
Відмітимо, що використання лише системи (1.4) не може бути достатнім для розв'язання основної задачі динаміки пов'язаних систем, оскільки число невідомих в (1.4) є рівним
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.151.211 (0.012 с.) |

 Такі механічні в’язі мають місце звичайно в тих випадках, коли заперечується перебування точки у деякій частині простору. Далі будуть розглядатися тільки утримуючі в’язі і тому загальна класифікація неутримуючих в’язей не приводиться.
Такі механічні в’язі мають місце звичайно в тих випадках, коли заперечується перебування точки у деякій частині простору. Далі будуть розглядатися тільки утримуючі в’язі і тому загальна класифікація неутримуючих в’язей не приводиться. (1.1)
(1.1)
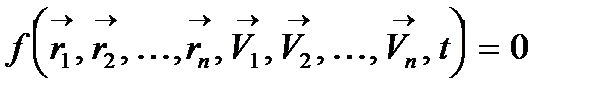 (1.2)
(1.2) утримуючих в'язей, то це призводить до зменшення членів степенів вільності на
утримуючих в'язей, то це призводить до зменшення членів степенів вільності на  ) – 2 степені вільності. Точка, що рухається по прямій (рівняння в'язі
) – 2 степені вільності. Точка, що рухається по прямій (рівняння в'язі  ), має одну степінь вільності. Таким чином, система
), має одну степінь вільності. Таким чином, система  точок, на яку накладено
точок, на яку накладено  степенів вільності.
степенів вільності. (1.3)
(1.3) , (1.4)
, (1.4)
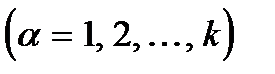 ,
, ,
, .
. (
(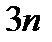 координат та
координат та  ), а рівнянь в (1.4) лише
), а рівнянь в (1.4) лише  . Причому в загальному випадку
. Причому в загальному випадку  .Однак у разі голономних в'язей, завдяки деяким їх властивостям цю задачу можна розв’язати з використанням рівнянь Лагранжа, які надалі будуть одержані. Та спочатку розглянемо деякі поняття, на які в подальшому будемо спиратися.
.Однак у разі голономних в'язей, завдяки деяким їх властивостям цю задачу можна розв’язати з використанням рівнянь Лагранжа, які надалі будуть одержані. Та спочатку розглянемо деякі поняття, на які в подальшому будемо спиратися.


