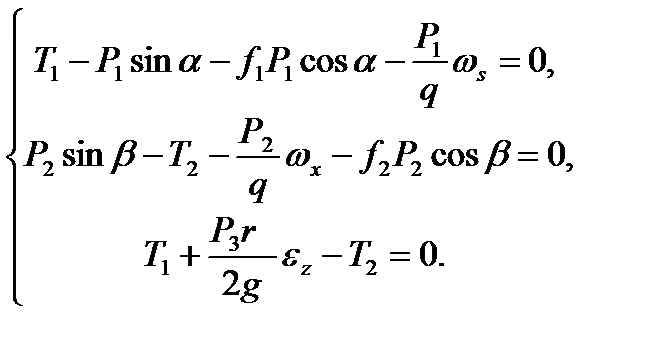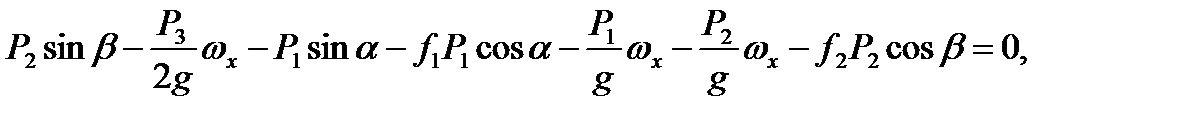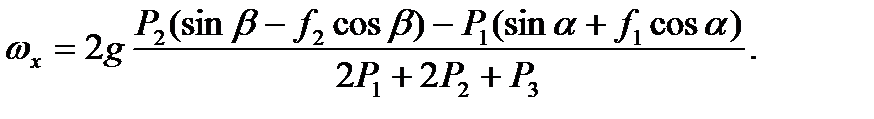Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методом кінетостатики називається формальний прийом, що надає можливості записати рівняння руху у вигляді рівнянь рівноваги.Содержание книги
Поиск на нашем сайте
Застосовуючи цей метод до рухомої матеріальної точки, слід записати умови її "рівноваги" під дією заданих сил, сил реакцій зв'язків, а також фіктивних сил інерції:
де
Методом кінетостатики можна користуватися при розв'язуванні прямих задач динаміки невільної системи матеріальних точок, тобто при розв'язанні задач, в яких по заданому руху визначаються невідомі сили. Проте усі ці задачі при такому ж рівні складності в розрахунках можуть бути розв'язанні звичайним шляхом – за допомогою застосування основного рівняння динаміки до кожної з матеріальних точок системи, тобто
При розв'язуванні обернених задач, в яких по заданих силах визначається рух, застосування методу кінетостатики є абсолютно недоцільним, оскільки в ході розв'язання доводиться інтегрувати систему диференціальних рівнянь руху. Методами кінетостатики можна користуватися у випадках, коли до числа заданих і невідомих величин входять маси матеріальних точок, моменти інерції твердих тіл, швидкості і прискорення точок, кутові швидкості і кутові прискорення твердих тіл, сили і моменти сил.
m B> m A Ð b > Ð a рис.15
Система складається з трьох мас: вантажу А, вантажу В та блоку С (рис.15). Застосовуючи принцип звільнення від в'язей, розглянемо кожну масу окремо. а) Вантаж А:
рис.16
Вантаж А підіймається прискорено вгору по похилій площині, розташованій під кутом a до горизонту, при цьому він рухається поступально з шуканим прискоренням w (рис.16). 1. Вісь q спрямуємо паралельно похилій площині. 2. До вантажу прикладена одна задана сила 3. Сила тертя ковзання Fт.с1
4. Прискорення вантажу А напрямлено уздовж похилої площини вгору. Тому рівнодійна сил інерції j 1 вантажу А спрямована паралельно лінії похилої площини вниз.
Проекція 5. Складємо рівняння "рівноваги" для вантажу А.
б) Вантаж В: Вантаж В переміщуючись по похилій площині, рухається поступально з тим же прискоренням w (внаслідок нерозтяжності нитки) (рис.17).
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAAYx7K8IA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPT2sCMRTE74V+h/CE3mrWLS6yNYoUBE8F/+D5kTw3 azcvyyZq+u2NIHgcZuY3zHyZXCeuNITWs4LJuABBrL1puVFw2K8/ZyBCRDbYeSYF/xRguXh/m2Nt /I23dN3FRmQIhxoV2Bj7WsqgLTkMY98TZ+/kB4cxy6GRZsBbhrtOlkVRSYct5wWLPf1Y0n+7i1Pw dbrsD5tJqs7HqT2nKPVvudZKfYzS6htEpBRf4Wd7YxRUZQWPM/kIyMUdAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQABjHsrwgAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA "/>
рис.17
1. Вісь х, паралельно похилій площині, спрямуємо вниз. 2. На вантаж діє задана сила Р 2, тобто нормальна сила реакції поверхні R та сила реакції нитки Т 2. 3. До вантажу прикладена сила тертя ковзання Fт.с2. Fт.с2=f2N=f2P2 cos b. 4. Прискорення вантажу В напрямлено уздовж похилої площини вниз. Тому рівнодійна сил інерції j2 спрямована паралельно лінії похилої площини вгору:
проекція на вісь х:
5. Складаємо рівняння "рівноваги" для вантажу В.
в) Блок С:
 

рис.18
1. Скеруємо вісь Z уздовж осі обертання блоку С (рис.18). 2. До блоку прикладені: одна задана сила Р3,, сила реакції лівої гілки нитки Т 1, та правої Т 2, складові сили реакцій нерухомої вісі R 1 та R 2. 3. Сил тертя немає оскільки тертям між ниткою та блоком нехтуємо (за умовою задачі). 4. Сили інерції блоку призводять до пари з моментом
5. Складаємо рівняння "рівноваги" для блоку С:
На підставі принципу рівності дії та протидії
тобто за модулем
Проекція точки дотику нитки, яка лежить на ободі блоку рівна
6. Складемо систему рівнянь "рівноваги"
На основі розв’язку даної задачі можна запропонувати такий алгоритм розв’язання інших типових задач з використанням методу кінетостатики: 1. Вибрати систему координат. 2. Зобразити задані сили, що прикладені до кожної з матеріальних точок. 3. Застосувавши принцип звільнення від в'язей, зобразити сили реакцій в'язей, накладених на кожну матеріальну точку системи. 4. Додати до заданих сил і сил реакцій в'язей фіктивні сили інерції матеріальних точок системи. 5. Скласти рівняння "рівноваги" для кожної з матеріальних точок системи. 6. Розв’язавши складену систему рівнянь, визначити шукані величини.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 ,
, - рівнодійна заданих сил, прикладених до матеріальної точки,
- рівнодійна заданих сил, прикладених до матеріальної точки, - рівнодійна сил реакцій зв'язків, накладених на матеріальну точку,
- рівнодійна сил реакцій зв'язків, накладених на матеріальну точку, - сила інерції матеріальної точки, що рівна за моделем добутку маси на модуль її прискорення і за напрямом протилежна прискоренню:
- сила інерції матеріальної точки, що рівна за моделем добутку маси на модуль її прискорення і за напрямом протилежна прискоренню:  .
. .
. , що задається, та сила реакції нитки Т 1, нормальна сила реакції R похилої площини.
, що задається, та сила реакції нитки Т 1, нормальна сила реакції R похилої площини. .
. .
.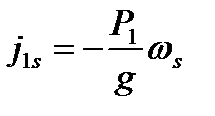 .
.
 .
. ;
;
 ,
, .
. , що обернена за знаком проекції кутового прискорення ez.
, що обернена за знаком проекції кутового прискорення ez. ;
; 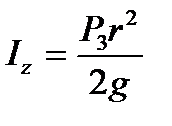 де r - радіус блоку
де r - радіус блоку .
. .
.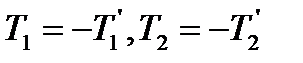 ,
, ,
, .
. .
.