
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Використання принципу можливих переміщень для розв’язання задачСодержание книги
Поиск на нашем сайте
Варіацією функції При переході від функції
Можливим назвається змінна точки цього положення системи, що допускається зв'язями, накладеними на цю точку. Ідеальними називаються в'язі, сума робіт сил реакцій яких на будь-яких можливих переміщеннях точок системи дорівнює нулю, тобто
Принцип можливих переміщень: для рівноваги системи матеріальних точок, що підпорядкована ідеальним стаціонарним в'язям, необхідно і достатньо, щоб сума робіт сил, що задаються на будь-яких можливих переміщеннях точок системи дорівнювали нулю:
Перевагою принципу можливих переміщень є відсутність в його формулюванні сил реакцій ідеальних в'язей. З його допомогою можна досить просто розвязувати задачі про рівновагу твердого тіла і систем твердих тіл, а також визначати залежність між величинами заданих сил. Якщо не усі в'язі, накладені на систему, є ідеальними, то до сил, що задаються, слід додавати сили тертя і прирівнювати до нуля суму робіт не лише заданих сил, але і можливих сил тертя, на будь-яких можливих переміщеннях точок системи. Складені рівняння визначають залежність між заданими силами і силами тертя. Якщо вимагається визначити яку-небудь силу реакцій ідеальної в'язі, для якої Приклад розв’язання задачі.
рис.19
1. До системи прикладені задані сили: 2. Похила площина не є ідеальною в'яззю, тому сили тертя ковзання визначаються як
3. Додамо сили інерції матеріальних точок системи. Нехай вантаж В опускається з шуканим прискоренням w. До вантажів А та В прикладена рівнодійна сил інерції, спрямуємо їх протилежно прискоренням відповідних вантажів
До блоку С прикладемо головний момент сил інерції
Головний вектор сил інерції блоку дорівнює нулю, оскільки центр розташовано на вісі обертання. 4. Надамо вантажу В можливого переміщення Залежність між лінійним та кутовим переміщеннями:
5. Знайдемо суму робіт усіх сил.
Тоді шукане прискорення:
Спираючись на розвязання цієї задачі можна скласти наступний алгоритм: 1. Зобразити задані сили. 2. За наявності неідеальних в'язей додати відповідні сили реакцій в'язей. 3. У разі потреби визначити силу реакції в'язей, подумки відкинути відповідну в'язь та замінити її шуканою силою реакції в'язі (якщо а) У разі системи з одним степенем вільності: 4. Надати можливого переміщення одній з точок системи та виразити можливі переміщення точок прикладання сил залежно від заданого можливого переміщення; 5. Знайти суму робіт усіх сил, вказаних в пунктах 1, 2, 3 на відповідних можливих переміщеннях їх точок прикладання, та прирівняти цю суму до нуля. 6. Розв’язавши складене рівняння рівноваги, визначити шукану величину; б) У разі системи з декількома степенями вільності: 5. Вибрати незалежні можливі переміщення точок системи таким чином, щоб їх число було рівним числу степенів вільності цієї системи. 6. Надати можливого переміщення, що відповідає одному із степенів вільності системи, вважаючи при цьому рівними нулю можливі переміщення, що відповідають залишившимся системам вільності. Виразити можливі переміщення точок прикладання сил залежно від заданого можливого переміщення. 7. Знайти суму робіт усіх сил, вказаних в пунктах 1, 2, 3 на відповідних можливих переміщеннях їх точок прикладення, прирівняти цю суму до нуля. 8. Послідовно повторюючи викладки пунктів 5 та 6 для кожного з незалежних можливих переміщень, скласти систему рівнянь рівноваги таким чином, щоб їх число було рівним числу степенів вільності цієї системи, тобто числу степенів вільності системи. 9. Розв’язавши| систему відповідних рівнянь рівноваги визначити шукану величину.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.36 (0.008 с.) |

 називається приріст функції, обумовлений зміною виду функції, при фіксованому значенні аргументу.
називається приріст функції, обумовлений зміною виду функції, при фіксованому значенні аргументу. до функції
до функції 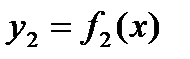 варіацію функції
варіацію функції  можна знайти як:
можна знайти як:

 - сила реакції в'язі.
- сила реакції в'язі. - можливе переміщення k -ої матеріальної точки системи.
- можливе переміщення k -ої матеріальної точки системи. .
. , то слід, застосовуючи принцип звільненої від в'язей, відкинути відповідну в'язь і замінити її шуканою силою реакції. При складанні рівняння рівноваги потрібно до сил, що задаються, додати цю силу реакції в'язі. Такий метод розвязання задач в рівновазі систем твердих тіл є надзвичайно ефективним, оскільки шукана сила реакції в'язі безпосередньо визначається зі складеного рівняння
, то слід, застосовуючи принцип звільненої від в'язей, відкинути відповідну в'язь і замінити її шуканою силою реакції. При складанні рівняння рівноваги потрібно до сил, що задаються, додати цю силу реакції в'язі. Такий метод розвязання задач в рівновазі систем твердих тіл є надзвичайно ефективним, оскільки шукана сила реакції в'язі безпосередньо визначається зі складеного рівняння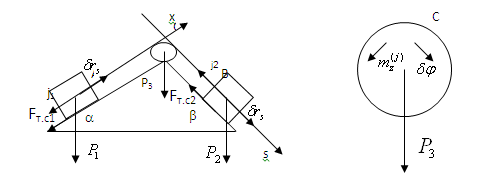
 - вага вантажу А,
- вага вантажу А,  - вага вантажу В,
- вага вантажу В,  - вага вантажу С (рис.19)
- вага вантажу С (рис.19) ;
;
 ,
, .
. , знак якого протилежний до знаку проекції умовного прискорення
, знак якого протилежний до знаку проекції умовного прискорення  :
: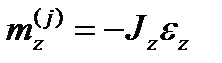 ;
;
 ,
, .
. . Тоді внаслідок нерозтяжності нитки, вантаж А отримає рівне за модулем можливе переміщення, спрямоване уздовж похилої площини вгору, а блок С отримає кутове можливе переміщення
. Тоді внаслідок нерозтяжності нитки, вантаж А отримає рівне за модулем можливе переміщення, спрямоване уздовж похилої площини вгору, а блок С отримає кутове можливе переміщення  .
. .
. ,
, ,
,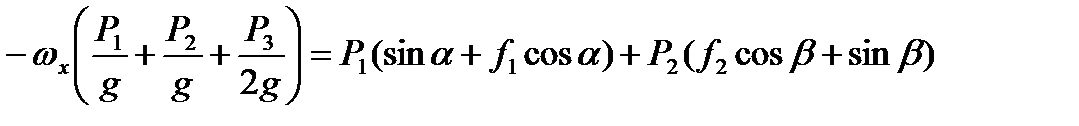 ,
,
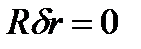 ).
).


