
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Узагальнені координати і узагальнені швидкості та прискоренняСодержание книги
Поиск на нашем сайте
Розв'язння задач динаміки невільних систем має ряд ускладненнь. При зменшенні числа степенів вільності, тобто при спрощенні руху системи, задача з погляду математики не спрощується, а навпаки; збільшується кількість невідомих величин, що підлягають визначенню, і кількість рівнянь що потрібно розв’язати. Крім того, навіть при ідеальних в'язях не вдається відокремити пряму задачу динаміки від оберненої (знаходження невідомих сил – реакцій в'язей). Детальний аналіз цих ускладнень привів до висновку, що для їх усунення суттєвим є вибір сукупності параметрів, які визначають положення системи у просторі. Дотепер положення точок описувалося декартовими координатами. Але існують і інші системи координат, які дозволяють для деяких видів руху системи більш просто описати положення її точок. Наприклад, при русі рідини у круглій трубі зручно використовувати циліндричні координати. При цьому положення частинки рідини М визначається кутом Між декартовими координатами
У деяких випадках, як, наприклад, при розповсюдженні хвиль, застосовують сферичні координати. Положення точки у сферичних координатах визначається відстанню
Між сферичними координатами і координатами Декарта існує залежність
Розглянемо невільну матеріальну точку, що рухається по поверхні. Рівняння поверхні (в’язі)
Точка М має два степеня вільності N = 2. Але для вивчення руху точки М потрібно скласти три рівняння при наявності трьох невідомих величин: дві координати та модуль реакції, напрямленої по нормалі до поверхні. Лагранж показав, що у випадку, коли на тіло накладено геометричні в’язі, можна вибрати систему таких недекартових координат, названих ним узагальненими координатами, котрі дозволяють розділити задачу про рух невільних точок і систем на дві окремі: спочатку визначити закон руху, потім за відомим законом руху визначити реакції в’язей.
Взагалі, узагальненими координатами називається система параметрів, які однозначно визначають положення всіх точок системи у кожен момент часу. Наприклад, положення точки М можуть визначити дві незалежні координати
Узагальнюючи викладене, можна стверджувати, що положення системи, складеної із Якщо положення точок системи визначається N узагальненими координатами, то між ними та декартовими координатами повинен існувати зв’язок. Декартові координати завжди можна однозначно виразити через узагальнені:
Рівняння (3.1) – параметричні рівняння в’язей, накладених на точки системи, із параметрами qj. Дійсно, якщо система невільна, то Виберемо N рівнянь із системи (3.1) і розв`яжемо відносно узагальнених координат
що визначають нестаціонарні в’язі. Введення узагальнених координат автоматично задовольняє тим умовам, що накладають в’язі на рух точок системи. Систему трьох скалярних залежностей (3.1) можна замінити однією векторною залежністю
Час t у рівняннях (3.1) та (3.3) входить у тому випадку, коли в’язь нестаціонарна. В якості прикладу розглянемо кривошипно-шатунний механізм (рис.4). Ведучий ланцюг – кривошип
 L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAOBntxcQA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE7wX/w/KE3uquxQaNboJUhJ5amqrg7ZF9 JsHs25BdTfrvu4VCj8PMfMNs8tG24k69bxxrmM8UCOLSmYYrDYev/dMShA/IBlvHpOGbPOTZ5GGD qXEDf9K9CJWIEPYpaqhD6FIpfVmTRT9zHXH0Lq63GKLsK2l6HCLctvJZqURabDgu1NjRa03ltbhZ Dcf3y/m0UB/Vzr50gxuVZLuSWj9Ox+0aRKAx/If/2m9GQzJfwe+ZeARk9gMAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhADgZ7cXEAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= " filled="f" stroked="f"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAOBntxcQA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE7wX/w/KE3uquxQaNboJUhJ5amqrg7ZF9 JsHs25BdTfrvu4VCj8PMfMNs8tG24k69bxxrmM8UCOLSmYYrDYev/dMShA/IBlvHpOGbPOTZ5GGD qXEDf9K9CJWIEPYpaqhD6FIpfVmTRT9zHXH0Lq63GKLsK2l6HCLctvJZqURabDgu1NjRa03ltbhZ Dcf3y/m0UB/Vzr50gxuVZLuSWj9Ox+0aRKAx/If/2m9GQzJfwe+ZeARk9gMAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhADgZ7cXEAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= " filled="f" stroked="f">
рис.4
рис.5
Кривошип з’єднаний шарнірно в точці Знайдемо вектор швидкості i -тої точки системи
Зауваживши, що
Похідні від узагальнених координат за часом називаються узагальненими швидкостями, а другі похідні за часом від узагальнених координат (або похідні за часом від узагальнених швидкостей) називаються узагальненими прискореннями. Позначаються вони відповідно
Швидкість і -тої точки
Із (3.5) видно, що вектор швидкості – лінійна функція узагальненої швидкості. Знайдемо співвідношення, котре буде використано при виводі рівнянь Лагранжа другого роду – частинну похідну від швидкості
або
Узагальнені сили та їх визначення
Формула (3.7) показує приріст До поняття про узагальнені сили прийдемо, виразивши елементарну роботу
Підставимо значення
Вираз
називається узагальненою силою. Елементарна робота набуває вигляду
Щоб зрозуміти фізичний зміст узагальненої сили, розглянемо елементарну роботу, виконану силою, що діє на одну матеріальну точку

рис.6 рис.7
Для матеріальної точки декартові координати є також узагальненими. Це означає, що
Узагальненою силою називається фізична величина, яка має таку властивость: добуток узагальненої сили та варіації відповідної її узагальненої координати рівний елементарній роботі, що виконують сили на будь-яких можливих переміщеннях точок системи, визначених зміною цієї узагальненої координати. Покажемо, що для визначеного класу в’язей, які називають ідеальними, узагальнені сили залежать лише від активних сил і не залежать від реакції в’язей. Як приклад ідеальної в’язі наведемо ідеально гладку поверхню. У зв’язку з відсутністю сили тертя, реакція такої поверхні
Ідеальною в’яззю можна вважати також жорсткий стержень, що з’єднує точки М1 та М2 (рис.7). Реакції стержня Надамо точкам М1 та М2 можливі переміщення Із рівності
Знаку нерівності тут бути не може, бо точки не можуть здійснювати рухи, при яких вони покидають в’язь. Для ідеальних в’язей узагальнені сили залежать не від їх реакцій, а лише від активних сил. При розгляді реальних в’язей їх можна наближено вважати ідеальними, віднісши сили тертя до активних сил. Існує інший спосіб визначення узагальненої сили. Якщо система рухається в потенціальному силовому полі, тобто вона консервативна, то узагальнена сила виражається через силову функцію U = U (q 1, q 2,…,q N). Елементарну роботу консервативних сил на можливих переміщеннях можна подати у вигляді
Отже, для узагальненої сили дістанемо вираз
Виражаючи силову функцію через потенціальну енергію П, отримаємо
Сформулюємо правило визначення узагальнених сил. Щоб знайти узагальнену силу, потрібно надати варіацію узагальненій координаті; знайти елементарну роботу, що виконується активними силами на можливих переміщеннях точок системи, які відповідають варіації узагальненої координати. Коефіцієнт при варіації узагальненої координати у виразі елементарної роботи дорівнює шуканій узагальненій силі. Принцип, який визначає необхідні та достатні умови рівноваги голономних систем з ідеальними стаціонарними в'язями, встановив Д. Бернуллі в 1717 р.
Раніше ми говорили, що в'язь є ідеальною, якщо сила реакції в'язі перпендикулярна поверхні зіткнення. Оскільки віртуальні переміщення в цьому випадку є дотичними до цієї поверхні, то робота сил реакції на будь-якому віртуальному переміщенні дорівнюватиме нулю. У багатьох випадках в'язі є не поверхнями. Наприклад, кулька, підвішена на нитці (мал. 8). В цьому випадку віртуальне переміщення кульки є дотичними до сфери радіуса
рис.8
Принцип віртуальних переміщень формулюють таким чином: Для рівноваги будь-якої механічної системи з голономними, стаціонарними, утримуючими, ідеальними в'язями необхідно і достатньо, щоб сума віртуальних робіт активних сил на будь-якому віртуальному переміщенні дорівнювала нулю
Доведемо необхідність умови (3.16) для рівноваги системи. Нехай є система
Надамо системі віртуального переміщення, помножимо попередній вираз на віртуальне переміщення та підсумуємо по усіх точках з урахуванням (3.11), отримаємо
Необхідність доведена. Доведемо достатність умови (3.16). Припустимо, що умови (3.16) виконуються, але система все ж таки виходить із стану спокою. При цьому кожна точка рухатиметься у напрямі результуючої сили
Виберемо віртуальні переміщення системи так, щоб вони співпадали з дійсними, тоді
Або з урахуванням (3.11)
що суперечить умові. Розглянемо два приклади. Приклад 1. Рівновага механічної системи з ідеальними голономними в'язями, що перебуває в полі сил тяжіння. Декартові координати точок Згідно (3.16)
або
Використовуючи формулу для радіус-вектора центру мас, маємо
тоді
Тобто така система буде знаходитися у стані спокою лише тоді, коли центр мас матиме найбільше або найменше значення, а в загальному випадку –стаціонарне значення (див. рис.9).
рис. 9 Приклад 2. Розглянемо вільне абсолютно тверде тіло. Його можна розглядати як механічну систему з внутрішніми в'язями, рівняння яких
Оскільки в'язі стаціонарні, то в якості віртуального переміщення
помноживши на
Підставимо цей вираз в принцип віртуальних переміщень
Скористаємось відомою формулою для змішаного добутку
Тоді
Оскільки
тобто тверде тіло буде в рівновазі, якщо сума моментів сил, діючих на нього, дорівнюватиме нулю Тоді умови рівноваги набудуть вигляду
або
тобто
Це може бути Оскільки віртуальні переміщення незалежні, то умовами рівноваги вільного абсолютно твердого тіла будуть:
тобто тіло знаходиться в рівновазі, якщо векторна сума сил дорівнює нулю і якщо векторна сума моментів сил відносно будь-якої точки дорівнюватиме нулю. У виразах (3.17) маються на увазі зовнішні сили, оскільки для внутрішніх сил
та
На закінчення відмітимо, що існують 4 типи положень рівноваги: 1.
рис.10.а Йому відповідає min потенціальної енергії (рис. 10. а). При виведенні системи з положення рівноваги виникає сила спрямована до положення рівноваги.
2. Нестійке рис.10.б Цьому стану рівноваги відповідає max потенціальної енергії. При виведенні тіла зі стану рівноваги (рис. 10. б) виникає сила, що віддаляє тіло від положення рівноваги. Байдуже
рис.10.в
При виведенні тіла з положення рівноваги його потенціальна енергія не змінюється (мал. 10. в). Сідлоподібне
рис. 10.г Рівновага залежить від напряму зрушення.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.134.54 (0.009 с.) |

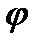 , відстанню
, відстанню  і координатою
і координатою 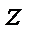 (рис.2);
(рис.2);  , то пряма, паралельна вісі
, то пряма, паралельна вісі 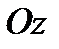 , опише навколо вісі
, опише навколо вісі  і циліндричними
і циліндричними  можна знайти залежність
можна знайти залежність

 . (а)
. (а) і
і 



 . (b)
. (b)
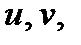 що називаються координатами Гаусса, котрі і будуть узагальненими координатами. Параметричними рівняннями руху будуть
що називаються координатами Гаусса, котрі і будуть узагальненими координатами. Параметричними рівняннями руху будуть ;
;  ;
;  . (c)
. (c) матеріальних точок, яка має N степенів вільності, визначають N узагальнених координат
матеріальних точок, яка має N степенів вільності, визначають N узагальнених координат  . Як видно, число узагальнених координат є рівним числу степенів вільності системи.
. Як видно, число узагальнених координат є рівним числу степенів вільності системи.
 (3.1)
(3.1) .
. . При цьому знайдемо qj як функції декартових координат точок системи xi, yi, zi та часу t. Таким чином отримаємо k = 3n – N рівнянь, що пов’язують декартові координати xi, yi, zi та час t, тобто рівняння вигляду
. При цьому знайдемо qj як функції декартових координат точок системи xi, yi, zi та часу t. Таким чином отримаємо k = 3n – N рівнянь, що пов’язують декартові координати xi, yi, zi та час t, тобто рівняння вигляду
 (3.2)
(3.2)
 (3.3)
(3.3) обертається навколо вісі
обертається навколо вісі  , перпендикулярної до площини розташування механізму.
, перпендикулярної до площини розташування механізму.
 з шатуном
з шатуном 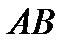 і приводить його до руху. Точка
і приводить його до руху. Точка  (повзун) рухається прямолінійно. Розташування всіх ланцюгів механізму буде відоме у кожний момент часу t, якщо відомий кут повороту кривошипа
(повзун) рухається прямолінійно. Розташування всіх ланцюгів механізму буде відоме у кожний момент часу t, якщо відомий кут повороту кривошипа  , виразивши його через узагальнені координати. із кінематики відомо, що
, виразивши його через узагальнені координати. із кінематики відомо, що (d)
(d) - складна функція часу, отримаємо
- складна функція часу, отримаємо (e)
(e)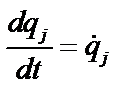 (j = 1,2,…,N).
(j = 1,2,…,N). (j = 1,2,…,N). (3.4)
(j = 1,2,…,N). (3.4) (3.5)
(3.5) по узагальненій швидкості
по узагальненій швидкості
 …,
…, 

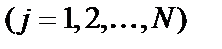 (3.6)
(3.6) (3.7)
(3.7) для випадку, коли узагальнена координата отримує приріст
для випадку, коли узагальнена координата отримує приріст  .
.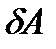 через узагальнені координати. Знайдемо елементарну роботу сил, що діють на точки системи, на можливих переміщеннях, вирахувавши її як скалярний добуток
через узагальнені координати. Знайдемо елементарну роботу сил, що діють на точки системи, на можливих переміщеннях, вирахувавши її як скалярний добуток
 (3.8)
(3.8) (3.9)
(3.9) (3.10)
(3.10)

 виражають досить малі прирости узагальнених координат, тобто мають те ж розуміння, що і
виражають досить малі прирости узагальнених координат, тобто мають те ж розуміння, що і  у (3.10). Коєфіцієнти
у (3.10). Коєфіцієнти  при варіаціях узагальнених координат у виразі (3.10) є проекціями сили. Тому коефіцієнти
при варіаціях узагальнених координат у виразі (3.10) є проекціями сили. Тому коефіцієнти  при варіаціях узагальнених координат назвали узагальненими силами (Qj можуть бути також і моментами сил).
при варіаціях узагальнених координат назвали узагальненими силами (Qj можуть бути також і моментами сил). направлена по нормалі до її елемента (рис.6). Можливі переміщення точки прикладання реакції
направлена по нормалі до її елемента (рис.6). Можливі переміщення точки прикладання реакції  лежать в площині, дотичній до опорної поверхні. Робота реакції на можливе переміщення рівна нулю:
лежать в площині, дотичній до опорної поверхні. Робота реакції на можливе переміщення рівна нулю: (3.11)
(3.11) та
та  напрямлені вздовж нього в протилежні напрямки і рівні між собою за величиною.
напрямлені вздовж нього в протилежні напрямки і рівні між собою за величиною. та
та  , знайдемо роботу реакцій
, знайдемо роботу реакцій  та
та  на цих переміщеннях за формулою (3.2), що виражає теорему про роботу сил, які діють на абсолютно тверде тіло.
на цих переміщеннях за формулою (3.2), що виражає теорему про роботу сил, які діють на абсолютно тверде тіло. (3.12)
(3.12) (3.13)
(3.13) (3.14)
(3.14) (3.15)
(3.15) , а сила реакції в'язі напрямлена вздовж
, а сила реакції в'язі напрямлена вздовж 
 . (3.16)
. (3.16) точок, на яку накладені стаціонарні, утримуючі, ідеальні голономні в'язі і в деякий момент часу вона перебуває в рівновазі, тобто усі її точки покояться. Це означає, що сума усіх сил діючих на
точок, на яку накладені стаціонарні, утримуючі, ідеальні голономні в'язі і в деякий момент часу вона перебуває в рівновазі, тобто усі її точки покояться. Це означає, що сума усіх сил діючих на  -ту точку, дорівнює нулю.
-ту точку, дорівнює нулю.

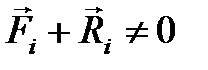
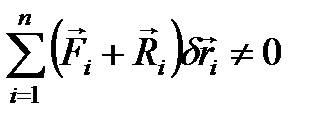
 ,
,

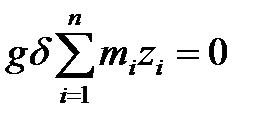 .
. ,
,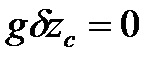 ,
,

 .
. можна узяти дійсне
можна узяти дійсне  . Швидкість
. Швидкість  -тої точки твердого тіла визначається формулою
-тої точки твердого тіла визначається формулою ,
, , отримаємо
, отримаємо .
.
 .
. .
. і
і  незалежні варіації, то остання умова рівноваги твердого тіла набуде вигляду:
незалежні варіації, то остання умова рівноваги твердого тіла набуде вигляду:
 ,
,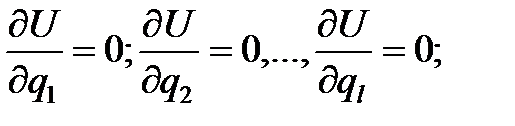
 ,
, .
. або
або  , або стаціонарне значення.
, або стаціонарне значення. ,
, , (3.17)
, (3.17)
 .
.
 L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAmvF43cAA AADdAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdD/gP4QruxsTiDFqNIjMIrkbGF7i7NNe2 2NyUJtr692YhuDyc93zZ2UrcqfGlYw2joQJBnDlTcq7hsF9/TkD4gGywckwaHuRhueh9zDE1ruV/ uu9CLmII+xQ1FCHUqZQ+K8iiH7qaOHIX11gMETa5NA22MdxWMlHqW1osOTYUWNNPQdl1d7Majn+X 82mstvmv/apb1ynJdiq1HvS71QxEoC68xS/3xmhIEhXnxjfxCcjFEwAA//8DAFBLAQItABQABgAI AAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsB Ai0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxzUEsB Ai0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXhtbC54 bWxQSwECLQAUAAYACAAAACEAmvF43cAAAADdAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA9QAAAIUDAAAAAA== " filled="f" stroked="f">
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAmvF43cAA AADdAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdD/gP4QruxsTiDFqNIjMIrkbGF7i7NNe2 2NyUJtr692YhuDyc93zZ2UrcqfGlYw2joQJBnDlTcq7hsF9/TkD4gGywckwaHuRhueh9zDE1ruV/ uu9CLmII+xQ1FCHUqZQ+K8iiH7qaOHIX11gMETa5NA22MdxWMlHqW1osOTYUWNNPQdl1d7Majn+X 82mstvmv/apb1ynJdiq1HvS71QxEoC68xS/3xmhIEhXnxjfxCcjFEwAA//8DAFBLAQItABQABgAI AAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsB Ai0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxzUEsB Ai0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXhtbC54 bWxQSwECLQAUAAYACAAAACEAmvF43cAAAADdAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA9QAAAIUDAAAAAA== " filled="f" stroked="f"> 




