
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ ІІ. Використання основних положень механіки Лагранжа для розв’язання задач динамікиСодержание книги
Поиск на нашем сайте
При розв'язанні задач динаміки часто виникають труднощі, пов'язані з вибором відповідних теорій і рівнянь. Для набуття навичок розв'язання задач треба спробувати різні методи розв'язання. Задачі динаміки можна розбити на 3 групи: ü задача динаміки матеріальної точки; ü задачі динаміки системи матеріальних точок; ü задачі динаміки твердого тіла. При розв'язанні задач динаміки, треба звернути увагу на те що: 1. Ефективність розв'язання задачі динаміки значною мірою залежить від вдалого вибору системи координат. 2. Основними і в той же час найбільш важкими є зворотні задачі, в яких по заданих силах визначається рух. При цьому доводиться інтегрувати систему диференціальних рівнянь руху. Ці задачі не завжди можна розв'язати в квадратурі. Іноді доводиться застосовувати наближені методи інтегрування. 3. Зручність застосування загальних теорем динаміки полягає в можливості обійти інтегрування диференціальних рівнянь руху системи. Проте ці загальні теореми можуть застосовуватися тільки в деяких випадках. Зручно і те, що у формулювання загальних теорем динаміки не входять внутрішні сили, визначення яких зазвичай пов'язано зі значними труднощами. 4. Найбільш загальним прийомом складання диференціальних рівнянь руху є застосування рівнянь Лагранжа або загального рівняння динаміки Замість штучного поєднання деяких загальних теорем і рівнянь динаміки, вибір яких надає значних складнощів, вказані методи швидко призводять до складання диференціальних рівнянь руху. Вдалий вибір узагальнених коефіцієнтів забезпечує швидкість розв'язання задачі. 5. Застосовуючи загальні теореми динаміки, диференціальне рівняння обертання твердого тіла навколо нерухомої вісі, диференціальні рівняння плоского руху твердого тіла, динамічні рівняння Ейлера, рівняння Лагранжа, часто в число даних сил зазвичай включають й сили інерції. Силами інерції користуються тільки у разі застосування: а) методу кінетостатики; б) загального рівняння динаміки; в) дослідження відносного руху матеріальної точки або системи матеріальних точок. 6. При розв'язанні задач за допомогою загальних теорем динаміки, а також при застосуванні диференціального рівняння обертання твердого тіла навколо нерухомої вісі, диференціальних рівнянь плоского руху твердого тіла і динамічних рівнянь Ейлера сили діляться на зовнішні і внутрішні. При розв'язанні задач за допомогою рівнянь Лагранжа, загального рівняння динаміки і методу кінетостатики сили діляться на задані і сили реакцій в'язей. Розглянемо розв'язання задач за допомогою вказаних вище методів розглянуто на прикладі наступної задачі:
Вантажі А та В з’єднані тонкою нерозтяжною ниткою, перекинутою через блок С (рис.14). При опусканні вантажу В масою m 2 вниз по похилій площині, розташованій під кутом b до горизонту, блок С масою m 3 обертається навколо своєї нерухомої вісі. При цьому вантаж А масою m 1 піднімається вгору по похилій площині, що розташована під кутом a до горизонту. Визначити прискорення вантажів. Коефіцієнт тертя ковзання вантажу А об похилу площину f 1, вантажу В – f 2. Блок вважати однорідним круглим диском. Масою нитки знехтувати.
     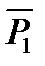 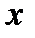  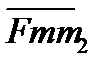   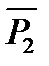      Перед розглядом аналітичних методів розв'язання задач розглянемо розв'язання цієї задачі, використовуючи закон Ньютона. Перед розглядом аналітичних методів розв'язання задач розглянемо розв'язання цієї задачі, використовуючи закон Ньютона.
Надалі, провівши аналіз розв'язання задачі тим або іншим методом, можна порівняти метод аналітичної механіки з класичним методом.
Рис. 14 1. Запишемо рівняння руху для вантажу А:
Виберемо вісі координат x та y і запишемо це рівняння в проекціях на ці вісі:
Як відомо
2. Запишемо рівняння руху для вантажу B:
Виберемо вісі координат х ' і у ' і виразимо це рівняння в проекціях на ці вісі:
Аналогічно п. 1 отримаємо
3. Запишемо рівняння руху для тіла С. Сили інерції блоку призводять до пари з моментом
де
Виразимо рівняння руху блоку в проекції на вісь
З принципу рівності дії та протидії
Проекція точки нитки, що знаходиться на ободі блоку дорівнює:
4. Запишемо систему рівнянь, що описує рух матеріальної системи.
Розв’язуючи цю систему рівнянь, отримаємо наступний результат:
Складемо алгоритм розв’язання типових задач методом механіки Ньютона: 1. Вибрати систему координат. 2. Зобразити задані сили, що прикладені до кожної з матеріальних точок. 3. Зобразити сили реакцій в'язей. 4. Скласти основне рівняння динаміки у векторній формі: 5. Розв’язуючи одержану систему рівнянь, знайти шукану величину. 6. Якщо число невідомих більше числа рівнянь в системі, то необхідні рівняння записуються на основі формул кінематики або закону збереження енергії.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.219 (0.009 с.) |

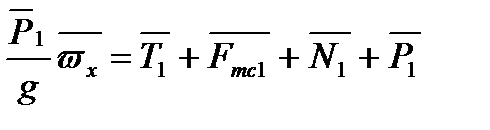
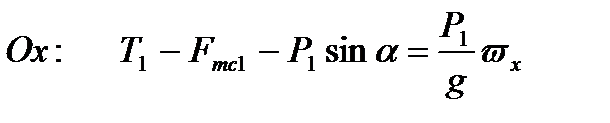 ,
,
 , тоді
, тоді . (2.1)
. (2.1) .
. ,
, .
.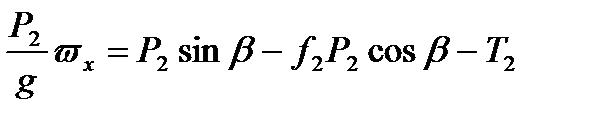 (2.2)
(2.2) , що є оберненим за знаком проекції кутового прискорення
, що є оберненим за знаком проекції кутового прискорення 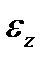 .
.
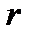 - радіус блоку
- радіус блоку .
. :
: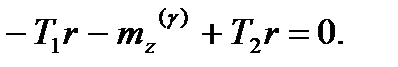
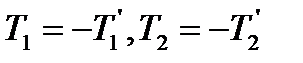 , т. т. за модулем
, т. т. за модулем 
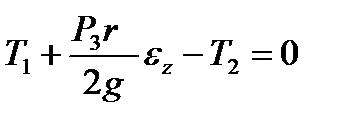

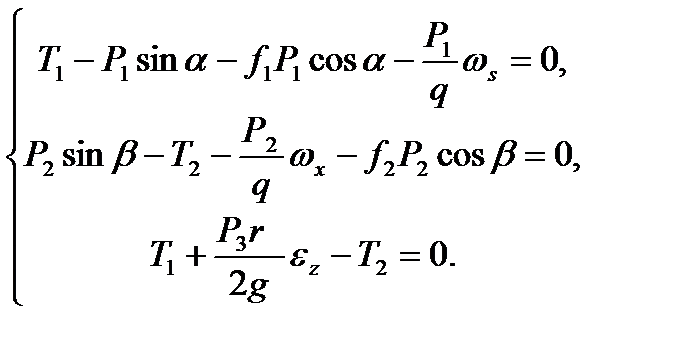

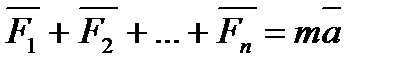 та в проекціях на вибрані вісі:
та в проекціях на вибрані вісі: 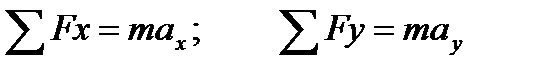 .
.


