
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рух матеріальної точки під дією сили тяжіння.Содержание книги
Поиск на нашем сайте
Рух матеріальної точки під дією сили тяжіння.
Дослідимо рух матеріальної точки маси Ми знаємо з механіки закон Ньютона З механічного змісту другої похідної випливає, що прискорення дорівнює
Процеси першого порядку.
Багато хімічних реакцій та фізичних процесів характеризуються тим, що швидкість зміни однієї змінної величини відносно другої пропорційно значенню цієї змінної у першому степені. Такі процеси називаються процесами першого порядку. Вони визначаються рівнянням
Основні означення. Означення 1. Диференціальним рівнянням називається рівняння, яке зв`язує шукану функцію, її похідні та аргумент, тобто воно має вигляд
Якщо шукана функція Означення 2. Найвищий порядок похідної. що входить у диференціальне рівняння, називається порядком диференціального рівняння (наприклад, Означення 3. Розв`язком або інтегралом диференціального рівняння називається будь-яка функція Приклад. Функції
Функції
Рівняння з відокремлюваними змінними. Означення. Диференціальним рівнянням з відокремлюваними змінними називається рівняння вигляду
Порівняно із загальним виглядом рівняння першого порядку
Якщо
Зауваження. Диференціальне рівняння з відокремлюваними змінними можна подати у вигляді
Приклад. Знайти частинний розв`язок рівняння
Зробимо перетворення
і відокремимо змінні (поділивши обидві частини рівняння на
зінтегрувавши рівняння, одержимо
або
Визначимо з початкових умов довільну сталу:
а потім, підставивши знайдене значення довільної сталої у загальний інтеграл, знайдемо шуканий частинний інтеграл
Рівняння Бернуллі.
Означення. Диференціальне рівняння вигляду
де Зведемо рівняння Бернуллі до лінійного. Поділимо обидві частини рівняння (7.1) на
Зробимо заміну шуканої функції
Знаходимо загальний розв`язок останнього рівняння і підставимо замість Зауваження. Тому що рівняння Бернуллі зводиться до лінійного рівняння, його розв`язок можна шукати у вигляді
Приклад. Розв`язати рівняння Шукаємо розв`язок рівняння у вигляді
Для знаходження функції
звідки Підставивши знайдене значення
Зінтегрувавши, знаходимо Таким чином, загальний розв`язок рівняння
Знайдемо частинний розв`язок рівняння, який задовольняє заданим початковим умовам:
Підставимо знайдене значення довільної сталої у загальний розв`язок і добудемо шуканий частинний розв`язок:
Питання для самоперевірки.
1. Яке рівняння називається диференціальним? 2. Що називають порядком диференціального рівняння? 3. Який вигляд має диференціальне рівняння першого порядку, яке розв`язане відносно похідної? 4. Що називають розв`язком диференціального рівняння? 5. Що називають інтегральною кривою диференціального рівняння 6. Сформулювати задачу Коші для диференціального рівняння 7. Що називається загальним розв`язком диференціального рівняння 8. Як із загального розв`язку диференціального рівняння добути частинний розв`язок? 9. Яке диференціальне рівняння називається рівнянням з відокремлюваними змінними? 10. Дати означення однорідної функції і однорідного диференціального рівняння першого порядку. 11. Як розв`язати однорідне рівняння першого порядку? 12. Дати означення лінійного рівняння першого порядку. Як розв`язати таке рівняння? 13. Який вигляд має рівняння Бернуллі? 14. Як розв`язати рівняння Бернуллі? 15. Дати означення рівняння у повних диференціалах. Рівняння вищих порядків.
У загальному випадку рівняння
Задача, яка полягає у знаходженні розв`язку (9.1), який задовольняє початкові умови
називається задачею Коші. Розв`язок задачі Коші дає теорема. Теорема Коші. Якщо в рівнянні (9.1) функція Загальним розв`язком (інтегралом) називається функція яка задовольняє умови: 1) при довільних сталих 2) при довільних умовах (9.2) існують такі сталі Частинний розв`язок (інтеграл) дістаємо із загального при
Питання для самоперевірки. 1. Який загальний вигляд диференціального рівняння 2. Що називають розв`язком диференціального рівняння? 3. Сформулювати задачу Коші для диференціального рівняння 4. Дати означення загального розв`язку диференціального рівняння 5. Якими методами можна знизити порядок диференціального рів? 6. Як добути характеристичне рівняння однорідного диференціального рівняння зі сталими коефіцієнтами? 7. Як добути загальний розв`язок однорідного рівняння у випадку: а) корені характеристичного рівняння дійсні і різні; б) дійсні і рівні; в) комплексні спряжені? 8. Як добути загальний розв`язок лінійного неоднорідного рівняння?
Рух матеріальної точки під дією сили тяжіння.
Дослідимо рух матеріальної точки маси Ми знаємо з механіки закон Ньютона З механічного змісту другої похідної випливає, що прискорення дорівнює
Процеси першого порядку.
Багато хімічних реакцій та фізичних процесів характеризуються тим, що швидкість зміни однієї змінної величини відносно другої пропорційно значенню цієї змінної у першому степені. Такі процеси називаються процесами першого порядку. Вони визначаються рівнянням
Основні означення. Означення 1. Диференціальним рівнянням називається рівняння, яке зв`язує шукану функцію, її похідні та аргумент, тобто воно має вигляд
Якщо шукана функція Означення 2. Найвищий порядок похідної. що входить у диференціальне рівняння, називається порядком диференціального рівняння (наприклад, Означення 3. Розв`язком або інтегралом диференціального рівняння називається будь-яка функція Приклад. Функції
Функції
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.134.195 (0.009 с.) |

 по вертикальній прямій під дією сили земного тяжіння. Нехай вісь
по вертикальній прямій під дією сили земного тяжіння. Нехай вісь  - пряма по, якій рухається матеріальна точка, початок координат візьмемо на поверхні землі, а додатній напрям будемо відраховувати догори. Щоб знати рух, тобто положення точки у будь-який момент часу
- пряма по, якій рухається матеріальна точка, початок координат візьмемо на поверхні землі, а додатній напрям будемо відраховувати догори. Щоб знати рух, тобто положення точки у будь-який момент часу  після початку руху (яке відповідає значенню
після початку руху (яке відповідає значенню  ), потрібно знати значення єдиної координати цієї точки
), потрібно знати значення єдиної координати цієї точки  як функції t. Таким чином, незалежною змінною є
як функції t. Таким чином, незалежною змінною є  , а шуканою функцією
, а шуканою функцією  , де
, де  - відповідно маса та прискорення матеріальної точки;
- відповідно маса та прискорення матеріальної точки; 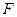 - сила, яка діє на точку.
- сила, яка діє на точку. , з іншого боку ми знаємо, що прискорення сили земного тяжіння у кожній точці поверхні і поблизу Землі є сталою, яка дорівнює
, з іншого боку ми знаємо, що прискорення сили земного тяжіння у кожній точці поверхні і поблизу Землі є сталою, яка дорівнює  , а сила тяжіння дорівнює
, а сила тяжіння дорівнює  . Тому що сила тяжіння напрямлена униз у нашій системі координат їй належить дати знак „- “. Порівнюючи обидва знайдені вирази, одержуємо рівняння руху
. Тому що сила тяжіння напрямлена униз у нашій системі координат їй належить дати знак „- “. Порівнюючи обидва знайдені вирази, одержуємо рівняння руху  або
або 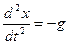 .
. . У випадку хімічної реакції маємо
. У випадку хімічної реакції маємо  - стала величина (константа швидкості реакції),
- стала величина (константа швидкості реакції),  або
або 
 є функцією однієї незалежної змінної, то диференціальне рівняння називається звичайним.
є функцією однієї незалежної змінної, то диференціальне рівняння називається звичайним. –рівняння першого порядку, а
–рівняння першого порядку, а  - рівняння другого порядку).
- рівняння другого порядку). або взагалі
або взагалі  , де
, де  і
і 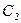 - сталі, є розв`язками рівняння
- сталі, є розв`язками рівняння (2.1)
(2.1) не є розв`язками рівняння (2.1).
не є розв`язками рівняння (2.1). (4.1)
(4.1) маємо
маємо . Далі маємо
. Далі маємо 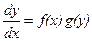 , або
, або (4.2)
(4.2) вважати функцією від
вважати функцією від  (4.3)
(4.3) , де
, де  . Тепер маємо
. Тепер маємо  .Це рівняння з відокремленими змінними. Інтегруючи, знайдемо загальний інтеграл диференціального рівняння.
.Це рівняння з відокремленими змінними. Інтегруючи, знайдемо загальний інтеграл диференціального рівняння.

 ):
):
 ,
,

 або
або 
 , (7.1)
, (7.1) і
і  неперервні функції (
неперервні функції ( ,
,  ), називається рівнянням Бернуллі.
), називається рівнянням Бернуллі. і добудемо
і добудемо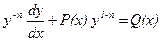 . (7.2)
. (7.2) ,
,  . Підставимо значення
. Підставимо значення  і
і у рівняння (7.2) і добудемо наступне лінійне рівняння:
у рівняння (7.2) і добудемо наступне лінійне рівняння: або
або  .
. вираз
вираз  , де
, де 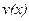 будь-який ненульовий розв`язок рівняння
будь-який ненульовий розв`язок рівняння .
. ,
,  .
. ,
,  .Підставивши у рівняння замість
.Підставивши у рівняння замість 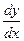 їх значення, одержимо
їх значення, одержимо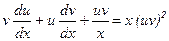 або
або  (7.3)
(7.3) маємо рівняння
маємо рівняння або
або  .
. або
або  .
.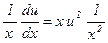 або
або  .
.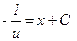 ,звідки
,звідки  .
. .
. , звідки
, звідки  .
.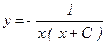 .
.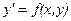 ?
? -го порядку має вигляд
-го порядку має вигляд  , тоді
, тоді (9.1)
(9.1) (9.2)
(9.2) та її частинні похідні по
та її частинні похідні по  неперервні в області
неперервні в області  , яка містить значення
, яка містить значення  , то існує єдиний розв`язок, який задовольняє початкові умови (9.2).
, то існує єдиний розв`язок, який задовольняє початкові умови (9.2). (
(

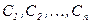 вона задовольняє диференціальному рівнянню;
вона задовольняє диференціальному рівнянню; , при яких ці умови виконуються.
, при яких ці умови виконуються. .
. .
.


