
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однорідні рівняння першого порядку.Содержание книги
Поиск на нашем сайте
Означення 1. Функція
Приклади. Функція
Функція
Означення 2. Диференціальне рівняння першого порядку
називається однорідним, якщо функція Розв`язання однорідного рівняння. Однорідна функція нульового виміру залежить лише від відношення змінних, бо
Зробимо підстановку Ми одержали рівняння з відокремлюваними змінними. Вважаємо, що Зауваження. Рівняння Приклад. Розв`язати рівняння Це рівняння є однорідним тому, що
Відокремлюючи змінні, знаходимо
Зінтегрувавши, одержимо
Підставивши
Знаходимо шуканий частинний розв`язок з початкових умов
Лінійні рівняння першого порядку.
Означення. Диференціальне рівняння першого порядку називається лінійним, якщо воно першого ступеня відносно шуканої функції та її похідної
де Розв`язання лінійного рівняння. Будемо шукати розв`язок лінійного рівняння у вигляді добутку двох шуканих функцій
Знайдемо похідну цієї функції
або
Виберемо функцію
Рівняння (6.4) – рівняння з відокремлюваними змінними. Відокремлюючи змінні, добудемо
Зінтегрувавши, знайдемо
Тому що нам потрібен будь-який ненульовий частинний розв`язок рівняння, покладемо
звідки
Підставимо замість
Приклад. Розв`язати рівняння Це рівняння є лінійним. Шукаємо розв`язок у вигляді
Підставимо
Знаходимо функцію
Зінтегрувавши рівняння, знаходимо
Знаходимо загальний розв`язок рівняння
Рівняння Бернуллі.
Означення. Диференціальне рівняння вигляду
де Зведемо рівняння Бернуллі до лінійного. Поділимо обидві частини рівняння (7.1) на
Зробимо заміну шуканої функції
Знаходимо загальний розв`язок останнього рівняння і підставимо замість Зауваження. Тому що рівняння Бернуллі зводиться до лінійного рівняння, його розв`язок можна шукати у вигляді
Приклад. Розв`язати рівняння Шукаємо розв`язок рівняння у вигляді
Для знаходження функції
звідки Підставивши знайдене значення
Зінтегрувавши, знаходимо Таким чином, загальний розв`язок рівняння
Знайдемо частинний розв`язок рівняння, який задовольняє заданим початковим умовам:
Підставимо знайдене значення довільної сталої у загальний розв`язок і добудемо шуканий частинний розв`язок:
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.163.91 (0.008 с.) |

 називається однорідною функцією
називається однорідною функцією  -го виміру, якщо для будь-якого
-го виміру, якщо для будь-якого  має місце тотожність
має місце тотожність
 - однорідна функція виміру
- однорідна функція виміру  , тому що
, тому що
 - однорідна функція нульового виміру, тому що
- однорідна функція нульового виміру, тому що
 (5.1)
(5.1) і якщо покласти
і якщо покласти  , то
, то 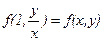 . Позначимо
. Позначимо 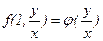 . Тоді рівняння (5.1) набуває вигляду
. Тоді рівняння (5.1) набуває вигляду (5.2)
(5.2) або
або  . Тоді маємо
. Тоді маємо  . Підставимо значення похідної в (5.2) і одержимо
. Підставимо значення похідної в (5.2) і одержимо  або
або 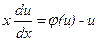 .
. , і відокремлюємо змінні
, і відокремлюємо змінні 
 звідки
звідки 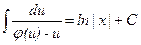 . Підставимо після інтегрування замість
. Підставимо після інтегрування замість 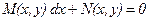 є однорідним, якщо функції
є однорідним, якщо функції  і
і  є однорідними функціями одного виміру.
є однорідними функціями одного виміру. ,
, 
 - однорідна функція нульового виміру: - однорідна функція нульового виміру:
- однорідна функція нульового виміру: - однорідна функція нульового виміру: . Покладемо
. Покладемо  . Тоді після підстановки у рівняння, одержимо рівняння з відокремлюваними змінними:
. Тоді після підстановки у рівняння, одержимо рівняння з відокремлюваними змінними: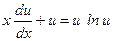 або
або 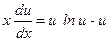 .
. або
або  .
. або
або  .
. , або
, або  , або
, або  .
. , звідки
, звідки  або
або 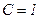 . Підставимо у загальний розв`язок
. Підставимо у загальний розв`язок 
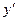 . Воно має вигляд
. Воно має вигляд (6.1)
(6.1) і
і  - неперервні функції.
- неперервні функції. і
і 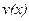 , тобто
, тобто (6.2)
(6.2)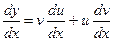 .Підставивши значення
.Підставивши значення 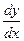 і
і  у рівняння (6.1), отримаємо
у рівняння (6.1), отримаємо
 (6.3)
(6.3) так, щоб
так, щоб (6.4)
(6.4)
 або
або  .
. , тобто
, тобто  . Тоді для визначення шуканої функції
. Тоді для визначення шуканої функції  маємо рівняння
маємо рівняння або
або  ,
, .
. або
або 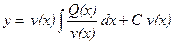 .
.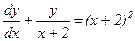 .
.
 або
або (6.5)
(6.5) . Відокремлюємо змінні, добуваємо
. Відокремлюємо змінні, добуваємо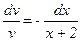 .
. . Поклавши
. Поклавши 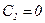 , добуваємо
, добуваємо  . Підставимо знайдене значення
. Підставимо знайдене значення  або
або  . Зінтегрувавши, одержимо
. Зінтегрувавши, одержимо .
. або
або 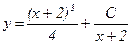 .
. , (7.1)
, (7.1) ,
,  ), називається рівнянням Бернуллі.
), називається рівнянням Бернуллі. і добудемо
і добудемо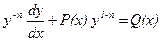 . (7.2)
. (7.2) ,
,  . Підставимо значення
. Підставимо значення  і
і у рівняння (7.2) і добудемо наступне лінійне рівняння:
у рівняння (7.2) і добудемо наступне лінійне рівняння: або
або  .
. вираз
вираз  .
. ,
,  .
. ,
,  .Підставивши у рівняння замість
.Підставивши у рівняння замість 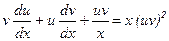 або
або  (7.3)
(7.3) або
або  .
. або
або  .
.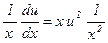 або
або  .
.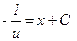 ,звідки
,звідки  .
. .
. , звідки
, звідки  .
.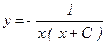 .
.


