
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки до лабораторних робіт. Фізичні основи механіки. Коливання та хвиліСодержание книги
Поиск на нашем сайте М І Н І С Т Е Р С Т В О О С В І Т И І Н А У К И У К Р А Ї Н И КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ТЕХНОЛОГІЙ ТА ДИЗАЙНУ МЕТОДИЧНІ ВКАЗІВКИ ДО ЛАБОРАТОРНИХ РОБІТ «Фізичні основи механіки. Коливання та хвилі» Для студентів всіх спеціальностей
ЗАТВЕРДЖЕНО на засіданні кафедри фізики протокол №10 від 04.06.05 р.
Київ - 2005 Методичні вказівки до лабораторних робіт. Фізичні основи механіки. Коливання та хвилі. А.П.Клименко, В.М.Клименко, Д.П.Літевчук, Б.М.Стаднік, М.Т.Степашко, А.О.Потапов, К.В.Авдонін.- Київ: КНУТД, 2005.- 50 с. Для студентів всіх спеціальностей
Відповідальний за випуск: Проф. А.П.Клименко
Методичні вказівки до лабораторних робіт з механіки, Механічних коливань та хвиль. Вступ Лабораторний практикум із курсу загальної фізики передбачає виконання циклів лабораторних робіт із механіки, механічних коливань та хвиль (N 1, 2, 3, 4, 40, 41, 43). Як у будь-якому досліді, результати та висновки лабораторних робіт повинні мати певний рівень наукового обґрунтування. Інакше така робота не має практичної цінності. Такий підхід до лабораторного практикуму закладає в інтелект майбутнього інженера певні основи дослідника-експериментатора, творчої інженерної наснаги і допитливості. Наявність багаточисельних похибок, що існують за межами нашого бажання та вміння, вимагає певних наукових підходів до опрацювання результатів вимірювань з метою отримання їх надійної оцінки. Завдання вступного розділу до лабораторного практикуму полягає в тому, щоб навчити студента передбачати та виключати певний клас похибок та обґрунтовувати отримані результати досліджень. Статистична обробка масиву результатів N прямих Вимірювань. 1. За істинне значення фізичної величини X приймається середньоарифметичне значення N вимірювань:
2. Визначається середньоквадратична похибка величини X:
3. Визначається середньоквадратичне відхилення результатів вимірювання від середнього значення
4. Визначається границя довірчого інтервалу X без врахування систематичної похибки
де 5. Визначається границя довірчого інтервалу X при заданій систематичній похибці
(15.0)
Остаточно результат прямого вимірювання записується, наприклад, у вигляді
Обробка результатів експерименту при посередніх Вимірюваннях. Нехай шукана фізична величина А визначається функціональною залежністю від k параметрів Xі
Спрощена методика статистичної обробки результатів вимірювань при визначенні фізичної величини А, що є функцією k величин Хі, які знаходяться прямими вимірами та обробляються за методикою п.2, для однакового значення довірчої імовірності Р, включає наступні кроки: 1. За істинне значення величини А приймається «середньоарифметичне»
2. Границя довірчого інтервалу визначається так:
3. У цьому виразі значень параметрів 4. Остаточно результат вимірювання записується, як і для прямих вимірювань, у вигляді
Правила побудови графічних залежностей фізичних величин. Лабораторна робота №1 Визначення густини речовини тіла Прилади та обладнання. 1. терези з вижками; 2. штангенциркуль; 3. набір тіл циліндричної форми. Хід виконання роботи 1. Визначити масу m тіла, зважуючи його на технічних вагах. Вимір зробити 5-7 разів. 2. Штангенциркулем виміряти діаметр d досліджуваного циліндра. Виміри повторити 5-7 разів на різних рівнях від основи, повертаючи щоразу циліндр навколо осі. 3. Штангенциркулем виміряти висоту h досліджуваного циліндра. Виміри повторити 5-7 разів, повертаючи щораз циліндр навколо осі. 4. Результати вимірів занести в Таблицю 1.1.
Оцінками істинного значення виміряних величин m, h,d будуть їх середньоарифметичні значення Питому густину з урахуванням (1.1., 3.1) та данних Таблиці 1.1. знаходимо за формулою
Довірчу межу виміряної величини знаходимо, використовуючи методику опрацювання результатів непрямих (посередніх) вимірів (див.розділ 3) за формулою
Виміряне значення питомої густини запишемо так
Використання Мсad: ПрикладвикористанняМсad для знаходження величин r, Dr, наведений в методичному посібнику [4.1]. Контрольні запитання 1. Що таке «густина речовини» і як вона може бути визначена? 2. Які похибки вимірювання методичного характеру притаманні застосованому в лабораторній роботі методу визначення густини? 3. Що таке інструментальна похибка вимірювання і як її оцінити? 4. Яка різниця між поняттям «похибка вимірювання» і «границя довірчого інтервалу похибки»? 5. В чому полягає суть поняття «прямі виміри» і в який спосіб оцінюється довірчий інтервал виміряної величини при прямих вимірах? 6. В чому полягає суть метода визначення границі довірчого інтервалу похибки вимірювання при непрямих (посередніх) вимірах?
Література
1.1. Зайдель А. Н. Ошибки измерений физических величин. Л.: Наука, 1974,-108 с. 2.1..Бурдун Г. Д., Марков Б. Н. Основы метрологии. 2-е изд. М.: Изд-во стандартов, 1975.- 335 с. 3.1. Трофимова Т.И. Курс физики. – М.: Высш. шк., 2000. – 478 с. 4.1..Опрацювання результатів вимірювання при виконанні лабораторних робіт фізичного практикума з використанням математичної системи Mcad. (Методичні вказівки до лабораторного практикуму для студентів усіх спеціальностей). А.О.Потапов, А.І.Мотіна. - К.: КНУТД, 2004.- 112 с.
Лабораторна робота №2 Хід виконання роботи Пружне зіткнення куль. 1. Включити «Блок керування та індикації» натисканням кнопки «Мережа (Сеть)»; 2. Натиснути кнопку«Сброс» аби встановити на цифровому табло нульові покази; 3. Поставити кнопку «Пуск» у виключений стан (відтиснуто) при цьому включається електромагніт; 4. Перевірити початкове положення куль (установка нулів), провести їх центрування, у результаті якого поверхні куль повинні дотикатися, а їхні центри лежати на одній горизонталі в площині дуги шкального пристою; 5. Відхилити кулю маси 6. Натиснути кнопку «Пуск», розімкнувши коло живлення електромагніта, і вимірити значення кутів a' і b, на які відхиляться кульки після удару та тривалость удару t. Ці виміри повторити не менше 7 разів. Отримані результати записати в Таблицю 1.2 7. Розрахувати середньоарифметичні значення кутів відхилення куль
УВАГА! При розрахунках треба мати на увазі, що величини Таблиця 1.2
8..За результатами вимірювань розрахувати значення імпульсу системи до Q і після удару R, величину коефіцієнта відновлення енергії К, середньої сили взаємодії F та межі їх довірчіх інтервалів. Результати розрахунків занести в Таблицю 1. Лабораторна робота №3 Лабораторна робота № 4
Визначення моменту інерції тіла методом крутильних коливань
Мета роботи · визначити момент інерції тіла складної геометричної форми Теоретичні відомості. Момент інерції макроскопічного тіла можна знайти розбиттям тіла на нескінченно малі маси
Тобто, момент інерції однорідного тіла правильної геометричної форми можна визначити розрахунково із (1.4). Моменти інерції тіл складної геометричної форми за звичай визначають експериментально. Одним із методів експериментального визначення моменту інерції тіла є метод Гауса, заснований на використанні обертальних чи крутильних коливань.
За другим законом Ньютона для обертового руху, рівняння коливань маятника можна записати так:
Вектори
і в канонічному вигляді:
де
Період вільного гармонічного коливання тим більше, чим більше момент інерції тіла і чим менша пружність стержня (дроту), на якій воно закріплене. Виміривши період Т крутильних коливань, можна визначити момент інерції тіла, яке здійснює ці коливання. Однак для цього необхідно знати модуль крутіння f. Метод Гауса полягає в застосуванні крутильних коливань і виключенні невідомого значення модуля крутіння f з використанням пробного (еталонного) тіла з відомим моментом інерції. Період коливань вимірюють двічі: а) для досліджуваного тіла, для якого період коливань маятника
б) для тіла, складеного з досліджуваного тіла з моментом інерції Jх і пробного (еталонного) тіла з моментом інерції J. якщо їх центри мас знаходяться на вісі обертання, період коливань складеного тіла визначається за формулою,
Звівши обидві частини виражень для періодів у квадрат і, поділивши одне на друге, одержимо пропорцію
з якої випливає
Момент інерції пробного (еталонного) тіла J, в якості якого, як правило, вибирають однорідне тіло провильної геометричної форми (куля, циліндричне кільце, куб, паралеліпіпед та інш.) тому, що його момент інерції можна розрахувати за формулою (1.4). На приклад, момент інерції циліндричного кільця відносно вісі, що співпадає з геометричною віссю, дорівнює
де R і r - відповідно зовнішній і внутрішній радіуси кільця, а d1 і d2 їхні діаметри, m ¾ маса кільця. Момент інерції суцільного однорідного циліндра масою m і радіуса R відносно вісі, що співпадає з геометричною віссю, дорівнює
Куля масою m і радіуса R має момент інерцї
Геометричні розміри пробного тіла вимірюють штангенциркулем, а масу знаходять зважуванням на вагах. Періоди коливань Т1 і Т2 досліджуваного й складного тіла визначають, вимірюючи час N =10¸20 коливань секундоміром (t1 і t2). Хід виконання роботи Завдання 1.Визначення величини моменту інерції тіла складної геометричної форми(рамки крутильного маятника). 1. Вимірювання періоду коливань рамки без пробного тіла: 1.1. Приєднати установку до електричної мережі 220 В, 50 Гц і ввімкнути блок живлення та індикації, натиснувши кнопку «Мережа(Сеть)»; 1.2. Встановити на нульові позначки цифрові індикатори натисканням кнопки «Сброс», а кнопка «Пуск» повинна бути у відтиснутому стані; 1.3. Повернути рамку таким чином, щоб прапорець був притягнутий електромагнітом і надали його положення було зафіксоване; 1.4. Почати вимірювання часу коливань натисканням кнопки «Пуск»; 1.5. Відрахувати за показаннями індикатора задане число періодів коливань (N =10¸20) і виключити лічильник і секундомір натисканням кнопки «Стоп»; Увага! Кнопку «Стоп» слід натискатипісля того, як лічильник покаже число на одиницю менше заданого (N -1), секундомір виключиться автоматично після виконання N коливань; 1.6. Виміри повторити 5-7 разів і занести в Таблицю 1.4; 2. Вимірювання періоду коливань рамки із пробним тілом: 2.1. Закріпити пробне тіло в рамці; 2.2. Виконати вимірювання відповідно до п.п.1.2-1.6. Таблиця 1.4
3. Момент інерції пробного тіла розраховується за формулами (6.4-8.4) в залежності від геометричної форми тіла. 4. Довірчі межі похибок вимірів маси й геометричних розмірів пробного тіла визначаються за правилами обробки прямих вимірів. Невиключені залишки систематичних похибок q прийняти рівними інструментальній похибці приладів. 5. Довірчі межі найбільшімовірних значень моменті інерції пробних тіл визначаємо за формулами для кільця для суцільного циліндра та кулі 6. Момент інерції рамки розраховується за формулою (9.4); 7. Довірчі межі найбільшімовірних значень моменту інерції рамки визначаємо за формулою
ЛІТЕРАТУРА 1.4. Кучерук І.М., Горбачук І.Т., Луцик П.П.. Загальний курс фізики: Навчальний посібник. –Т. 1.: Механіка. Молекулярна фізика і термодинаміка. – К.: Техніка, 1999. – 536 с. 2.4. Дущенко В.П., Кучерук І.М. Загальна фізика. Фізичні основи механіки. Молекулярна фізика і термодинаміка. – К.: Вища школа, 1993. – 431 с. 3.4. Загальна фізика. Лабораторний практикум: Навч. посібник за заг.ред. І.Т. Горбачука. – К.: Вища школа, 1992. – 509 с. 4.4. Трофимова Т.И. Курс физики. – М.: Высш. шк., 2000. – 478 с. 5.4. Опрацювання результатів вимірювання при виконанні лабораторних робіт фізичного практикума з використанням математичної системи Mcad. (Методичні вказівки до лабораторного практикуму для студентів усіх спеціальностей). А.О.Потапов, А.І.Мотіна. - К.: КНУТД, 2004.- 112 с.
Лабораторна робота № 40
Мета роботи · визначити величину прискорення сили тяжіння Землі. Теоретичні відомості.
Величину моменту сили тяжіння можна записати у вигляді
де J=mL2 ¾ момент інерції точкового тіла. Вектори
В канонічному вигляді це рівняння має вигляд:
де Таким чином, період власних коливань визначається так
У цьому виразі g ¾ прискорення сили тяжіння Землі або як кажуть прискорення вільного падіння. Із закону всесвітнього тяжіння Ньютона можна показати що
g=9,8 м/с2. З формули (1) випливає, що залежність довжини маятника L від періоду коливань T можна записати так
Якщо покласти
то вираз (3) можна лініаризувати
Екпериментальна установка. Експериментальна установка для визначення величини прискорення вільного падіння (Рис.2.40) складається з основи, на якій встановлені блок живлення та керування і стійка, в верхній частині якої знаходиться кронштейн із спеціальним блоком для кріплення нитки підвіса маятника із тілом маятника. Довжину маятника можна визначати по міліметровій лінійці, що закріплена на стійці. На стійці змонтована ще один кронштейн, на якому розташований електооптичний датчик блока живлення і керування. На передній панелі блока живлення та керування знаходяться: кнопка «Мережа(Сеть)» для вмикання установки, кнопка «Сброс» для установки на нуль показань цифрових індикаторів, кнопка «Стоп» для зупинки процесу вимірювання, цифрові індикатори числа коливань маятника і часу коливань. Установка працює таким чином: В початковому(до включення) - рівноважному стані, встановлюється певна довжина підвісу маятника шляхом обертання блока на кронштейні; кронштейн з електооптичним датчиком розташовується так, щоб оптична вісь датчика знаходилась на одній горизонталі з центром тіла маятника за відповідними мітками на корпусі датчика, а тіло маятника – між освітлювачем і приймачем датчика; після приєднання блока живлення та індикації до електричної мережі і включення його натисканням кнопки «Мережа(Сеть)», маятник відхиляють на кут (5-15)0 і утримуючи його, встановнюють на нульові позначки цифрові індикатори натисканням кнопки «Сброс», а потім відпускають маятник, який рухаючись, здійснює вільні коливання; секундомір блока живлення та керування починає відлік часу коливань тому, що в процесі коливань тіло маятника перетинає оптичне коло датчика, оночасно включаючи лічильник кількості періодів коливань, число яких висвітлюється індикатором; процес вимірювання зупиняється натисканням кнопки «Стоп». Хід виконання роботи 1. Встановити максимальну довжину L нитки підвісу маятника і значення довжини занести до Таблиці 1.40.; 2. приєднати блок живлення та індикації до електричної мережі і включити його натисканням кнопки «Мережа(Сеть)»; 3. маятник відхилити на кут (5-15)0 і утримуючи його, встановити на нульові позначки цифрові індикатори натисканням кнопки «Сброс»; 4. відпустити маятник і провести вимірювання часу N = 10 повних коливань t, результат занести в Таблицю 1.40; Увага! Кнопку «Стоп» слід натискатипісля того, як лічильник покаже число на одиницю менше заданого (N -1), секундомір виключиться автоматично після виконання N коливань; 5. Виконати вимірювання за п.п.3,4 для 5-7 різних довжин підвісу, а результати вимірювання часу t коливань занести до Таблиці 1.40 Таблиці 1.40
Лабораторна робота № 41-1. Мета роботи. Дослідити згасаючі коливання фізичного маятника і за виміряним числом повних коливань Nt і часу релаксації t обчислити: · сталу згасання g, · коефіцієнт опору r, · логарифмічний декремент згасання l, · добротність коливальної системи Q, оцінити коефіцієнт тертя кочення. Теоретичні відомості:
Використовуючи другий закон Ньютона для обертового руху, рівняння коливань можна записати так:
де J ¾ момент інерції тіла. Вектори
В канонічному вигляді рівняння (2.41) можна записати так
де Розв'язок (3.41) шукаємо підстановкою Ейлера j=elt. Знайдемо перші дві похідні від j по часу
Підставляючи похідні (4.41) в (3.41), одержимо: elt (l2 + 2gl + w02 ) = 0. (5.41) Квадратне рівняння l2 + 2gl + w02 = 0 в (5.41) називається характеристичним. Його розв'язок
дає два фундаментальні розв'язки диференціального рівняння j1 = exp(l1t), j2 = exp(l2t), (7.41) з яких утворюється загальний розв'язок. Загальним розв'язком однорідного рівняння (3.41) буде лінійна комбінація фундаментальних розв'язків j = Аexp(l1t) + Bexp(l2t) (8.41) з дійсними коефіцієнтами А, В. Якісно розрізняють два випадки руху маятника: 1) При g > w0 ¾ аперіодичний рух. При цьому l1,l2 < 0 ¾ дійсні числа. Функція j є спадною функцією часу (l1,l2<0) і описує асимптотичне, в експоненційній залежності від часу, повернення маятника в стан рівноваги. При цьому коливальний рух не здійснюється. 2) Якщо g < w0, маятник буде здійснювати коливальний рух. При цьому l1 = - g+іw, l2 = - g-іw, (9.41) де і = j = e-gt(Aeiwt+ Be-iwt) (10.41) з комплексними коефіцієнтами А, В. Для знаходження величин А та В зауважимо, що функція j є дійсною функцією часу, і за цим вона має дорівнювати своїй комплексно спряженій функції j = j* Þ e-gt(Aeiwt+Be-iwt) = e-gt(A*e-iwt +B*eiwt). (11.41) Прирівнюючи в (11.41) коефіцієнти при однакових експонентах, одержимо В=А *. Для зручності комплексну сталу А візьмемо в експоненціальному вигляді А = а0eia/2, де а0 ¾ дійсна величина. Тепер j = а0/2·e-gt (ei(wt+a) +e-i(wt+a)) (12.41) і, користуючись формулою Ейлера e±ix = cosx ± i×sinx, вираз в дужках запишемо у вигляді: j = j = j0(t)×cos(wt+a). (13.41) В (13.41) j0(t) = a0e-gt ¾ амплітуда коливань ¾ спадна функція часу, Ф = wt+a ¾ фаза коливань, Ф0 = a ¾ початкова фаза. Лабораторна робота № 43
Мета роботи: Визначити · швидкість звуку у повітрі; · сталу адіабати повітря. Теоретичні відомості: Звук – це процес розповсюдження коливань в пружному середовищі, наприклад в повітрі; молекули повітря, коливаючись, створюють області стиснення – розрідження, які розповсюджуються з певною швідкістю – швидкістю звуку. Очевидно, що швидкість звуку має залежати від складу і стану повітря. Якщо вважати повітря «ідеальним газом», то з точки зору термодинаміки процес розповсюдження коливань в пружному середовищі без втрат можна вважати адіабатним через те, що за характеристичний час процесу – період коливань, кінетична енергія спрямованого руху молекул повністю перетворюється в потенційну енергію їх взаємного положення і навпаки, тобто повітря як термодинамічна система не отримує додаткової теплоти від джерела звуку ΔQ=0. З огляду на це швидкість звуку V може бути визначена формулою Лапласа
де Р – тиск повітря, ρ – його густина, γ = СР/СV – стала адіабати, що визначається відношенням теплоємності повітря в ізобарному СР до теплоємності в ізохорному процесі СV. З урахуванням рівняння стану ідеального газу (рівняння Менделеєва – Клайперона) сталу адіабати можна визначити через швидкість звуку
в цьому рівнянні μ – молярна маса повітря; R – універсальна газова стала; Т – температура повітря. В даній лабораторній роботі швидкість повітря визначається методом «стоячої хвилі». Суть метода полягає в наступному: якщо в деякому замкненому об'ємі сформувати дві когерентні звукові хвилі А1(ω,х) і А2(ω,х) з приблизно однаковими амплітудами А01 »А02 і довжиною хвилі λ, які б розповсюджувались вздовж вісі ох в протилежних напрямках, то в результаті їх інтерференції виникне результуюча хвиля А з цікавими властивостями, а саме:
в результаті інтерференції цих хвиль отримаємо коливальний процес, амплітуда якого залежить від координати вздовж вісі розповсюдження звуку. Тобто в певних точках ХМАХ, що відповідають умові Важливою особливістю «стоячої хвилі» є те, що середній потік енергії хвилі вздовж вісі розповсюдження формально дорівнює нулю; насправді просто потік енергії, що переноситься хвилею в одному напрямку приблизно дорівнює потоку енергії, що переноситься хвилею в протилежному напрямку. Оскільки існування «стоячої хвилі» супроводжується зростанням амплітуди коливань в певних точках ХМАХ, для цих точок вводять поняття «квазірезонанс», умовою якого є
З умови (4.43) випливає, що «квазірезонанс» може бути досягнутий вибором частоти звуку ν=ω/2π при незмінній точці відліку, або довжині шляху розповсюдження хвилі, або зміною довжини шляху розповсюдження хвилі L при незмінній частоті звуку. Таким чином метод «стоячої хвилі» для визначення швидкості звуку в повітрі може бути здійснений або при постійній довжині замкненого об'єму (метод постійної довжини), який називають «звуковою трубою», і змінній частоті звуку, або при постійній частоті (метод постійно
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.014 с.) |

 . (11.0)
. (11.0) . (12.0)
. (12.0)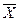 :
: . (13.0)
. (13.0) Х (інструментальна похибка приладу, яким вимірюється X)
Х (інструментальна похибка приладу, яким вимірюється X) . (14.0)
. (14.0) - табличний коефіцієнт Сть'юдента, для числа вимірювання n та імовірності
- табличний коефіцієнт Сть'юдента, для числа вимірювання n та імовірності  (див.Таблицю1.0)
(див.Таблицю1.0)
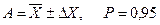 . (16.0)
. (16.0) . (17.0)
. (17.0) . (18.0)
. (18.0)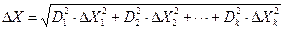 . (19.0)
. (19.0) — частинна похідна, обчислена для середніх
— частинна похідна, обчислена для середніх .
. Таблиця 1.1.
Таблиця 1.1.



 разом з обчисленими довірчими інтервалами
разом з обчисленими довірчими інтервалами 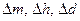 по методиці (див.розділ 2) опрацювання результатів прямих вимірів. Результати розрахунків занести в Таблицю 1.1.
по методиці (див.розділ 2) опрацювання результатів прямих вимірів. Результати розрахунків занести в Таблицю 1.1.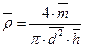 . (4.1)
. (4.1) . (5.1)
. (5.1) . (6.1)
. (6.1) на кут
на кут 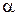 і зафіксувати її положення електромагнітом.
і зафіксувати її положення електромагнітом. і часу зіткнення
і часу зіткнення  та їх межі довірчіх інтервалів як результати прямих вимірів. Результати розрахунків занести в Таблицю 1.2
та їх межі довірчіх інтервалів як результати прямих вимірів. Результати розрахунків занести в Таблицю 1.2 в розрахункових формулах (19.40 – 28.40), необхідно підставляти в
в розрахункових формулах (19.40 – 28.40), необхідно підставляти в 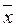
 і розглянути їх як точкові. При цьому момент інерції тіла дорівнює сумі моментів інерції його складових
і розглянути їх як точкові. При цьому момент інерції тіла дорівнює сумі моментів інерції його складових або для однорідного тіла
або для однорідного тіла  . (1.4)
. (1.4) Крутильний маятник ¾ макроскопічне тіло з моментом інерції J, закріплене нерухомо на пружному стержні (Рис.1.4). Коливання визначаються кутом відхилення
Крутильний маятник ¾ макроскопічне тіло з моментом інерції J, закріплене нерухомо на пружному стержні (Рис.1.4). Коливання визначаються кутом відхилення  тіла від положення рівноваги, вектором кутової швидкості
тіла від положення рівноваги, вектором кутової швидкості  та вектором кутового прискорення
та вектором кутового прискорення  . Тіло здійснює малі періодичні коливання під дією моменту
. Тіло здійснює малі періодичні коливання під дією моменту  зовнішньої сили
зовнішньої сили  , моменту
, моменту  сили опору
сили опору  та моменту
та моменту  пружної сили деформації кручення
пружної сили деформації кручення  . Кефіцієнт f називається модулем кручення. Лінійна залежність моменту сил кручення від кута повороту виконується лише для малих коливань.
. Кефіцієнт f називається модулем кручення. Лінійна залежність моменту сил кручення від кута повороту виконується лише для малих коливань. . (2.4)
. (2.4) лежать на одній прямій, а тому, взявши напрямок кутового прискорення
лежать на одній прямій, а тому, взявши напрямок кутового прискорення  за додатній, векторне рівняння (2.4) можна записати в алгебраїчній формі:
за додатній, векторне рівняння (2.4) можна записати в алгебраїчній формі: ,
, , (3.4)
, (3.4) ¾ коефіцієнт згасання коливань,
¾ коефіцієнт згасання коливань,  , w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника
, w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника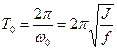 . (4.4)
. (4.4) ,
, .
.
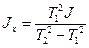 . (5.4)
. (5.4) , (6.4)
, (6.4) . (7.4)
. (7.4)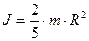 . (8.4)
. (8.4) (сек)
(сек) (сек)
(сек)
 ,
, .
.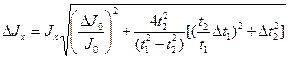 .
. Математичний маятник (Рис.1.40) ¾ точкове тіло масою m, підвішене на нерозтяжному підвісі L, розмірами якого, порівнюючи з довжиною підвісу, можна знехтувати. Маса підвісу значно менша маси тіла m. Коливання описуються кутом відхилення тіла від положення рівноваги ¾
Математичний маятник (Рис.1.40) ¾ точкове тіло масою m, підвішене на нерозтяжному підвісі L, розмірами якого, порівнюючи з довжиною підвісу, можна знехтувати. Маса підвісу значно менша маси тіла m. Коливання описуються кутом відхилення тіла від положення рівноваги ¾  . Вектор
. Вектор  задає точку прикладання сил. Коливання здійснюються в загальному випадку під дією моменту
задає точку прикладання сил. Коливання здійснюються в загальному випадку під дією моменту 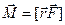 зовнішніх сил
зовнішніх сил 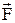 , моменту сили тяжіння
, моменту сили тяжіння  та моменту сил опору
та моменту сил опору 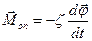 , де
, де  ¾ коефіцієнт опору. Вектори моментів сил
¾ коефіцієнт опору. Вектори моментів сил  та кутового прискорення
та кутового прискорення  . Для малих коливань j маємо sinj» j і
. Для малих коливань j маємо sinj» j і  . За другим законом Ньютона рівняння коливань можна записати так
. За другим законом Ньютона рівняння коливань можна записати так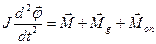 ,
, лежать на одній прямій, а тому, взявши напрямок кутового прискорення за додатній, векторне рівняння можна записати в алгебраїчній формі
лежать на одній прямій, а тому, взявши напрямок кутового прискорення за додатній, векторне рівняння можна записати в алгебраїчній формі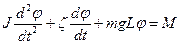 .
.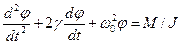 ,
,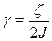 ¾ коефіцієнт згасання коливань,
¾ коефіцієнт згасання коливань,  , w0 ¾ частота вільних незгасаючих коливань, або частота власних коливань маятника.
, w0 ¾ частота вільних незгасаючих коливань, або частота власних коливань маятника. . (1.40)
. (1.40)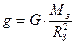 , (2.40)
, (2.40)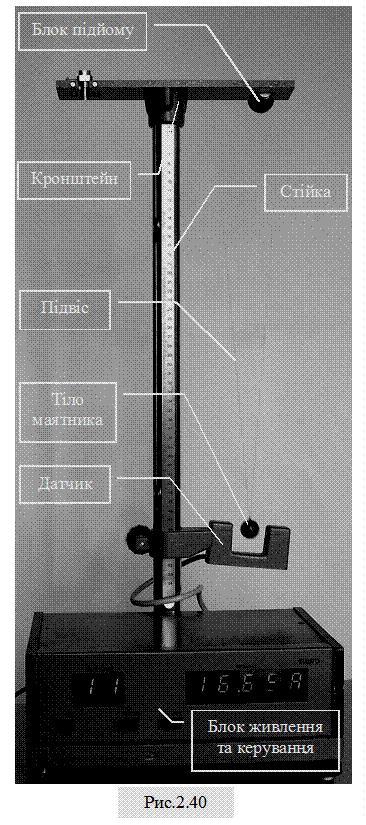 де GЗ=6,67×1011 Н×м2/кг2 – гравітаційна стала, МЗ=5б976×1024 кг ¾ маса Землі, RЗ=6,4×106 м ¾ радіус Землі, L ¾ довжина підвісу маятника. Підрахунок за формулою (2) дає величину прискорення сили тяжіння рівною
де GЗ=6,67×1011 Н×м2/кг2 – гравітаційна стала, МЗ=5б976×1024 кг ¾ маса Землі, RЗ=6,4×106 м ¾ радіус Землі, L ¾ довжина підвісу маятника. Підрахунок за формулою (2) дає величину прискорення сили тяжіння рівною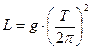 (3.40)
(3.40) , (4.40)
, (4.40) . (5.40)
. (5.40)
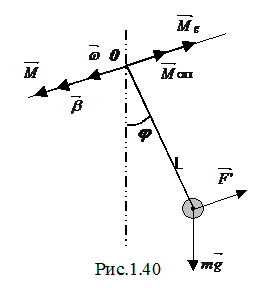
 Фізичний маятник ¾ макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла Oc на вектор
Фізичний маятник ¾ макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла Oc на вектор  . Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту
. Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту  зовнішніх сил
зовнішніх сил  , моменту сили тяжіння
, моменту сили тяжіння  , де
, де  ¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: Мg = mgLsinj. Для малих коливань маятника маємо sinj» j і Мg = mgLj.
¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: Мg = mgLsinj. Для малих коливань маятника маємо sinj» j і Мg = mgLj. лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі:
лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі: . (2.41)
. (2.41) ¾ коефіцієнт згасання коливань,
¾ коефіцієнт згасання коливань,  , w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника T0 = 2p/w0 і T0 = 2p
, w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника T0 = 2p/w0 і T0 = 2p  , де lпр =
, де lпр =  ¾ приведена довжина фізичного маятника. Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору (3.41)
¾ приведена довжина фізичного маятника. Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору (3.41)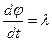 elt,
elt,  = l2elt. (4.41)
= l2elt. (4.41) ,
,  (6.41)
(6.41) ¾ уявна одиниця, w =
¾ уявна одиниця, w =  ¾ частота вільних згасаючих коливань. Загальний розв'язок буде мати вигляд:
¾ частота вільних згасаючих коливань. Загальний розв'язок буде мати вигляд: а0e-gt [cos(wt+a)+i×sin(wt+a)+cos(wt+a)-i×sin(wt+a)] Þ
а0e-gt [cos(wt+a)+i×sin(wt+a)+cos(wt+a)-i×sin(wt+a)] Þ . (1.43)
. (1.43) . (2.43)
. (2.43)
 (3.43)
(3.43) , амплітуда коливань досягатиме подвійного значення (пучність хвилі), а в точках ХМІN, що відповідають умові
, амплітуда коливань досягатиме подвійного значення (пучність хвилі), а в точках ХМІN, що відповідають умові  , амплітуда коливань дорівнюватиме нулю (вузол хвилі); n = 1,2,3…. На перший вигляд маємо справу не з хвильовим процесом, а з чисто коливальним, через що це явище отримало назву «стояча хвиля».
, амплітуда коливань дорівнюватиме нулю (вузол хвилі); n = 1,2,3…. На перший вигляд маємо справу не з хвильовим процесом, а з чисто коливальним, через що це явище отримало назву «стояча хвиля».
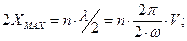 оскільки
оскільки  . (4.43)
. (4.43)


