
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вивчення динаміки обертового рухуСодержание книги
Поиск на нашем сайте
Мета роботи: 1. Перевірити справедливість основного закону обертового руху за допомогою «маятника Обербека»; 2. Визначити величину моменту інерції «маятника Обербека» і його залежність від розподілу мас відносно вісі обертання; 3. Визначити величину моменту сили опору рухові маятника.
Теоретичні відомості: Маятник Обербека являє собою циліндричне тіло із шківом на осі радіусу r та 4-ма однаковими взаємно перпендикулярними стержнями. На стержнях пристосовані пересувні важки масою m0 кожний. Вони розташовані на відстані R від центру маятника (див. Рис.1.3.). Стержні лежать у площині ^ осі циліндра і проходять через центр маятника. Маятник приводиться в обертовий рух тягарцем m із ниткою, намотаною на шків. Вісь обертання співпадає з віссю циліндра. Спочатку тягарець, опускаючись, за рахунок сили натягу нитки За час опускання t та підйому t¢ маятник повертається на кут
можна записати в алгебраїчному вигляді
В цьому рівнянні
можна записати в алгебраїчному вигляді
Таким чином ми одержали першу пару рівнянь руху маятника Обербека:
Рух тягарця рівноприскорений і тому
Для знаходження моменту інерції маятника J, помножимо рівняння (2) на r і додамо ліві та праві частини рівнянь (1.3-2.3). В результаті одержимо
Підставимо в (4.3)
В (5.3) залишається невідомим момент сили тертя. Знайдемо його з того, що робота проти сили тертя дорівнює
Робота виконується за рахунок зменшення потенціальної енергії тягарця на величину Момент інерції J є сумою моменту інерції власне хрестовини маятника J0 та моменту інерції 4-х важків m0, які можна вважати точковими, і тоді
Таким чином, досліджуючи рух маятника спершу з тягарцем масою m1, а потім - m2 (m2≠ m1) і враховуючи вирази (1.3-2.3), можна стверджувати
Використовуючи (2.3-3.3), після нескладних перетворень, отримаємо
Зверніть увагу, що
Визначивши момент інерції маятника, навіть не досліджуючи процес його коливання, лише вимірявши час опускання тягарця, можна досить точно оцінити величину моменту сили тертя (сили опору) МТР. Використовуючи (2.3-5.3) простими підстановками і перетвореннями отримаємо
Наведений теоретичний аналіз закономірностей руху маятника Обербека дозволяє шляхом прямих вимірів на експериментальній установці і наступних розрахунків досягти мети роботи. Експериментальна установка. Зовнішній вигляд і склад установки показано на Рис.2.3.Експериментальна
Управління установкою здійснюється за допомогою кнопок, які розташовані на передній панелі блока керування та індикації: кнопка «Мережа(сеть)» включає живлення блоку; кнопкою «Сброс» встановлюються на нульову позначку показання цифрового індикатора часу – секундоміра; натискання кнопки «Пуск», яка у вихідному положенні попередньо має бути відтиснута, розриває коло живлення електромагнітного гальма і тягарець набувши можливості рухатись, минаючи положення датчика 1, включає електронний секундомір, а коли він досягає положення датчика 2, робота секундоміру зупиняється і включаюється електромагнітне гальмо, яке зупиняє рух тягарця. На цифровому табло висвічується значення часу, на протязі якого тягарець опускався до низу. Експериментальні дослідження. Завдання 1. Перевірити справедливість основного закону обертового руху. Із виразів (1.3), (9.3), (10.3) випливає, що квадрат часу руху тягарця пропорційний його масі, тому, якщо змінювати масу тягарця, то має бути справедливо
Тому, якщо між масою тягарця mі і величиною, що пропорційна квадрату часу Завдання 2. Визначити величину моменту інерції маятника і його залежність від розподілу мас відносно вісі обертання. Величину моменту інерції визначають за виразом (11.3), вимірюючи час руху тягарця при його незмінній масі.
Завдання 3. Визначити величину моменту сили опору рухові МТР - моменту сили тертя. Момент сили тертя визначають за формулою (12.3) шляхом вимірювання часу руху маятника при незмінному значенні моменту інерції (R = Соnst).
Виконання вимірювань: 1. Закріпити пересувні важки m0 на мінімальній відстані R від вісі обертання маятника; 2. Підключити блок керування та індикації до електричної мережі 220 В, 50 Гц; кнопкою «Сброс» встановити на нульову позначку показання цифрового індикатора часу – секундоміра; кнопка «Пуск» має бути відтиснута; 3. Підняти тягярець на висоту h шляхом намотування нитки на шків; 4. Натиснути кнопку «Пуск», дати змогу тягарцю опускатись і виміряти час його руху з висоти h; 5. Виміри виконати 5-7 разів і результати вимірювання занести в Таблицю 1.3; 6. Закріпити тягарець іншої маси і виконати виміри за п.п. 3-5; 7. виконати виміри за п.п. 3-5 для тягарця іншої маси; 8. виконати виміри за п.п. 3-5 для 3-5 значень відстані R важків m0 від вісі обертання при незмінній масі тягарця; 9. Результати вимірів занести в таблицю1.3 Таблиця 1.3
10. За результатами вимірювань виконати розрахунки моменту інерції J та моменту сили тертя МТР ; 11. Оцінку межі довірчого інтервалу розрахованого значення моменту інерції J можна здійснити за формулою
12. Оцінку межі довірчого інтервалу розрахованого значення моменту сили тертя МТР можна здійснити за формулою
13. За результатами розрахунків побудувати графік залежності між масою mі і квадратом часу зробити висновок про справедливість основного закону обертового руху; 14. За результатами розрахунків побудувати графік залежності між величиною моменту інерції J і R2, оцінити характер кореляції між змінними і зробити висновок щодо залежності величини моменту інерції маятника від розподілу мас відносно вісі обертання.
Для розрахунків за формулами (11.3-15.3) можна застосувати програмні системи Excel, Мсad, ORIGIN та інш.,. Використання Мсad: ПрикладвикористанняМсad для знаходження величини прискорення вільного падіння наведений в методичному посібнику [6.3].
Контрольні запитання 1. Дайте визначення векторів повороту dj, кутової швидкості w, кутового прискорення e. 2. Дайте визначення моментів сили та імпульсу. 3. Доведіть вираз для моменту імпульсу 4. Дайте визначення моменту інерції J точкового тіла та макроскопічного тіла. 5. Запишіть теорему Штейнера. 6. Виведіть рівняння обертового руху Ньютона
ЛІТЕРАТУРА 1.3. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: Навчальний посібник. –Т. 1.: Механіка. Молекулярна фізика і термодинаміка. – К.: Техніка, 1999. – 536 с. 2.3..Дущенко В.П., Кучерук І.М. Загальна фізика. Фізичні основи механіки. Молекулярна фізика і термодинаміка. – К.: Вища школа, 1993. – 431 с. 3.3..Загальна фізика. Лабораторний практикум: Навч. посібник за заг.ред. І.Т. Горбачука. – К.: Вища школа, 1992. – 509 с. 4.3..Д.В. Сивухин. Общий курс физики. Т. І. Механика. – М.: Наука, 1989. – 576 с. 5.3..Трофимова Т.И. Курс физики. – М.: Высш. шк., 2000. – 478 с. 6.3.. Опрацювання результатів вимірювання при виконанні лабораторних робіт фізичного практикума з використанням математичної системи Mcad. (Методичні вказівки до лабораторного практикуму для студентів усіх спеціальностей). А.О.Потапов, А.І.Мотіна. - К.: КНУТД, 2004.- 112 с.
Лабораторна робота № 4
Визначення моменту інерції тіла методом крутильних коливань
Мета роботи · визначити момент інерції тіла складної геометричної форми Теоретичні відомості. Момент інерції макроскопічного тіла можна знайти розбиттям тіла на нескінченно малі маси
Тобто, момент інерції однорідного тіла правильної геометричної форми можна визначити розрахунково із (1.4). Моменти інерції тіл складної геометричної форми за звичай визначають експериментально. Одним із методів експериментального визначення моменту інерції тіла є метод Гауса, заснований на використанні обертальних чи крутильних коливань.
За другим законом Ньютона для обертового руху, рівняння коливань маятника можна записати так:
Вектори
і в канонічному вигляді:
де
Період вільного гармонічного коливання тим більше, чим більше момент інерції тіла і чим менша пружність стержня (дроту), на якій воно закріплене. Виміривши період Т крутильних коливань, можна визначити момент інерції тіла, яке здійснює ці коливання. Однак для цього необхідно знати модуль крутіння f. Метод Гауса полягає в застосуванні крутильних коливань і виключенні невідомого значення модуля крутіння f з використанням пробного (еталонного) тіла з відомим моментом інерції. Період коливань вимірюють двічі: а) для досліджуваного тіла, для якого період коливань маятника
б) для тіла, складеного з досліджуваного тіла з моментом інерції Jх і пробного (еталонного) тіла з моментом інерції J. якщо їх центри мас знаходяться на вісі обертання, період коливань складеного тіла визначається за формулою,
Звівши обидві частини виражень для періодів у квадрат і, поділивши одне на друге, одержимо пропорцію
з якої випливає
Момент інерції пробного (еталонного) тіла J, в якості якого, як правило, вибирають однорідне тіло провильної геометричної форми (куля, циліндричне кільце, куб, паралеліпіпед та інш.) тому, що його момент інерції можна розрахувати за формулою (1.4). На приклад, момент інерції циліндричного кільця відносно вісі, що співпадає з геометричною віссю, дорівнює
де R і r - відповідно зовнішній і внутрішній радіуси кільця, а d1 і d2 їхні діаметри, m ¾ маса кільця. Момент інерції суцільного однорідного циліндра масою m і радіуса R відносно вісі, що співпадає з геометричною віссю, дорівнює
Куля масою m і радіуса R має момент інерцї
Геометричні розміри пробного тіла вимірюють штангенциркулем, а масу знаходять зважуванням на вагах. Періоди коливань Т1 і Т2 досліджуваного й складного тіла визначають, вимірюючи час N =10¸20 коливань секундоміром (t1 і t2).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.120.103 (0.008 с.) |

 розкручує маятник на всю довжину нитки h1 і, проходячи, нижню точку, починає підніматися в гору. Після підняття тягарця на висоту h2<h1, маятник зупиняється й починає обертовий рух у протилежному напрямкові.
розкручує маятник на всю довжину нитки h1 і, проходячи, нижню точку, починає підніматися в гору. Після підняття тягарця на висоту h2<h1, маятник зупиняється й починає обертовий рух у протилежному напрямкові. ,
, де r ¾ радіус шківа. Запишемо рівняння руху тягарця та маятника, виходячи з наступного. При опусканні тягарця, маятник приводиться в обертовий рух моментом сили натягу
де r ¾ радіус шківа. Запишемо рівняння руху тягарця та маятника, виходячи з наступного. При опусканні тягарця, маятник приводиться в обертовий рух моментом сили натягу  , де
, де  ¾радіус-вектор точки прикладання сили відносно центра обертання, а момент сили тертя
¾радіус-вектор точки прикладання сили відносно центра обертання, а момент сили тертя  гальмує цей рух (див. Рис.1.3.). Вектор кутового прискорення
гальмує цей рух (див. Рис.1.3.). Вектор кутового прискорення  лежить на осі обертання і
лежить на осі обертання і 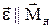 , причому
, причому  . Усі три вектори
. Усі три вектори  лежать на осі обертання і тому, вибравши напрям вектора кутового прискорення за додатній, векторне рівняння другого закону Ньютона для обертового руху маятника
лежать на осі обертання і тому, вибравши напрям вектора кутового прискорення за додатній, векторне рівняння другого закону Ньютона для обертового руху маятника
 .
. ¾ модуль моменту сили натягу підвісу. При опусканні тягарця, на нього діють прискорююча сила тяжіння
¾ модуль моменту сили натягу підвісу. При опусканні тягарця, на нього діють прискорююча сила тяжіння  та гальмуюча сила натягу
та гальмуюча сила натягу  , причому
, причому  . Вектор прискорення
. Вектор прискорення  . Усі три вектори лежать на одній прямій і тому, вибравши за додатній напрямок вектора прискорення, векторне рівняння другого закону Ньютона для прискореного руху тягарця
. Усі три вектори лежать на одній прямій і тому, вибравши за додатній напрямок вектора прискорення, векторне рівняння другого закону Ньютона для прискореного руху тягарця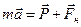
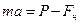 .
. . (2.3)
. (2.3) . (3.3)
. (3.3) . (4.3)
. (4.3) і знайдемо J:
і знайдемо J: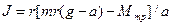 . (5.3)
. (5.3) , (6.3)
, (6.3)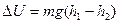 . Після підстановки в (6.3) значень кута повороту та енергії одержимо значення моменту сили тертя
. Після підстановки в (6.3) значень кута повороту та енергії одержимо значення моменту сили тертя . (7.3)
. (7.3) . (8.3)
. (8.3) (9.3)
(9.3) (10.3)
(10.3) - це різниця квадратів часу опускання тягарця з висоти h при наявності моменту сили опору рухові і часу його вільного падіння з тієї ж висоти. Очевидно, що час вільного падіння завжди менше часу руху при наявності супротиву при однаковому переміщенні, тому з достатньою надійністю можна вважати
- це різниця квадратів часу опускання тягарця з висоти h при наявності моменту сили опору рухові і часу його вільного падіння з тієї ж висоти. Очевидно, що час вільного падіння завжди менше часу руху при наявності супротиву при однаковому переміщенні, тому з достатньою надійністю можна вважати  >>
>>  . Прийнявши це зауваження із (10.3) отримаємо
. Прийнявши це зауваження із (10.3) отримаємо . (11.3)
. (11.3) . (12.3)
. (12.3)
 установка складається з платформи, на якій встановлені блок керування та індикації і стойка; перпендикулярно стойці закріплена вісь з електромагнітним гальмом, навколо котрої обертаються хрестовина із шківом і важками; на шків намотана нерозтяжна нитка, перекинута через блок, до якої приєднаний тягарець; у верхній та нижній частині стойки розташовані фотоелектричні датчики положення тягарця, відстань між якими визначається за шкалою, розташованою на боковій поверхні стойки. тягарець піднімається вгору шляхом намотування нитки на шків при обертанні хрестовини. При цьому робота зовнішніх сил по підняттю тягарця від положення датчика 2 до положення датчика 1 чисельно дорівнює потенційній енергії, що він отримує, якщо буде піднятий на висоту h, яка відраховується по шкалі на стійці.
установка складається з платформи, на якій встановлені блок керування та індикації і стойка; перпендикулярно стойці закріплена вісь з електромагнітним гальмом, навколо котрої обертаються хрестовина із шківом і важками; на шків намотана нерозтяжна нитка, перекинута через блок, до якої приєднаний тягарець; у верхній та нижній частині стойки розташовані фотоелектричні датчики положення тягарця, відстань між якими визначається за шкалою, розташованою на боковій поверхні стойки. тягарець піднімається вгору шляхом намотування нитки на шків при обертанні хрестовини. При цьому робота зовнішніх сил по підняттю тягарця від положення датчика 2 до положення датчика 1 чисельно дорівнює потенційній енергії, що він отримує, якщо буде піднятий на висоту h, яка відраховується по шкалі на стійці.
 . (13.3)
. (13.3) його руху, існує лінійна кореляція (відповідність), можна вважати справедливим основний закон обертового руху із заданою довірчою імовірністю (Рис.3.3).
його руху, існує лінійна кореляція (відповідність), можна вважати справедливим основний закон обертового руху із заданою довірчою імовірністю (Рис.3.3). Залежність величини моменту інерції маятника від розподілу мас відносно вісі обертання досліджується при різних положеннях пересувних важків m0, визначивши момент інерції за виразом (11.3), вимірюючи час руху тягарця при його незмінній масі, але при зміні відстані між пересувними важками R і віссю обертання. Відповідно до (8.3) між величиною моменту інерції J і R2 повинна бути лінійна кореляція (Рис.4.3).
Залежність величини моменту інерції маятника від розподілу мас відносно вісі обертання досліджується при різних положеннях пересувних важків m0, визначивши момент інерції за виразом (11.3), вимірюючи час руху тягарця при його незмінній масі, але при зміні відстані між пересувними важками R і віссю обертання. Відповідно до (8.3) між величиною моменту інерції J і R2 повинна бути лінійна кореляція (Рис.4.3).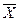

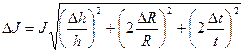 . (14.3)
. (14.3)
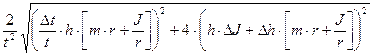 . (15.3)
. (15.3) .
. .
. і розглянути їх як точкові. При цьому момент інерції тіла дорівнює сумі моментів інерції його складових
і розглянути їх як точкові. При цьому момент інерції тіла дорівнює сумі моментів інерції його складових або для однорідного тіла
або для однорідного тіла  . (1.4)
. (1.4) Крутильний маятник ¾ макроскопічне тіло з моментом інерції J, закріплене нерухомо на пружному стержні (Рис.1.4). Коливання визначаються кутом відхилення
Крутильний маятник ¾ макроскопічне тіло з моментом інерції J, закріплене нерухомо на пружному стержні (Рис.1.4). Коливання визначаються кутом відхилення  тіла від положення рівноваги, вектором кутової швидкості
тіла від положення рівноваги, вектором кутової швидкості  та вектором кутового прискорення
та вектором кутового прискорення  . Тіло здійснює малі періодичні коливання під дією моменту
. Тіло здійснює малі періодичні коливання під дією моменту  зовнішньої сили
зовнішньої сили  , моменту
, моменту  сили опору
сили опору  та моменту
та моменту  пружної сили деформації кручення
пружної сили деформації кручення  . Кефіцієнт f називається модулем кручення. Лінійна залежність моменту сил кручення від кута повороту виконується лише для малих коливань.
. Кефіцієнт f називається модулем кручення. Лінійна залежність моменту сил кручення від кута повороту виконується лише для малих коливань. . (2.4)
. (2.4) лежать на одній прямій, а тому, взявши напрямок кутового прискорення
лежать на одній прямій, а тому, взявши напрямок кутового прискорення  за додатній, векторне рівняння (2.4) можна записати в алгебраїчній формі:
за додатній, векторне рівняння (2.4) можна записати в алгебраїчній формі: ,
, , (3.4)
, (3.4) ¾ коефіцієнт згасання коливань,
¾ коефіцієнт згасання коливань,  , w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника
, w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника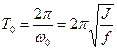 . (4.4)
. (4.4) ,
, .
.
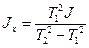 . (5.4)
. (5.4) , (6.4)
, (6.4) . (7.4)
. (7.4)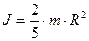 . (8.4)
. (8.4)


