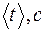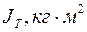Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення моменту інерції тіл різної форми методом крутильних коливань трифілярного підвісуСодержание книги
Поиск на нашем сайте
Мета лабораторної роботи: Визначення моменту інерції твердих тіл різної форми методом крутильних коливань трифілярного підвісу.
Деякі теоретичні положення Момент інерції тіла довільної форми можна виміряти методом трифілярного підвісу. Трифілярний підвіс складається з круглої плоскої платформи D у вигляді диска та малого диска H, які з’єднані трьома металевими нитками або дротами. Нитки однакової довжини закріплені симетрично по вершинах рівнобічного трикутника та рівномірно навантажені вагою платформи D. Диск меншого діаметра H закріплений в горизонтальному положенні до спеціального контейнера, вмонтованого в стіну так, що платформа D звисає на нитках над підлогою на висоті 1,5 м. Платформа D може здійснювати крутильні коливання навколо вертикальної вісі, яка перпендикулярна до її площини і проходить через її центр мас. За допомогою крутильних коливань платформи D можна визначити момент інерції цієї платформи, а також момент інерції будь якого тіла, розміщеного на ній. Тіло на платформу поміщують таким чином, щоб рівномірний натяг ниток не порушувався (рис.1). Позначимо довжину ниток через l, а відстані від точок їх закріплення до центрів платформи D та диска H відповідно через R та r. При повороті платформи на деякий кут α0 відносно верхнього диска внаслідок крутильних коливань точка закріплення нитки А переміщується в положення А1, а центр мас платформи переміщується вздовж вісі обертання набуваючи найвищого положення при максимальному відхиленні платформи від положення рівноваги та найнижчого при положенні рівноваги. Максимальну висоту, на яку піднімається центр мас платформи, можна визначити із співвідношення
Цей вираз можна записати у вигляді
Із геометричних даних маємо
На основі цих рівнянь вираз для h можна привести до такого вигляду
При великій довжині нитки та малих кутах відхилення платформи в цьому виразі значення ВС та ВС1 можна вважати рівними l, а значення синуса кута α0 замінити просто значенням α0. Таким чином остаточно маємо
На основі цього виразу, для потенціальної енергії платформи, при її відхиленні від положення рівноваги на кут α 0, отримуємо
де m – маса платформи D. Кінетична енергія обертального руху Ек платформи при проходженні нею положення рівноваги на визначається за формулою
де J – момент інерції платформи відносно вертикальної осі, яка проходить через центр мас платформи, а Визначимо значення кутової швидкості платформи D в цей момент, вважаючи що коливання платформи відбуваються за гармонічним законом. У цьому випадку залежність зміщення платформи від часу можна записати у такому вигляді
де α – кутове зміщення в момент часу t; α0 – кутова амплітуда; Т – період обертання. Кутова швидкість
При проходженні тілом положення рівноваги (t = 0, Т/2, Т, 3Т/2...)
Враховуючи формулу (10) вираз (7) можна записати так
Нехтуючи силами тертя з рівнянь (6) та (11) на основі закону збереження енергії маємо
З формули (12) одержимо робочу формулу для визначення моменту інерції платформи відносно вертикальної осі, яка проходить через її центр мас:
Усі величини в правій частині цієї формули доступні для безпосереднього вимірювання. Якщо на платформу помістити досліджуване тіло, маса якого повинна бути попередньо визначена і знову виміряти період коливань навантаженої платформи, то можна визначити момент інерції тіла відносно вертикальної осі, яка проходить через центр мас цього тіла і центр мас платформи. Так як згідно з адитивністю моменту інерції момент інерції системи тіл є сумою моментів інерції ненавантаженої платформи Jпл та розташованого на ній тіла, то момент інерції тіла JT
Порядок виконання роботи.
1. Виміряйте лінійні розміри платформи і досліджуваних тіл, які необхідні для розрахунку їх маси. За даними щодо об’єму тіл і густини сталі 2. Проведіть під керівництвом інженера практикуму тренувальні вправи щодо оволодіння методикою збудження малих крутильних коливань платформи, під час яких амплітуда коливань не може бути більшою ніж 6- 8◦. 3. Визначте середній період коливань пустої платформи 4. Виміряйте величини l, R, та r. За формулою (13) обчисліть момент інерції пустої платформи Jпл. 5. Покладіть на платформу одне з досліджуваних тіл, момент інерції якого треба визначити. Тіло на платформу треба класти строго симетрично, щоб не було перекосу платформи, тобто так, щоб вісь обертання проходила через центр мас тіла. Для цього платформа має вертикальну шпильку, яка входить у відповідний отвір в досліджуваному тілі при його поміщенні на платформу. 6. Спричинивши малі крутильні коливання платформи D треба не менше ніж 5 разів виміряти секундоміром тривалість 40-50 повних малих коливань платформи з досліджуваним тілом. Обчисліть середнє значення тривалості вибраного вами для досліджень числа повних малих коливань 7. За методикою, описаною у п.6, визначте середні періоди коливань платформи, які вона здійснює разом з поміщеним на неї кожним із досліджуваних тіл. Для обох циліндричних тіл період коливань треба визначити при двох їх положеннях щодо платформи: при вертикальному (паралельному осі обертання) та при горизонтальному (перпендикулярному до вісі обертання). 8. З результатів вимірювань за формулою (13) розрахуйте моменти інерції платформи J, навантаженої кожним з досліджуваних тіл. При обчисленні J – моменту інерції навантаженої платформи маса системи визначається як сума мас платформи та тіла. 9. За формулою (14) визначте моменти інерції досліджених тіл. Дані вимірювань і розрахунків запишіть у таблицю №1. 10. Виведіть формулу для обчислення абсолютної та відносної похибок і визначте їх для моменту інерції ненавантаженої платформи. 11. Проведіть за формулою для визначення моменту інерції циліндра відносно вісі обертання, яка проходить через його центр мас, теоретичний розрахунок моменту інерції циліндра, дослідженого в лабораторній роботі. Порівняйте результати розрахунку із даними щодо його моменту інерції, отриманими з експерименту. Таблиця №1
Література: [1-15,17,19,25-38] Лабораторна робота №8
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 Якщо платформу D повернути на невеликий кут відносно вертикальної вісі, яка проходить через її центр мас, то всі три нитки набудуть похиле положення; внаслідок чого центр мас платформи піднімається. Після цього платформа може здійснювати обертальні коливання навколо вертикальної вісі, яка проходить через її центр. Період коливань платформи визначається величиною її моменту інерції. Він буде іншим, якщо платформу додатково навантажити будь-яким тілом.
Якщо платформу D повернути на невеликий кут відносно вертикальної вісі, яка проходить через її центр мас, то всі три нитки набудуть похиле положення; внаслідок чого центр мас платформи піднімається. Після цього платформа може здійснювати обертальні коливання навколо вертикальної вісі, яка проходить через її центр. Період коливань платформи визначається величиною її моменту інерції. Він буде іншим, якщо платформу додатково навантажити будь-яким тілом. . (1)
. (1) . (2)
. (2) ,
, . (3)
. (3) . (4)
. (4) . (5)
. (5)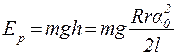 , (6)
, (6) , (7)
, (7)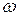 - кутова швидкість платформи у момент досягнення нею положення рівноваги.
- кутова швидкість платформи у момент досягнення нею положення рівноваги. , (8)
, (8) . (9)
. (9) , тому
, тому  . (10)
. (10) . (11)
. (11) . (12)
. (12)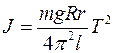 . (13)
. (13) . (14)
. (14) , з якої вони виготовлені, розрахуйте маси досліджуваних тіл.
, з якої вони виготовлені, розрахуйте маси досліджуваних тіл. . Для цього спричинивши малі крутильні коливання платформи D треба не менше ніж 5 разів виміряти секундоміром тривалість 40-50 повних малих коливань пустої платформи. Обчисліть середнє значення тривалості вибраного вами для досліджень числа повних малих коливань
. Для цього спричинивши малі крутильні коливання платформи D треба не менше ніж 5 разів виміряти секундоміром тривалість 40-50 повних малих коливань пустої платформи. Обчисліть середнє значення тривалості вибраного вами для досліджень числа повних малих коливань  і середнє значення періоду коливань пустої платформи
і середнє значення періоду коливань пустої платформи  .
.