
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вивчення коливань зв’язаних маятниківСодержание книги
Поиск на нашем сайте
Мета лабораторної роботи: Вивчення особливостей коливань зв’язаної системи.
Як відомо, коливанням називається всякий рух або зміна стану тіла (коливальної системи), що характеризується тим чи іншим ступенем повторюваності в часі значень фізичних величин, які визначають цей рух або стан тіла. Вільні коливання коливальної системи відбуваються після того, як вона була виведена із стану рівноваги і залишена сама на себе. Власні коливання системи здійснюються за рахунок енергії, яка була надана системі і відбуваються за відсутності дії в цій системі сил опору, а також за відсутності дії на неї інших зовнішніх впливів. Коливання називаються періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Найпростішим типом періодичних коливань є так звані гармонічні коливання, при яких значення фізичної величини змінюються у часі за законом косинуса (синуса). Якщо абсолютно тверде тіло (фізичний маятник) здійснює малі власні вільні гармонічні коливання, то його період коливань
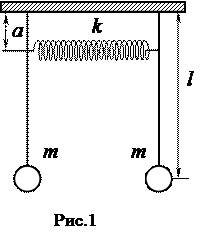
Кожне з двох твердих тіл, зв’язаних одне з одним динамічним зв’язком, які утворюють, так звану зв’язану систему, буде коливатися з двома різними частотами. Властивості будь якої зв’язаної системи визначаються властивостями двох вихідних коливальних систем, які утворюють цю зв’язану систему. Якщо різниця частот коливань мала, то будуть спостерігатися биття, тобто періодична зміна (збільшення і зменшення) амплітуди коливань. Два математичних маятники, з’єднані між собою пружиною, є найпростішим прикладом зв’язаної системи. Маятники мають однакові власні частоти коливань, доки коливаються незалежно один від одного. Частота довільних коливань маятника за наявності зв’язку відрізняється від його власної частоти, оскільки при коливанні маятників пружина деформується і, значить, змінюється сила, яка діє на маятники. При відхиленні одного з маятників з положення рівноваги за наявності динамічного зв’язку між маятниками буде відхилятись і другий маятник. Розглянемо на якісному рівні особливості коливання двох однакових маятників, зв’язаних пружиною (рис.1). Відхилимо подумки один з них (правий) на певний кут від положення рівноваги так, щоб пружина здеформувалась. Лівий маятник при цьому повинен перебувати у стані спокою. Потім правий маятник відпустимо. Він почне коливатись навколо положення рівноваги. Спочатку правий маятник гойдається так, ніби ніякого зв’язку з лівим він не має. Поступово лівий маятник також почне розгойдуватися, оскільки між маятниками почне здійснюватись обмін коливальною енергією. Так як енергія від правого маятника, буде поетапно передаватися лівому маятнику, то з часом амплітуда коливань правого маятника буде поступово зменшуватись, в той час як амплітуда коливань лівого маятника буде зростати. Все це буде тривати деякий час Тб/2 доти, доки правий маятник не зупиниться. При цьому лівий маятник (якщо втрати на тертя малі) буде коливатись майже з такою ж амплітудою, яка була у правого маятника спочатку. Потім маятники знову поступово «обмінюються ролями»: лівий маятник буде розгойдувати правий, а тому процес обміну коливальною енергією повністю повториться, так як маятники однакові. Таким чином обидва маятники, з’єднані між собою пружиною, будуть здійснювати коливання, амплітуди яких увесь час, то збільшуються, то зменшуються. Як відомо, такі коливання називаються биттями, а час Тб – періодом биття. За час Тб/2 маятники будуть обмінюватись коливальною енергією. Механічна енергія буде весь час переходити від одного маятника до іншого до того часу, доки вона не перетвориться в теплову, у результаті чого обидва маятники зупиняться. Якщо якимось чином спочатку довільно відхилити обидва маятника від положення рівноваги, а потім відпусти їх, то знову амплітуда коливань першого маятника не буде залишатися постійною: вона буде то збільшуватися, то зменшуватися. Відповідним чином буде відбуватись і зміна амплітуди коливань другого маятника. Якщо в ході коливання досліджуваної зв’язаної системи амплітуда коливань першого маятника збільшується, то у другого вона обов’язково зменшується. Однак тепер амплітуда змінюється від деякого максимуму до деякого мінімуму; час „перекачування” енергії все рівно дорівнює Тб/2. Як би не збуджувалися коливання обох маятників, завжди період биттів буде однаковим. У залежності від способу збудження коливань змінюється лише різниця між максимумом та мінімумом амплітуди коливань маятників. Коливання кожного за маятників, взагалі кажучи, у цьому випадку не є гармонічними. Кожний маятник здійснює як би гармонічне коливання, але амплітуда його пульсує (періодично змінюється з однаковим періодом биття Тб). На практиці можна застосувати два способи збудження гармонічних коливань у обох зв’язаних маятників. Перший з них такий – обидва маятника треба відхилити на малий кут Таким чином, власні коливання двох зв’язаних маятників можуть бути представлені як результат додавання (накладання, суперпозиції) двох гармонічних коливань, які здійснюються з різними циклічними частотами ω1 та ω2. Частоти ω1 та ω2 залежать від фізичних параметрів маятників: їх довжини l, маси m, коефіцієнта жорсткості пружини k, відстані від місця її закріплення до вісі обертання маятника а. Встановлено, що між цими параметрами існує така залежність
Циклічні частоти ω1 та ω2 називають власними або нормальними частотами нормальних коливань зв’язаної системи. Гармонічні коливання, які зв’язана система здійснює після відхилення маятників у фазі, є власними коливаннями маятників з меншою нормальною частотою ω1. Власні коливання з більшою нормальною циклічною частотою ω2 спостерігаються при відхилення обох маятників в протифазі. Отже, власні коливання з меншою нормальною циклічною частотою є синфазними гармонічними коливаннями обох маятників, а власні коливання з більшою нормальною частотою є протифазними гармонічними коливаннями обох маятників. Для того щоб проаналізувати процес виникнення биттів, розглянемо задачу про додавання двох гармонічних коливань, які здійснюються з близькими частотами. Як відомо, додавання двох гармонічних коливань з однаковими частотами та одного напрямку дає гармонічне коливання тієї самої частоти. Коливання, отримане в результаті додавання двох гармонічних коливань, які мають один напрямок, але різні циклічні частоти, не є гармонічним коливанням. Нехай
Результуюче, сумарне коливання
Перший член рівняння (4) не є гармонічним коливанням, так як він є добутком двох гармонічних множників, перший з яких має частоту (ω1–ω2)/2, а другий – частоту (ω1+ω2)/2. Якщо частоти ω1 та ω2 не дуже відрізняються одна від одної, то частота (ω1+ω2)/2 приблизно одного порядку з ω1 (або ω2), але частота (ω1–ω2)/2 буде порівняно з ω1 (або ω2) дуже малою. У цьому випадку перший член рівняння (4), яке описує результуючий рух маятників можна розглядати як періодичне коливання з пульсуючою амплітудою, тобто биття двох близьких частот, яке здійснюється з періодом
У цього коливання амплітуда Аб (амплітуда биттів) повільно (по відношенню до
У зв’язку з тим, що період модуля косинуса дорівнює
Рис.2
Графік таких коливань представлено на рис.2. Їх називають биттями двох близьких частот, або так званими «чистими биттями». Другий член виразу (4) описує гармонічне коливання, яке здійснюється з частотою ω2. Додавання «чистих биттів» з цим гармонічними коливаннями, як показують експериментальні дослідження, дає картину биттів, при яких амплітуда коливань змінюється з періодом биттів Тб, але ніколи не досягає нуля. При додаванні двох коливань з однаковою амплітудою А = В биття будуть чистими, а при А ≠ В отримаємо звичайні биття двох близьких частот, причому їх частота ωб=2π/Тб із врахуванням формули (7) дорівнює:
Частота биттів дорівнює модулю різниці нормальних циклічних частот гармонічних коливань, з яких вони утворені. Вона не залежить від їх амплітуд та початкових фаз. Проаналізувавши дані щодо власних коливань маятників, які утворюють зв’язану систему, і врахувавши результати теоретичного аналізу додавання двох гармонічних коливань різних частот, приходимо до висновку про те, що власні коливання двох маятників, з’єднаних пружиною, є суперпозицією двох гармонічних коливань, причому різниця нормальних частот цих коливань дорівнює частоті биттів. Теоретичним аналізом та експериментальними дослідженнями встановлено, що при коливальному русі зв’язаної системи виконуються такі закономірності:
Опис експериментальної установки та методики вимірювань.
Установка складається з рами, на якій підвішені два однакових металеві маятники. Маятники складаються з довгих легких титанових стрижнів, на нижньому кінці яких закріплені стальні циліндри маси m. Верхні кінці стрижнів закріплені у внутрішні шайби підшипників, зовнішні шайби яких закріплені на рамі таким чином, щоб площина підшипників, а значить, і площина руху маятників співпадала з площиною рами. На різних висотах ai від точки підвісу (центра підшипника) на стрижнях симетрично поміщені муфточки з отворами, які служать для закріплення легкої пружини зв’язку. Довжина цієї пружини в не розтягнутому стані точно дорівнює відстані між стрижнями маятників у не відхиленому положенні. Установка укомплектована спеціальним пристроєм для визначення коефіцієнта жорсткості пружини k статичним методом, який складається із закріпленої вертикально на штативі лінійки з міліметровою шкалою і набору різних важків з відомою масою. Маса маятника m, ефективна довжина маятника l (відстань від точки підвісу до центра циліндра) і відстані ai від точок закріплення пружини до центра підвісу відомі. Вони вказані на установці.
Порядок виконання роботи.
1. Визначте періоди власних малих коливань кожного з маятників Т0. Для цього треба за допомогою секундоміра не менше ніж 3 рази визначити час, впродовж якого здійснюється 50 повних малих коливань кожного з маятників, які не з’єднані пружиною. Обчисліть середній період власних коливань 2. Встановіть пружину зв’язку на вказаній керівником занять відстані від точки підвісу aі приступіть до вимірювання частот коливань зв’язаних маятників. Усі вимірювання треба здійснювати не менше ніж три рази і визначати середні арифметичні значення одержаних величин. 3. Визначте період Т1 малих коливань маятників в фазі. Для цього треба, користуючись для відліку мітками, які є на установці, відхилити обидва маятники в одну сторону на малий кут
обчисліть середню першу нормальну циклічну частоту коливань 4. Визначте період Т2 малих коливань маятників у протифазі. Для цього треба, користуючись для відліку мітками, які є на установці, відхилити обидва маятники на малий кут
обчисліть середню другу нормальну циклічну частоту коливань 5. Визначте період биттів Тб. Для збудження коливань з биттями правий маятник треба відхилити від положення рівноваги так, щоб пружина зв’язку в процесі коливань увесь час залишилась у натягнутому стані. При такому способі збудження початкове зміщення лівого маятника не буде у точності дорівнювати нулю, але воно буде малим. Після збудження коливань з биттями треба виміряти час між трьома послідовними зупинками в русі лівого маятника. За даними дослідів обчисліть середнє значення періоду биттів 6. Визначте період періодичних коливань маятників при биттях 7. За отриманими експериментальними даними щодо визначених середніх значень обох циклічних нормальних частот, а також циклічної частоти биттів та циклічної частоти періодичних коливань маятників при биттях перевірте виконання (в межах похибки експерименту) таких співвідношень:
8. З метою перевірки збігу результатів, отриманих з використанням різних методик вимірювань, описаних у лабораторій роботі, розрахуйте і порівняйте між собою абсолютні похибки, з якими у роботі визначені фізичні величини, що входять у праві та у ліві частини рівнянь (12). Зробіть висновки щодо одержаних результатів. Література: [3-6,7,11,20-35] Лабораторна робота №7
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.141 (0.009 с.) |

 Деякі теоретичні відомості
Деякі теоретичні відомості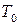 не залежить від амплітуди коливань (ізохронність маятника). При цьому тіло коливається з власною частотою коливань
не залежить від амплітуди коливань (ізохронність маятника). При цьому тіло коливається з власною частотою коливань 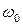 , яка визначається параметрами даної коливальної системи і дорівнює
, яка визначається параметрами даної коливальної системи і дорівнює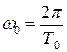 . (1)
. (1)
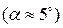 однаково в одну сторону від положення рівноваги, а потім одночасно відпустити. Другий спосіб збудження є таким – обидва маятника треба відхилити на такий же малий кут в різні сторони від положення рівноваги, а потім одночасно відпустити. Після збудження коливань за першим способом обидва маятника будуть здійснювати коливання так, ніби пружини, яка їх з’єднує, немає, оскільки у цьому випадку пружина зв’язку не розтягується і не впливає на рух кожного маятника. Якщо пружина має малу вагу, то обидва маятники синхронно (синфазно) коливаються з таким же самим періодом коливань Т1, з яким здійснював би власні коливання кожний з них за відсутності зв’язку між ними. Після збудження коливань другим способом маятники будуть здійснювати протифазні коливання. Обидва маятника перебувають за однакових умов і здійснюють гармонічні коливання з періодом Т2. Період коливань Т2 буде меншим за період коливань, так як у другому випадку до «вертаючої» сили маятника додається ще і «вертаюча» сила пружини.
однаково в одну сторону від положення рівноваги, а потім одночасно відпустити. Другий спосіб збудження є таким – обидва маятника треба відхилити на такий же малий кут в різні сторони від положення рівноваги, а потім одночасно відпустити. Після збудження коливань за першим способом обидва маятника будуть здійснювати коливання так, ніби пружини, яка їх з’єднує, немає, оскільки у цьому випадку пружина зв’язку не розтягується і не впливає на рух кожного маятника. Якщо пружина має малу вагу, то обидва маятники синхронно (синфазно) коливаються з таким же самим періодом коливань Т1, з яким здійснював би власні коливання кожний з них за відсутності зв’язку між ними. Після збудження коливань другим способом маятники будуть здійснювати протифазні коливання. Обидва маятника перебувають за однакових умов і здійснюють гармонічні коливання з періодом Т2. Період коливань Т2 буде меншим за період коливань, так як у другому випадку до «вертаючої» сили маятника додається ще і «вертаюча» сила пружини.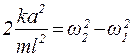 . (2)
. (2)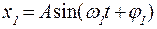 ;
; 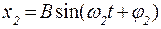 . (3)
. (3)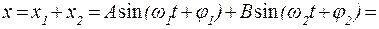
 . (4)
. (4)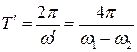 . (5)
. (5)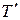 ) змінюється з часом від 0 до 2А за законом косинуса
) змінюється з часом від 0 до 2А за законом косинуса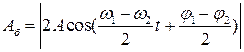 . (6)
. (6)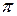 , період зміни амплітуди (період биттів)
, період зміни амплітуди (період биттів)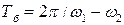 . (7)
. (7)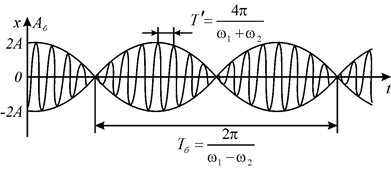
 . (8)
. (8)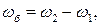
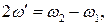
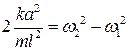 . (9)
. (9)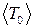 і середню власну частоту коливань кожного з маятників
і середню власну частоту коливань кожного з маятників 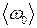 .Пересвідчіться у тому, що частоти власних коливань обох маятників співпадають.
.Пересвідчіться у тому, що частоти власних коливань обох маятників співпадають.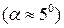 від положення рівноваги. Спричинивши рух обох маятників виміряйте, користуючись секундоміром, час, впродовж якого лівий маятник здійснює 50 повних малих коливань у фазі. Обчисліть середнє значення періоду коливань у фазі
від положення рівноваги. Спричинивши рух обох маятників виміряйте, користуючись секундоміром, час, впродовж якого лівий маятник здійснює 50 повних малих коливань у фазі. Обчисліть середнє значення періоду коливань у фазі 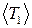 . За формулою
. За формулою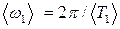 (10)
(10)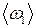 . Якщо пружина зв’язку в процесі визначення періоду коливань маятників у фазі не розтягувалась, а значить не впливала на рух маятників, то у цьому випадку обидва маятники повинні були коливатись з першою нормальною частотою, яка в межах похибки повинна дорівнювати частоті власних коливань маятників. Порівняйте одержане значення
. Якщо пружина зв’язку в процесі визначення періоду коливань маятників у фазі не розтягувалась, а значить не впливала на рух маятників, то у цьому випадку обидва маятники повинні були коливатись з першою нормальною частотою, яка в межах похибки повинна дорівнювати частоті власних коливань маятників. Порівняйте одержане значення 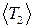 . За формулою
. За формулою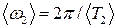 (11)
(11)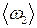 .
.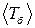 та середню циклічну частоту биттів
та середню циклічну частоту биттів 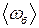 .
.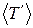 та середню циклічну частоту при биттях
та середню циклічну частоту при биттях 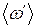 .
.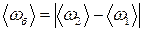 ,
, 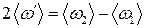 ,
, 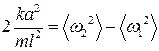 . (12)
. (12)


