
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Похибки вимірювань фізичних величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Класифікація вимірювань
Наукове спостереження полягає в цілеспрямованому і планомірному сприйнятті властивостей предметів і явищ дійсності для одержання відповідної інформації про об’єкт пізнання за допомогою органів чуття. У здійсненні наукового спостереження значну роль відіграє теоретичне мислення. Дослідник не просто реєструє факти. Він свідомо відшукує їх, користуючись певною ідеєю, гіпотезою тощо. Результати наукових спостережень відповідно інтерпретуються на основі певної теорії. У наукових спостереженнях широко використовують спеціальні засоби і прилади, які компенсують природну обмеженість органів чуттів людини, підвищують точність і об’єктивність результатів спостереження. Експеримент ґрунтується на забезпеченні відтворення явища в лабораторній обстановці і супроводжується точними, по можливості, вимірюваннями та математичною обробкою даних. За структурою експеримент суттєво відрізняється від спостереження наявністю спеціальних матеріальних засобів (експериментальних установок і приладів) впливу на досліджувані об’єкти або процеси. Вимірювання фізичних величин є метою кожної лабораторної роботи. Вимірювання – це порівняння способом фізичного експерименту даної фізичної величини з відомою однорідною величиною, взятою за одиницю вимірювання. У результаті встановлюється, у скільки разів вимірювана величина більша або менша від одиниці вимірювання. За способом знаходження результату вимірювання поділяють на два основні види: прямі і непрямі. Прямі вимірювання – це такі вимірювання, в яких шукане значення величини знаходять безпосередньо з досліду, порівнюючи його з мірою цієї величини за даними відліку, здійсненого за допомогою відлікового пристрою вимірювального приладу. Відліком у метрології прийнято називати число, відраховане по відліковому пристрою засобу вимірювання. Прикладом найпростіших прямих вимірювань може бути вимірювання довжини масштабною лінійкою, сили струму – амперметром, проміжків часу – секундоміром та ін. Непрямі вимірювання – це такі вимірювання, результат яких розраховують за відомою функціональною залежністю, вираженою аналітичною формулою, з використанням даних, одержаних в результаті проведення прямих вимірювань. Наприклад, об'єм прямокутного паралелепіпеда може бути знайдений за формулою
Похибки прямих вимірювань
При будь-якому вимірюванні фізичної величини, як би старанно його не проводили, неминучі похибки, тобто виміряти величину абсолютно точно неможна. Вимірювання фізичної величини не може бути проведене з абсолютною точністю з цілого ряду причин, таких як недоліки приладів, методів вимірювання, впливу зовнішніх умов, індивідуальних властивостей спостерігача та ін. Тому метою вимірювання є не тільки відшукання наближеного значення величини, а й оцінювання його відхилення від істинного значення. Обов'язково потрібно вказувати точність, гарантовану даним вимірюванням, або його похибку. Розрізняють абсолютні та відносні похибки. Похибку, виражену різницею між виміряним
Але істинне значення фізичної величини нам невідоме, тому можна знайти тільки наближену похибку, при цьому замість істинного значення величини беруть найбільш ймовірне її значення, яке за великої кількості вимірювань дорівнює середньому арифметичному всіх виміряних значень. Виміряне значення Якість результатів вимірювання краще характеризує відносна похибка. Відносну похибку визначають відношенням абсолютної похибки до дійсного (середнього арифметичного) значення величини. Цю похибку виражають у процентах (відсотках):
Відносна похибка дозволяє зробити висновки про точність проведених вимірювань. У технічній літературі часто зустрічається поняття «точність вимірювань». Під цим розуміють величину, обернену до відносної похибки вимірювань без процентів. Так, якщо Вимірювання залежно від методу, приладів та властивостей об’єкта дослідження можуть бути з одноразовими або багаторазовими спостереженнями. Відповідно перші називають звичайними вимірюваннями, а другі – статистичними вимірюваннями. Похибки вимірювань за характером і причинами їх появи поділяють на три класи: систематичні, випадкові та промахи. Систематична похибка – це та частина загальної похибки вимірювання, яка залишається сталою або змінюється закономірно при повторних вимірюваннях тієї самої величини. Систематична похибка має знак і викликає відхилення результату завжди в один бік. Через це дослідник, частіше за все, просто не підозрює про існування такої похибки. Причини виникнення систематичної похибки такі: неправильне градуювання приладу або його несправність; неправильне встановлення приладу та погані умови його роботи; невдалий вибір методу дослідження і т. д. Виявлення, оцінювання та позбавлення від систематичних похибок є головними завданнями дослідника. Для цього необхідно ретельно готуватись до проведення вимірювання і продумувати методику його проведення. Наведемо деякі приклади. Якщо шкала приладу зміщена, то всі вимірювання матимуть сталу похибку, що дорівнює величині зміщення. Або коли металевою лінійкою вимірювати розміри тіла безпосередньо в нагрівальній печі. Внаслідок термічного розширення лінійки при її нагрівання збільшиться відстань між поділками лінійки і систематична похибка дорівнюватиме величині цього збільшення. В обох прикладах систематична похибка може бути виявлена. Несправний прилад можна порівняти з іншим аналогічним приладом, а температурну похибку можна розрахувати за температурним коефіцієнтом матеріалу лінійки. Але це зовсім не означає, що завжди можна повністю позбавитися систематичної похибки. Завжди існує власна похибка навіть у справного приладу, зумовлена недоліками його виготовлення. Таку похибку називають інструментальною похибкою. Поділки на шкалі приладу роблять відповідно до його інструментальної похибки. Масштабну лінійку градуюють через Аналогічну ситуацію маємо при зважуванні тіла за допомогою гир. У паспорті вказується, що гиря масою
За відсутності вказівок щодо похибки вимірювального приладу його абсолютну похибку беруть такою, що дорівнює половині ціни найменшої поділки його шкали. Випадкова похибка. З досвіду відомо, що багаторазові вимірювання тієї самої величини, проведені найточнішими приладами, дають значення, які дещо відрізняються одне від одного. У такому випадку має місце випадкова похибка, складова загальної похибки, що змінюється довільним чином при повторних вимірюваннях однієї величини. Поява випадкових похибок зумовлена конструкцією приладу (тертя між деталями та ін.), зміною зовнішніх умов (коливання температури, вібрації та ін.), а також суб’єктивним впливом на процес вимірювання самого спостерігача. Неможливо позбавитися випадкових похибок, але ми можемо зменшити їх вплив на кінцевий результат, використовуючи методи математичної статистики, що дозволяють визначити, яке зі значень найближче до істинного, та знайти похибку цього значення. Теорія похибок установлює що: 1.При багатократному вимірюванні однієї і тієї самої величини однакова ймовірність одержання значень як більших за істинне, так і менших, тому найближчим до істинного значення буде середнє арифметичне значення
де Значення 2.Результати окремих вимірювань відрізняються від
Ця різниця наближена до абсолютної похибки окремого вимірювання і є випадковою величиною. Середнє значення відхилення від середнього арифметичного, яке за своєю величиною близьке за величиною до середнього значення абсолютної похибки кількох вимірювань, знаходять за формулою:
Промахи. Про те, що під час проведення вимірювань були допущені грубі похибки (промахи), дізнаються здебільшого наприкінці досліджень, коли дістануть явно неправильні результати. Таким чином, можемо визначити промах як похибку, що суттєво перевищує очікувану за даних умов. Джерелом такої похибки може бути неуважність або помилка експериментатора, а також несправність засобу вимірювання. Якщо у результаті аналізу даних, одержаних під час проведення вимірювань, дослідник дійшов висновку, що результати вимірювань містять промахи, то ці, завідомо неправильні дані слід беззастережно відкинути. Після чого бажано встановити причину помилки, виправити несправності та недоліки і повторити вимірювання заново.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1014; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.013 с.) |

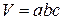 , де
, де  – ребра паралелепіпеда, довжина яких виміряна шляхом проведення прямих вимірювань за допомогою штангенциркуля або лінійки.
– ребра паралелепіпеда, довжина яких виміряна шляхом проведення прямих вимірювань за допомогою штангенциркуля або лінійки. і істинним
і істинним 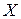 значеннями величини, називають абсолютною похибкою вимірювання. Вона визначається за формулою
значеннями величини, називають абсолютною похибкою вимірювання. Вона визначається за формулою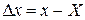 . (1)
. (1)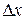 може бути як додатною, так і від'ємною, Але абсолютна похибка не дає повного уявлення про точність вимірювання, оскільки її величина не порівнюється із самою виміряною величиною.
може бути як додатною, так і від'ємною, Але абсолютна похибка не дає повного уявлення про точність вимірювання, оскільки її величина не порівнюється із самою виміряною величиною.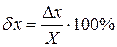 . (2)
. (2) , то точність таких вимірювань дорівнюватиме 100.
, то точність таких вимірювань дорівнюватиме 100. , а мікрометр має поділки, найменша ціна яких дорівнює одній сотій міліметра. На перший погляд здається, що за допомогою лупи можна провести підрахунок десятих, а то й сотих часток міліметра і на лінійці. Але це не так. Товщина самих поділок уже дає десяту частку міліметра, і нанесені вони з деякою похибкою, тому при вимірюванні лінійкою можна гарантувати мінімальну похибку, яка дорівнює ціні поділки, або
, а мікрометр має поділки, найменша ціна яких дорівнює одній сотій міліметра. На перший погляд здається, що за допомогою лупи можна провести підрахунок десятих, а то й сотих часток міліметра і на лінійці. Але це не так. Товщина самих поділок уже дає десяту частку міліметра, і нанесені вони з деякою похибкою, тому при вимірюванні лінійкою можна гарантувати мінімальну похибку, яка дорівнює ціні поділки, або  має інструментальну абсолютну похибку
має інструментальну абсолютну похибку  Таку похибку дають усій партії гир, порівнюючи вибірково деякі з них з еталоном. При цьому в жодному випадку похибка не перевищує
Таку похибку дають усій партії гир, порівнюючи вибірково деякі з них з еталоном. При цьому в жодному випадку похибка не перевищує 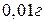 , але може бути меншою. Та нам це невідомо, тому маси тіл, виміряні за допомогою такої гирі,
, але може бути меншою. Та нам це невідомо, тому маси тіл, виміряні за допомогою такої гирі,  повинні мати похибку
повинні мати похибку  У цьому випадку інструментальна похибка є систематичною і тому при повторних вимірюваннях завжди дає відхилення виміряної величини від істинного значення в один бік, але невідомо в який. Отже, похибка подається з подвійним знаком і результат зважування запишеться так:
У цьому випадку інструментальна похибка є систематичною і тому при повторних вимірюваннях завжди дає відхилення виміряної величини від істинного значення в один бік, але невідомо в який. Отже, похибка подається з подвійним знаком і результат зважування запишеться так: .
. ряду окремих вимірювань
ряду окремих вимірювань 
 , (3)
, (3)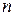 кількість вимірювань.
кількість вимірювань.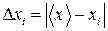 . (4)
. (4)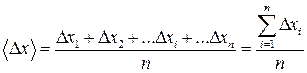 . (5)
. (5)


