
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення модуля Юнга сталі за методом деформації згинуСодержание книги
Поиск на нашем сайте
Мета лабораторної роботи Дослідження пружних властивостей стрижня при його згинанні. Визначення модуля Юнга сталі за методом деформації згину бруска.
Деякі теоретичні положення
Однією з основних деформацій твердого тіла є прогин стрижнів або брусків під дією сил, прикладених нормально до осі стрижнів. За деформацією згину можна визначити модуль Юнга. Для цього один кінець бруска закріплюють нерухомо, а до другого прикладають силу
Рис.1 Розглянемо теоретично деформацію згину бруска, яка здійснюється у результаті дії на нього моменту сили
Нехай цей елемент dx знаходиться на відстані х від вільного кінця бруска та безпосередньо прилягає до перерізу, який розглядається. І позначає напрямок цього перерізу перед згином, а ІІ – положення того ж самого перерізу після згину по відношенню до сусіднього перерізу, яке позначено – ІІІ. Перед згином І паралельний ІІІ. Знайдемо видовження dl деякого шару бруска висотою dy, який знаходиться на відстані у від нейтрального шару. З рис.2 видно, що
Для того щоб спричинити це видовження dl, на деякий шар бруска треба подіяти деякою елементарною пружною силою dF, яка за законом Гука буде дорівнювати
де Е – модуль Юнга матеріалу, з якого виготовлений брусок; ds – елементарна площа розтягнутого шару. Підставляючи у цей вираз вже знайдене значення
Щоб обчислити модуль обертального моменту пружної сили, яка діє на увесь поперечний переріз бруска, потрібно обчислити модулі моментів усіх елементарних пружних сил dF, які діють на нього, та просумувати їх. Модуль обертального моменту пружної сили визначимо за формулою:
Так як при рівновазі обертальний момент, який зумовлений дією пружних сил, повинен дорівнювати обертальному моменту зовнішньої сили
де Р – вага вантажу, який прикладений до вільного кінця бруска; х – відстань від точки прикладання сили Р до даного перерізу. Мірою прогину в перерізі, який розглядається, є елементарний кут dφ, який утворений двома напрямками І та ІІ поперечного перерізу. Легко бачити, що
Проведемо в точках А та В перпендикуляри до напрямків І та ІІ та продовжимо їх до вільного кінця бруска, зробивши, таким чином, їх довжину рівною х. Ясно, що ці два відрізки утворюють між собою кут, рівний dφ. Відстань dλ між кінцями обох відрізків є елементарна стріла прогину, який утворюється внаслідок обертання поперечного перерізу бруска, що розглядається. З рис.2 видно, що dλ = х dφ. Підставляючи сюди вже знайдене значення dφ, а також значення
з рівняння (5), знайдемо елементарну стрілу прогину
Вся стріла прогину може бути визначена у результаті інтегрування
З цієї формули можна визначити модуль Юнга матеріалу, з якого виготовлено брусок:
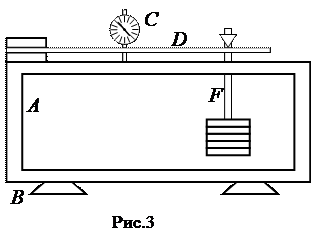
Опис установки
Схематичне зображення установки наведено на рис.3. Вона складається з масивної металевої рами A, яка встановлена на опорах B. На рамі встановлений індикатор циферблатного типу C, який можна пересувати по рамі. Цей прилад служить для вимірювання стріли прогину бруска D під дією вантажів, які поміщують на підвіс F. Брусок, виготовлений зі сталі, закріплений з одного боку нерухомо, а з іншого боку бруска на ньому встановлена опорна призма з підвіскою для вантажів F. Опорна призма може переміщуватись по бруску. Індикатор циферблатного типу (рис.4) широко використовують в експериментальних дослідженнях. Він, зокрема, служить для вимірювання малих деформацій тіл та їх видовження при нагріванні. Індикатор складається з корпуса 2, вимірювальної штанги 1, обойми зі шкалою 3, малої стрілки 5, великої стрілки 4. Система передачі зміни довжини предмета, який досліджується, здійснюється з допомогою штанги і важільного механізму, який знаходиться у корпусі приладу. Індикатор є точним вимірювальним приладом. Ціна однієї поділки його великої шкали складає 0,01 мм. Повний оборот великої стрілки відповідає зміні довжини досліджуваного предмета на 1 мм. Це фіксується відхиленням малої стрілки на одну поділку на малій шкалі. Значить, ціна однієї поділки малої шкали складає 1 мм. Максимальна зміна довжини, яку може зафіксувати індикатор, не перевищує 10 мм. Шкали індикатора мають чорну і червону розшифровку. За допомогою чорних цифр вимірюють величину видовження досліджуваного тіл, а за допомогою червоних цифр – укорочування розміру тіла. Перед початком вимірювань індикатор встановлюють на нуль поворотом обойми 3. Видовження чи укорочування тіла за допомогою індикатора визначають за формулою:
де
Рис.4 одного повного оберту, то зміна довжини тіла визначається за формулою
Вимірювання стріли прогину здійснюють за такою методикою. Поклавши на підвіс вантаж, визначають за індикатором стрілу прогину бруска у точці закріплення індикатора
Рис.5
Порядок виконання роботи. 1. Встановіть індикатор і опорну призму з підвісом на тих відстанях від місця прикріплення бруска до рами, значення яких вам задав керівник занять під час проведення допуску до виконання лабораторної роботи. Виміряйте ці відстані (відстань 2. За допомогою штангенциркуля виміряйте геометричні розміри стрижня a та b в місці його прикріплення до рами. Використовуючи наведені вище відомості, ознайомтесь з методикою вимірювання стріли прогину з допомогою індикатора циферблатного типу та закріпіть практичні навички роботи з цим приладом провівши пробні вимірювання. 3. Поступово навантажуючи брусок вантажами з відомою масою mi, відмітьте і запишіть показання індикатора циферблатного типу для кожного з використаних вантажів. Потім такі ж вимірювання повторіть в зворотному напрямку, поступово зменшуючи навантаження. Дослід проводять для трьох положень опорної призми з підвіскою. За формулою 4. З отриманих даних за формулою (13) розрахуйте стріли прогину бруска, які відповідають кожному з використаних вантажів. 5. За формулою (10) розрахуйте значення модуля Юнга Е сталі, з якої виготовлено брусок, для кожного з проведених дослідів. Розрахуйте середнє значення модуля Юнга Таблиця №1
Література: [1-13,19-38,47] Лабораторна робота №12
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (рис.1а), перпендикулярно до його осі. Внаслідок дії зовнішніх сил брусок деформується так, що його кінець опуститься, а поздовжня вісь викривиться. При згині верхні шари бруска будуть розтягуватись, його нижні шари – стискатись, а деякий середній шар, який називають нейтральним шаром, або пружною лінією бруска, не змінить свою довжину, він лише викривиться (рис.1б). Переміщення, яке здійснює вільний кінець бруска, називається стрілою прогину
(рис.1а), перпендикулярно до його осі. Внаслідок дії зовнішніх сил брусок деформується так, що його кінець опуститься, а поздовжня вісь викривиться. При згині верхні шари бруска будуть розтягуватись, його нижні шари – стискатись, а деякий середній шар, який називають нейтральним шаром, або пружною лінією бруска, не змінить свою довжину, він лише викривиться (рис.1б). Переміщення, яке здійснює вільний кінець бруска, називається стрілою прогину  . Стріла прогину буде тим більшою, чим більшим є навантаження. Вона також залежить від форми бруска, його розмірів і модуля Юнга матеріалу, з якого виготовлено брусок. Точний аналіз деформацій і напружень у пружному стрижні є досить складним. Наближені результати можна одержати, використовуючи гіпотезу Бернуллі про те, що при викривленні стрижня чи бруска усі його поперечні перерізи залишаються плоскими. Це завбачення відповідає наведеним вище даним про те, що у кожному малому об’ємі бруска при згині здійснюється тільки деформація стиску чи розтягу.
. Стріла прогину буде тим більшою, чим більшим є навантаження. Вона також залежить від форми бруска, його розмірів і модуля Юнга матеріалу, з якого виготовлено брусок. Точний аналіз деформацій і напружень у пружному стрижні є досить складним. Наближені результати можна одержати, використовуючи гіпотезу Бернуллі про те, що при викривленні стрижня чи бруска усі його поперечні перерізи залишаються плоскими. Це завбачення відповідає наведеним вище даним про те, що у кожному малому об’ємі бруска при згині здійснюється тільки деформація стиску чи розтягу.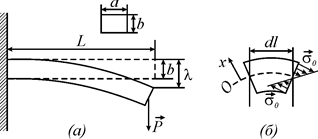
 Для того щоб обчислити стрілу прогину розглянемо деякий елемент dx прямокутного бруска довжиною L, висотою b та шириною a.
Для того щоб обчислити стрілу прогину розглянемо деякий елемент dx прямокутного бруска довжиною L, висотою b та шириною a. , звідки
, звідки 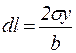 . (1)
. (1)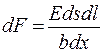 , (2)
, (2) , а також
, а також 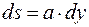 , що видно з рис.2, одержимо вираз за яким можна визначити елементарну пружну силу
, що видно з рис.2, одержимо вираз за яким можна визначити елементарну пружну силу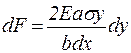 . (3)
. (3)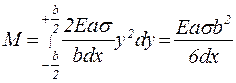 . (4)
. (4)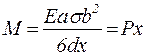 , (5)
, (5)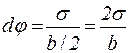 . (6)
. (6)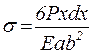 (7)
(7)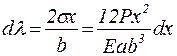 . (8)
. (8) . (9)
. (9)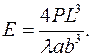 (10)
(10) та методики вимірювань.
та методики вимірювань. (11)
(11)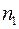 - число поділок малої шкали індикатора;
- число поділок малої шкали індикатора; 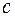 - ціна поділки великої шкали,
- ціна поділки великої шкали, 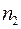 - число поділок великої шкали індикатора. Якщо велика стрілка при вимірювань не зробила ні
- число поділок великої шкали індикатора. Якщо велика стрілка при вимірювань не зробила ні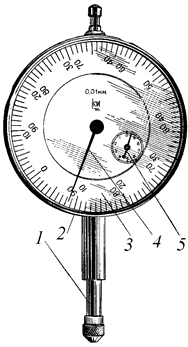
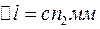 . (12)
. (12)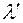 . З рис.5. видно, що дійсне значення стріли прогину
. З рис.5. видно, що дійсне значення стріли прогину 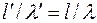 за формулою:
за формулою: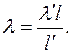 (13)
(13)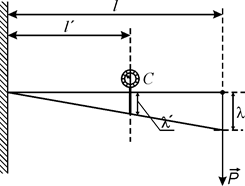
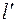 від місця прикріплення бруска до упора індикатора циферблатного типу та відстань
від місця прикріплення бруска до упора індикатора циферблатного типу та відстань 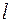 від місця закріплення бруска до опорної призми, на які висить платформа з вантажами) масштабною лінійкою.
від місця закріплення бруска до опорної призми, на які висить платформа з вантажами) масштабною лінійкою. розрахуйте вагу кожного з використаних вантажів
розрахуйте вагу кожного з використаних вантажів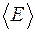 . Розрахуйте абсолютну і відносну похибки. Порівняйте одержане значення з відомими з довідників табличним значенням модуля Юнга сталі, яке наведене у довідковій таблиці Додатку №4. Дані, одержані під час вимірювань і у результаті розрахунків, запишіть у таблицю №1. Зробіть висновки.
. Розрахуйте абсолютну і відносну похибки. Порівняйте одержане значення з відомими з довідників табличним значенням модуля Юнга сталі, яке наведене у довідковій таблиці Додатку №4. Дані, одержані під час вимірювань і у результаті розрахунків, запишіть у таблицю №1. Зробіть висновки.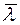 , м
, м
 ,
м
,
м
 ,
Па
,
Па



