
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Болонський процес та кредитно-модульна система організації навчального процесуСодержание книги
Поиск на нашем сайте ЗМІСТ
ПЕРЕДМОВА
У цьому навчальному посібнику зібрані нові описи експериментальних лабораторних робіт з механіки, які виконують студенти 1 курсу фізичного та радіофізичного факультетів Харківського національного університету імені В.Н. Каразіна при проходженні протягом одного семестру занять з фізичного практикуму на кафедрі експериментальної фізики. При підготовці цього видання його укладачами у тій чи іншій мірі були використані попередні варіанти описів лабораторних робіт, які викладені у посібниках [1-6], методичні, теоретичні і довідкові матеріали, що містяться у різноманітних підручниках та посібниках [7-47], а також власні методичні розробки. Фізичний практикум, під час якого студент особисто проводить експериментальні дослідження, опрацьовує теоретичний матеріал, оформляє звіт про лабораторну роботу, готується до її захисту, значно більше, ніж інші види занять з фізики, розвиває у нього теоретичні знання, прищеплює вміння і навички працювати самостійно. Це є особливо важливим у наш час у зв’язку з приєднанням України до Болонського процесу, згідно з яким значно посилюється роль самостійної роботи студентів у навчальному процесі, направленому на підвищення якості підготовки фахівців і підвищення рівня їх адаптації до зміни вимог ринку праці. У вступному занятті коротко описані загальні відомості щодо особливостей кредитно-модульної системи навчання, мети і завдання вивчення дисципліни «Фізика» у вищій школі та ролі лабораторних занять у навчальному процесі. У ньому також розглянуто методику обчислення похибок при опрацюванні результатів лабораторних робіт на практикумах із загального курсу фізики, подані рекомендації щодо графічного зображення та опрацювання результатів експерименту, наведено основні вимоги техніки безпеки, яких треба дотримуватись при проведенні занять в навчальній фізичній лабораторії. Описи кожної з 13 лабораторних робіт, які складають основний зміст посібника, укладено у повній відповідності із сучасними вимогами до навчально-методичних видань, що використовуються для забезпечення навчального процесу. Вони включають, як складові частини, підрозділи, за якими студенти можуть ознайомитись з деякими теоретичними відомостями щодо фізичних явищ, що досліджуються, а також з детальними методичними інструкціями щодо порядку підготовки до виконання лабораторної роботи, методик вимірювань, які використовуються в роботі, а також алгоритму їх проведення. У описах лабораторних робіт наведено також методичні рекомендації щодо обробки отриманих результатів та їх оформлення, а також подані посилання на підручники і посібники, з якими студенти можуть самостійно ознайомитись при підготовці до захисту лабораторних робіт. У додатках наведені питання для самоконтролю при підготовці до виконання та захисту експериментальних лабораторних робіт з механіки, приклади розрахунку похибок та різні довідкові таблиці. Подані у посібнику інструкції і рекомендації студенти повинні враховувати і використовувати при виконанні експериментальних лабораторних робіт, проявляючи разом з тим самостійність, наполегливість, ініціативу й творчість. Бажаємо студентам досягнути успіхів в дослідженнях різноманітних механічних явищ і в опануванні основними методами опрацювання результатів експериментів.
Укладачі посібника. I. ВСТУПНЕ ЗАНЯТТЯ
Похибки вимірювань фізичних величин
Класифікація вимірювань
Наукове спостереження полягає в цілеспрямованому і планомірному сприйнятті властивостей предметів і явищ дійсності для одержання відповідної інформації про об’єкт пізнання за допомогою органів чуття. У здійсненні наукового спостереження значну роль відіграє теоретичне мислення. Дослідник не просто реєструє факти. Він свідомо відшукує їх, користуючись певною ідеєю, гіпотезою тощо. Результати наукових спостережень відповідно інтерпретуються на основі певної теорії. У наукових спостереженнях широко використовують спеціальні засоби і прилади, які компенсують природну обмеженість органів чуттів людини, підвищують точність і об’єктивність результатів спостереження. Експеримент ґрунтується на забезпеченні відтворення явища в лабораторній обстановці і супроводжується точними, по можливості, вимірюваннями та математичною обробкою даних. За структурою експеримент суттєво відрізняється від спостереження наявністю спеціальних матеріальних засобів (експериментальних установок і приладів) впливу на досліджувані об’єкти або процеси. Вимірювання фізичних величин є метою кожної лабораторної роботи. Вимірювання – це порівняння способом фізичного експерименту даної фізичної величини з відомою однорідною величиною, взятою за одиницю вимірювання. У результаті встановлюється, у скільки разів вимірювана величина більша або менша від одиниці вимірювання. За способом знаходження результату вимірювання поділяють на два основні види: прямі і непрямі. Прямі вимірювання – це такі вимірювання, в яких шукане значення величини знаходять безпосередньо з досліду, порівнюючи його з мірою цієї величини за даними відліку, здійсненого за допомогою відлікового пристрою вимірювального приладу. Відліком у метрології прийнято називати число, відраховане по відліковому пристрою засобу вимірювання. Прикладом найпростіших прямих вимірювань може бути вимірювання довжини масштабною лінійкою, сили струму – амперметром, проміжків часу – секундоміром та ін. Непрямі вимірювання – це такі вимірювання, результат яких розраховують за відомою функціональною залежністю, вираженою аналітичною формулою, з використанням даних, одержаних в результаті проведення прямих вимірювань. Наприклад, об'єм прямокутного паралелепіпеда може бути знайдений за формулою
Похибки прямих вимірювань
При будь-якому вимірюванні фізичної величини, як би старанно його не проводили, неминучі похибки, тобто виміряти величину абсолютно точно неможна. Вимірювання фізичної величини не може бути проведене з абсолютною точністю з цілого ряду причин, таких як недоліки приладів, методів вимірювання, впливу зовнішніх умов, індивідуальних властивостей спостерігача та ін. Тому метою вимірювання є не тільки відшукання наближеного значення величини, а й оцінювання його відхилення від істинного значення. Обов'язково потрібно вказувати точність, гарантовану даним вимірюванням, або його похибку. Розрізняють абсолютні та відносні похибки. Похибку, виражену різницею між виміряним
Але істинне значення фізичної величини нам невідоме, тому можна знайти тільки наближену похибку, при цьому замість істинного значення величини беруть найбільш ймовірне її значення, яке за великої кількості вимірювань дорівнює середньому арифметичному всіх виміряних значень. Виміряне значення Якість результатів вимірювання краще характеризує відносна похибка. Відносну похибку визначають відношенням абсолютної похибки до дійсного (середнього арифметичного) значення величини. Цю похибку виражають у процентах (відсотках):
Відносна похибка дозволяє зробити висновки про точність проведених вимірювань. У технічній літературі часто зустрічається поняття «точність вимірювань». Під цим розуміють величину, обернену до відносної похибки вимірювань без процентів. Так, якщо Вимірювання залежно від методу, приладів та властивостей об’єкта дослідження можуть бути з одноразовими або багаторазовими спостереженнями. Відповідно перші називають звичайними вимірюваннями, а другі – статистичними вимірюваннями. Похибки вимірювань за характером і причинами їх появи поділяють на три класи: систематичні, випадкові та промахи. Систематична похибка – це та частина загальної похибки вимірювання, яка залишається сталою або змінюється закономірно при повторних вимірюваннях тієї самої величини. Систематична похибка має знак і викликає відхилення результату завжди в один бік. Через це дослідник, частіше за все, просто не підозрює про існування такої похибки. Причини виникнення систематичної похибки такі: неправильне градуювання приладу або його несправність; неправильне встановлення приладу та погані умови його роботи; невдалий вибір методу дослідження і т. д. Виявлення, оцінювання та позбавлення від систематичних похибок є головними завданнями дослідника. Для цього необхідно ретельно готуватись до проведення вимірювання і продумувати методику його проведення. Наведемо деякі приклади. Якщо шкала приладу зміщена, то всі вимірювання матимуть сталу похибку, що дорівнює величині зміщення. Або коли металевою лінійкою вимірювати розміри тіла безпосередньо в нагрівальній печі. Внаслідок термічного розширення лінійки при її нагрівання збільшиться відстань між поділками лінійки і систематична похибка дорівнюватиме величині цього збільшення. В обох прикладах систематична похибка може бути виявлена. Несправний прилад можна порівняти з іншим аналогічним приладом, а температурну похибку можна розрахувати за температурним коефіцієнтом матеріалу лінійки. Але це зовсім не означає, що завжди можна повністю позбавитися систематичної похибки. Завжди існує власна похибка навіть у справного приладу, зумовлена недоліками його виготовлення. Таку похибку називають інструментальною похибкою. Поділки на шкалі приладу роблять відповідно до його інструментальної похибки. Масштабну лінійку градуюють через Аналогічну ситуацію маємо при зважуванні тіла за допомогою гир. У паспорті вказується, що гиря масою
За відсутності вказівок щодо похибки вимірювального приладу його абсолютну похибку беруть такою, що дорівнює половині ціни найменшої поділки його шкали. Випадкова похибка. З досвіду відомо, що багаторазові вимірювання тієї самої величини, проведені найточнішими приладами, дають значення, які дещо відрізняються одне від одного. У такому випадку має місце випадкова похибка, складова загальної похибки, що змінюється довільним чином при повторних вимірюваннях однієї величини. Поява випадкових похибок зумовлена конструкцією приладу (тертя між деталями та ін.), зміною зовнішніх умов (коливання температури, вібрації та ін.), а також суб’єктивним впливом на процес вимірювання самого спостерігача. Неможливо позбавитися випадкових похибок, але ми можемо зменшити їх вплив на кінцевий результат, використовуючи методи математичної статистики, що дозволяють визначити, яке зі значень найближче до істинного, та знайти похибку цього значення. Теорія похибок установлює що: 1.При багатократному вимірюванні однієї і тієї самої величини однакова ймовірність одержання значень як більших за істинне, так і менших, тому найближчим до істинного значення буде середнє арифметичне значення
де Значення 2.Результати окремих вимірювань відрізняються від
Ця різниця наближена до абсолютної похибки окремого вимірювання і є випадковою величиною. Середнє значення відхилення від середнього арифметичного, яке за своєю величиною близьке за величиною до середнього значення абсолютної похибки кількох вимірювань, знаходять за формулою:
Промахи. Про те, що під час проведення вимірювань були допущені грубі похибки (промахи), дізнаються здебільшого наприкінці досліджень, коли дістануть явно неправильні результати. Таким чином, можемо визначити промах як похибку, що суттєво перевищує очікувану за даних умов. Джерелом такої похибки може бути неуважність або помилка експериментатора, а також несправність засобу вимірювання. Якщо у результаті аналізу даних, одержаних під час проведення вимірювань, дослідник дійшов висновку, що результати вимірювань містять промахи, то ці, завідомо неправильні дані слід беззастережно відкинути. Після чого бажано встановити причину помилки, виправити несправності та недоліки і повторити вимірювання заново.
Наближені обчислення
Важливим питанням є те, скільки значущих цифр слід зберігати в результаті кожної дії. Точність обчислень результатів вимірювання має відповідати точності вимірювань. Виконувати обчислення з точністю, більшою ніж це дозволяють експериментальні дані, нераціонально і некоректно. Отже, обчислення, які виконуються при математичній обробці експериментальних результатів, отриманих у науковій чи навчальній лабораторії, є наближеними. Одержані числа можна округляти, тобто зменшувати кількість їх значущих цифр. Щоб округлити число до n значущих цифр, треба відкинути усі цифри, які стоять після n-го розряду. При цьому користуються такими правилами: якщо перша з цифр, які відкидають менша 5, то остання з тих цифр, які залишаються, не змінюється; якщо ж перша з цифр, які відкидають, більша або рівна 5, то остання цифра, з тих цифр, які зберігаються, збільшується на одиницю. Наприклад, округлення числа 7,192 до трьох значущих цифр дає число 7,19, до двох 7,2. Округлення числа 1681 до двох значущих цифр дає число У наближених обчисленнях записи 25,6 і 25,600 відрізняються один від одного. У числі 25,6 точні (правильні) лише цифри цілих і їхні десяті частини, а в числі 25,600 також соті і тисячні частини. Прийнято вважати, що k -та цифра наближеного числа а точною (правильною), якщо абсолютна похибка цього числа не перевищує половини одиниці k-го розряду цієї цифри. Всі цифри, які стоять лівіше від правильної, також правильні. У протилежному випадку цифру k-го розряду називають сумнівною. Сумнівною цифрою називають ту, яка стоїть безпосередньо за крайньою справа правильною цифрою. Цифри, які стоять справа від сумнівної цифри, називаються неправильними. Неправильні цифри повинні бути відкинуті шляхом округлення як у вихідних даних, так і у кінцевому результаті розрахунку. Всі правильні цифри числа, починаючи з першої зліва, відмінної від нуля, і включаючи першу сумнівну цифру, називаються значущими цифрами. Всі інші цифри називаються незначущими. Наприклад, у числі 0,0507 три значущих цифри; перші два нулі незначущі, нуль між п’ятіркою і семіркою – значущий. Записуючи остаточні результати наближених обчислень, незначущі цифри числа відкидають. У числі 2500 – чотири значущих цифри (нулі в числі 2500 – значущі цифри; точно відомо, що одиниць і десятків у числі 2500 немає). Запис 47200·103 або 0,47200·108 означає, що в числі 47 200 000 три останні цифри не значущі, а всі інші – значущі. Запис результатів вимірювання має відповідати також точності вимірювання. Наприклад, якщо товщина пластинки після обчислень становить 4,5568 мм при абсолютній похибці вимірювання 0,02 мм, то такий запис числа не відповідає теорії похибок вимірювання. Середнє арифметичне значення для товщини пластинки в цьому разі слід округлити до 4,56 мм. Взагалі при округленні наближеного або точного числа а до n значущих цифр за правилом доповнення число а замінюють числом Якщо з наближеними числами ще проводитимуться обчислення, то в них слід зберігати одну або дві сумнівні цифри. При виконанні математичних операцій над наближеними числами слід дотримуватись таких правил. Наближені числа треба округляти перед виконанням відповідних математичних операцій. Округляти числа слід за наведеним вище правилом до розряду найменш точного числа, залишаючи в числах одну або дві запасні цифри. Це дає змогу цілком правильно округлити кінцевий результат. У кінцевому результаті ці «запасні» цифри відкидають. При додаванні і відніманні наближених чисел кінцевий результат слід округляти так, щоб у ньому не було значущих цифр у тих розрядах, яких немає хоча б в одному з наближених чисел. Наприклад: 5,962 + 2,49 + 7,18376 + 6,1468 При множенні і діленні наближених чисел у кінцевому результаті слід залишати стільки значущих цифр, скільки їх є в наближеному числі з найменшою кількістю значущих цифр. Наприклад: 3,624·2,4·5,1127·3,62·2,4·5,11=8,688 При піднесенні до степеня в кінцевому результаті слід залишити стільки значущих цифр, скільки їх має наближене число, яке підноситься до степеня. Наприклад: (1,26)2=3,276 При добуванні коренів у кінцевому результаті слід залишити стільки значущих цифр, скільки їх має підкореневе наближене число. Наприклад: Знаходячи логарифм наближеного числа, потрібно брати з таблиць чи з дисплея мікрокалькулятора для мантиси стільки значущих цифр, скільки їх має це число. Наприклад: lg77,23 Правильне і обернене: число, яке знаходять за логарифмом, повинно мати стільки значущих цифр, скільки їх у мантиси (при довільній характеристиці). На основі викладеного вище, сформулюємо правила запису вимірювань і розрахунків, яких слід дотримуватись у навчальній лабораторії: 1. Остаточні результати вимірювань і розрахунків записують разом з їх абсолютною похибкою. 2. При запису похибок обмежуються однією (інколи двома значущими цифрами). Остання цифра результатів і остання цифра його абсолютної похибки повинні належати до одного і того ж самого десятинного розряду. Приклад правильного запису: 3..Якщо в похибці перша значуща цифра одиниця, то після неї зберігається ще одна, а в результаті дві сумнівні цифри. Приклад правильного запису: 4. Якщо у відповіді міститься множник виду 10n, то і у результаті, і у його абсолютній похибці він повинен бути однаковим. Приклад правильного запису: 5. Вимірювана величина і її абсолютна похибка виражаються в одних одиницях вимірювань. Приклад правильного запису: 6. Абсолютна похибку також треба округляти до однієї (іноді до двох) значущих цифр. Детальніше ознайомитись з методами обробки експериментальних результатів і розрахунку похибок можна за посібниками [7-9,11,19,39,40,43-46].
Завдання №4. 1. Зважте одне і теж саме тіло за методом Борда та за методом Гаусса. Порівняйте отримані результати. Зробіть висновок щодо переваг і недоліків зазначених методів точного зважування. 2. Розрахуйте абсолютну похибку визначення маси зважуваних тіл. Література: [1-15,17,16] Лабораторна робота №2
Вивчення прецесії гіроскопа
Мета лабораторної роботи: Ознайомлення з особливостями руху гіроскопа. Визначення кутової швидкості прецесії і моменту інерції гіроскопа.
Деякі теоретичні положення Гіроскопом називається масивне симетричне тверде тіло, яке здатне обертатись навколо власної осі симетрії з великою кутовою швидкістю (рис.1).
Рис.1 Встановлено, що якщо вісь гіроскопа, який обертається з великою кутовою швидкістю, розташована вертикально, то його обертання може тривати дуже довго. Якщо вісь відхилиться від вертикалі, то гіроскоп, не впаде, а буде здійснювати так званий прецесійний рух, його вісь буде описувати поверхню кругового конуса з вершиною у точці опори
Рис.2
Прецесія – це складний рух, яке складається з обертання гіроскопа навколо двох осей, які перетинаються. Навколо власної осі він обертається з кутовою швидкістю Кутова швидкість Якщо на вісь гіроскопа діє деяка сила, яка створює момент сили
Аналіз рівняння (1) спрощується внаслідок того, що кутова швидкість обертання гіроскопа дуже велика. Це означає, що головний момент імпульсу практично направлений по осі гіроскопа. Момент зовнішніх сил
Якщо при зміні напряму осі на кут
Враховуючи, що для гіроскопа, який швидко обертається,
де
Отже, обертання осі гіроскопа з кутовою швидкістю
Опис приладу та методики вимірювань
Прилад (рис.3) складається з електричного моторчика А, закріпленого в обоймі В. Обойма опирається на вертикальний стрижень С і може обертатись навколо горизонтальної осі, а разом зі стрижнем – навколо вертикальної. Власне гіроскопом є ротор моторчика з масивним диском Е. Момент зовнішніх сил, прикладених до гіроскопа, може змінюватись при переміщенні вантажу К по стрижню обойми. Прилад має також електронний блок G, у склад якого входять: система вимірювання швидкості обертання моторчика, електронний таймер, фотоелектрична система вимірювання кута повороту гіроскопа навколо вертикальної осі.
Рис.3 Увімкнення моторчика здійснюється шляхом виведення ручки «скорость вращения» 1 із крайнього лівого положення. Подальше обертання цієї ручки за годинниковою стрілкою приводить до збільшення швидкості обертання моторчика. Стрілковий прилад 2 на панелі блоку показує швидкість обертання моторчика. Увімкнення електронного таймера і фотоелектричної системи вимірювання кута
Порядок виконання роботи 1. Закріпіть вантаж К на стрижні обойми так, щоб увесь прилад знаходився у байдужій рівновазі. Вісь гіроскопа встановіть горизонтально. 2. Увімкніть моторчик і зачекавши 2-3 хвилини, доки ротор не почне обертатись з номінальним числом оборотів. 3. Зміщенням вантажу К створіть момент сили тяжіння М. Величина цього моменту визначається за формулою 4. Виміряйте величину кутової швидкості прецесії при різних значеннях моменту
5. Скориставшись формулою (6) визначте середнє арифметичне значення величини 6. За формулою (4) обчисліть момент інерції гіроскопа Література: [11,16,20-38] Додаток №1 Питання для самоконтролю при підготовці до виконання та захисту експериментальних лабораторних робіт з механіки.
Деякі математичні формули. Приклади розрахунку Приклад №1. I. Робоча формула, яка використовується для розрахунку прискорення сили тяжіння земного за періодом коливань математичного маятника, має такий вигляд:
ІІ. Результати прямих експериментальних вимірювань та табличні значення величин, виражені у одиницях СГС є такими. Нехай
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.017 с.) |

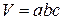 , де
, де  – ребра паралелепіпеда, довжина яких виміряна шляхом проведення прямих вимірювань за допомогою штангенциркуля або лінійки.
– ребра паралелепіпеда, довжина яких виміряна шляхом проведення прямих вимірювань за допомогою штангенциркуля або лінійки. і істинним
і істинним 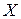 значеннями величини, називають абсолютною похибкою вимірювання. Вона визначається за формулою
значеннями величини, називають абсолютною похибкою вимірювання. Вона визначається за формулою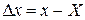 . (1)
. (1)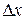 може бути як додатною, так і від'ємною, Але абсолютна похибка не дає повного уявлення про точність вимірювання, оскільки її величина не порівнюється із самою виміряною величиною.
може бути як додатною, так і від'ємною, Але абсолютна похибка не дає повного уявлення про точність вимірювання, оскільки її величина не порівнюється із самою виміряною величиною.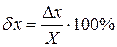 . (2)
. (2) , то точність таких вимірювань дорівнюватиме 100.
, то точність таких вимірювань дорівнюватиме 100. , а мікрометр має поділки, найменша ціна яких дорівнює одній сотій міліметра. На перший погляд здається, що за допомогою лупи можна провести підрахунок десятих, а то й сотих часток міліметра і на лінійці. Але це не так. Товщина самих поділок уже дає десяту частку міліметра, і нанесені вони з деякою похибкою, тому при вимірюванні лінійкою можна гарантувати мінімальну похибку, яка дорівнює ціні поділки, або
, а мікрометр має поділки, найменша ціна яких дорівнює одній сотій міліметра. На перший погляд здається, що за допомогою лупи можна провести підрахунок десятих, а то й сотих часток міліметра і на лінійці. Але це не так. Товщина самих поділок уже дає десяту частку міліметра, і нанесені вони з деякою похибкою, тому при вимірюванні лінійкою можна гарантувати мінімальну похибку, яка дорівнює ціні поділки, або  має інструментальну абсолютну похибку
має інструментальну абсолютну похибку  Таку похибку дають усій партії гир, порівнюючи вибірково деякі з них з еталоном. При цьому в жодному випадку похибка не перевищує
Таку похибку дають усій партії гир, порівнюючи вибірково деякі з них з еталоном. При цьому в жодному випадку похибка не перевищує 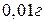 , але може бути меншою. Та нам це невідомо, тому маси тіл, виміряні за допомогою такої гирі,
, але може бути меншою. Та нам це невідомо, тому маси тіл, виміряні за допомогою такої гирі,  повинні мати похибку
повинні мати похибку  У цьому випадку інструментальна похибка є систематичною і тому при повторних вимірюваннях завжди дає відхилення виміряної величини від істинного значення в один бік, але невідомо в який. Отже, похибка подається з подвійним знаком і результат зважування запишеться так:
У цьому випадку інструментальна похибка є систематичною і тому при повторних вимірюваннях завжди дає відхилення виміряної величини від істинного значення в один бік, але невідомо в який. Отже, похибка подається з подвійним знаком і результат зважування запишеться так: .
. ряду окремих вимірювань
ряду окремих вимірювань 
 , (3)
, (3)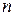 кількість вимірювань.
кількість вимірювань.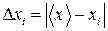 . (4)
. (4)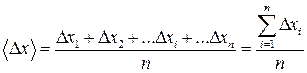 . (5)
. (5)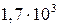 , а округлення числа 0,80214 – число 0,8. Абсолютна похибка округленого числа не перевищує половини одиниці останньої збереженої цифри. Це, зокрема, слід враховувати при округленні табличних даних та значень фізичних сталих, які беруть з довідкових таблиць.
, а округлення числа 0,80214 – число 0,8. Абсолютна похибка округленого числа не перевищує половини одиниці останньої збереженої цифри. Це, зокрема, слід враховувати при округленні табличних даних та значень фізичних сталих, які беруть з довідкових таблиць.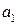 з n значущими цифрами так, щоб похибка округлення не перевищувала половини одиниці розряду, що зберігається.
з n значущими цифрами так, щоб похибка округлення не перевищувала половини одиниці розряду, що зберігається.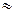 5,962+2,49+7,184 + +6,147=21,783
5,962+2,49+7,184 + +6,147=21,783  .
.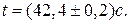 Приклад неправильного запису:
Приклад неправильного запису: 
 . Приклад неправильного запису:
. Приклад неправильного запису:  .
.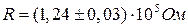 . Приклад неправильного запису:
. Приклад неправильного запису:  .
. . Приклад неправильного запису
. Приклад неправильного запису  .
.
 (рис.2).
(рис.2).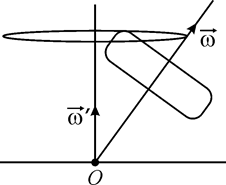
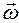 , а навколо нерухомої вертикальної осі з кутовою швидкістю
, а навколо нерухомої вертикальної осі з кутовою швидкістю 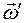 . Точка перетину двох осей є єдиною нерухомою точкою гіроскопа. У прикладі, який розглядається на рис.2, – це точка опори
. Точка перетину двох осей є єдиною нерухомою точкою гіроскопа. У прикладі, який розглядається на рис.2, – це точка опори  , то момент імпульсу відносно точки
, то момент імпульсу відносно точки 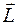 змінюється у відповідності з рівнянням моментів
змінюється у відповідності з рівнянням моментів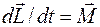 . (1)
. (1)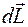 повинно бути направлене перпендикулярно до вектора
повинно бути направлене перпендикулярно до вектора  , то відповідна зміна модуля вектора моменту імпульсу буде дорівнювати
, то відповідна зміна модуля вектора моменту імпульсу буде дорівнювати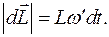 (2)
(2)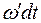 момент зовнішньої сили повернеться на такий же кут і не змінить свою величину, то ситуація у новому положенні гіроскопа буде аналогічною, тобто відбудеться так ж сама зміна напряму осі обертання гіроскопа за наступний момент часу
момент зовнішньої сили повернеться на такий же кут і не змінить свою величину, то ситуація у новому положенні гіроскопа буде аналогічною, тобто відбудеться так ж сама зміна напряму осі обертання гіроскопа за наступний момент часу 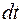 , тобто під дією постійного моменту сил
, тобто під дією постійного моменту сил 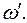 При цьому зміна моменту імпульсу за одиницю часу, рівне
При цьому зміна моменту імпульсу за одиницю часу, рівне 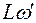 , буде визначатися рівнянням (1) і дорівнювати
, буде визначатися рівнянням (1) і дорівнювати . (3)
. (3)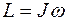 , (4)
, (4)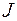 - момент інерції гіроскопа відносно його осі, одержимо формулу для визначення модуля вектора кутової швидкості прецесії
- момент інерції гіроскопа відносно його осі, одержимо формулу для визначення модуля вектора кутової швидкості прецесії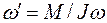 . (5)
. (5)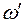 відносно його осі під дією постійного моменту сил, називається прецесією гіроскопа.
відносно його осі під дією постійного моменту сил, називається прецесією гіроскопа.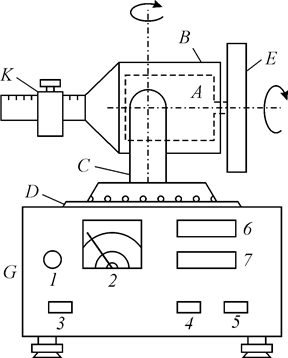
 повороту гіроскопа навколо горизонтальної осі здійснюється шляхом натискання клавіші «сеть» 3. При натисканні на клавішу «сброс» 4 здійснюється обнулювання табло електронного блока 6, 7. Після натискання на клавішу «сброс» здійснюється запуск фотоелектронної системи вимірювання кута
повороту гіроскопа навколо горизонтальної осі здійснюється шляхом натискання клавіші «сеть» 3. При натисканні на клавішу «сброс» 4 здійснюється обнулювання табло електронного блока 6, 7. Після натискання на клавішу «сброс» здійснюється запуск фотоелектронної системи вимірювання кута 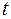 .
.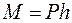 , де
, де 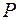 - заданий модуль ваги вантажу,
- заданий модуль ваги вантажу, 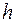 - відстань цього вантажу від його початкового положення, яка вимірюється за шкалою на стрижні.
- відстань цього вантажу від його початкового положення, яка вимірюється за шкалою на стрижні.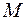 (при різних значеннях плеча
(при різних значеннях плеча 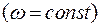 в межах похибки вимірювань повинна виконуватись така умова
в межах похибки вимірювань повинна виконуватись така умова 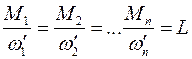 . (6)
. (6) 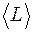 для кожного значення кутової швидкості обертання ротора
для кожного значення кутової швидкості обертання ротора 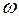 .
. 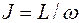 для кожного значення кутової швидкості обертання ротора
для кожного значення кутової швидкості обертання ротора 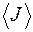 . Обчисліть абсолютну та відносну похибки.
. Обчисліть абсолютну та відносну похибки. 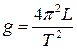 . (1)
. (1) - довжина маятника, яка виміряна з абсолютною похибкою
- довжина маятника, яка виміряна з абсолютною похибкою  . Період коливань маятника <
. Період коливань маятника < 


