
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вивчення обертального руху твердого тіла за допомогою маятника Обербека.Содержание книги
Поиск на нашем сайте
Мета лабораторної роботи: Вивчення основного закону динаміки обертального руху твердого тіла, визначення моменту інерції хрестовини маятника Обербека.
Деякі теоретичні відомості. Твердим тілом (або абсолютно твердим тілом) у механіці називають систему матеріальних точок (елементів тіла), відстань між якими у процесі руху не змінюються. Згідно з визначенням тверде тіло не деформується під дією зовнішніх сил. Реальне тверде тіло можна вважати твердим тілом, якщо деформації, що виникають під дією зовнішніх сил, малі і в умовах задачі ними можна знехтувати. Обертальним рухом твердого тіла навколо нерухомої осі називається рух, при якому існують хоч би дві нерухомі точки тіла. Пряма лінія, яка проходить через ці точки, називається віссю обертання. Можна показати, що усі інші точки тіла, які не лежать на осі обертання, рухаються в перпендикулярній до осі обертання площині по колах, центри яких лежать на осі обертання. Лінійна швидкість цих точок перпендикулярна до осі обертання і направлена по дотичній до кола. Основними кінематичними характеристиками обертального руху твердого тіла є його кутова швидкість і кутове прискорення.
правилом: воно утворює правий гвинт з додатнім напрямком осі z декартової системи координат. Кут Нехай тверде тіло повернулося на нескінченно малий кут
Кутовим прискоренням називається вектор
Напрямок вектора
Зв’язок між векторами кутової швидкості
де Основними динамічними характеристиками обертального руху є момент сили, момент імпульсу і момент інерції. Між поступальним і обертальним рухом існує аналогія. Момент сили
Рис.5 Момент сили відносно нерухомої точки О, яка лежить на вісі обертання, – це фізична величина, яка визначається векторним добутком радіуса вектора
Вектор момента сили напрямлений вздовж вісі обертання відповідно до правила правого буравчика: якщо обертати буравчик від радіуса-вектора
добутком радіуса-вектора
Напрямок вектора моменту імпульсу матеріальної точки визначається за правилом правого буравчика. Якщо обертати буравчик від радіуса-вектора Між моментом сили
Дослід показує, що зміна швидкості обертального руху твердого тіла, тобто його кутове прискорення, залежить не тільки від маси твердого тіла, що обертається, але й від її розподілу відносно нерухомої вісі обертання. Величина, яка враховує обидві ці обставини, і виступає мірою інертності твердого тіла у обертальному русі, називається моментом інерції твердого тіла відносно нерухомої вісі обертання J. Встановимо зв’язок між моментом імпульсу і моментом інерції твердого тіла. Як відомо, кутове переміщення точок твердого тіла в процесі його обертального руху виникає внаслідок дії на тверде тіло деякого моменту сил. При цьому на кожний елемент
Рис.7
Момент цієї сили відносно довільної точки А, яка лежить на нерухомій вісі ОО',
Сумарний момент сил, який діє на все тверде тіло, що складається з N елементів маси, визначається за формулою:
Скалярна величина
Користуючись формулами (11) та (12), отримаємо формулу, яка також виражає закон динаміки обертального руху твердого тіла:
З рівняння (13) бачимо, що вектор моменту сили
Залежність модуля кутового прискорення від модуля обертального моменту сили та моменту інерції відносно нерухомої вісі обертання можна визначити експериментально за допомогою хрестоподібного маятника Обербека (рис.7).
Рис.8
Опис експериментальної установки.
Основна частина цього маятника – хрестовина – складається зі шківа та чотирьох легких стрижнів, які закріплені (вгвинчені) у шків, перпендикулярно осі шківа. Хрестовина може обертатися відносно нерухомої горизонтальної вісі ОО', яка співпадає з віссю шківа. На кожному зі стрижнів хрестовини закріплюють по одному додаткові вантажі, які мають циліндричну форму. Маси вантажів m0 однакові. Їх величина вказана на установці. З метою зміни моменту інерції приладу вантажі m0 можна переміщувати вздовж стрижнів та закріплювати на будь-яких відстанях Ri від осі обертання маятника ОО'. На шків намотана в один шар тонка, але доволі міцна нитка. До вільного кінця нитки прив’язана платформа П відомої маси. На платформу кладуть вантаж масою m. Якщо нитці дати можливість розмотуватися у результаті падіння платформи з вантажем масою m, то вона буде натягуватись. Сила натягу нитки створює обертальний момент сили. Під дією цього моменту сили маятник Обербека почне обертатися з кутовим прискоренням.
Звідси
Момент сили натягу нитки відносно вісі обертання ОО¢
де r – радіус шківа (плече сили натягу нитки). У свою чергу, як вже зазначено вище,
де JОО¢ - момент інерції маятника відносно вісі обертання ОО¢, b - кутове прискорення маятника. Кутове прискорення маятника можна визначити з таких міркувань. Нехай платформа з вантажем масою m падає з висоти h. Тоді прискорення його руху визначається за формулою
Якщо умови експерименту такі, що у його ході нитка змотується із шківа маятника без тертя і ковзання, то лінійне (тангенціальне) прискорення точок його поверхні також дорівнює а. Тоді величину кутового прискорення можна визначити за формулою
Момент інерції J маятника відносно осі ОО', який, як відомо, є скалярною адитивною величиною, є сумою моменту інерції хрестовини без додаткових вантажів – Jхр та моменту інерції додаткових вантажів m0 –
Момент інерції додаткового вантажу можна визначити аналітично, якщо прийняти його за матеріальну точку, яка знаходиться на відстані Ri від вісі обертання. Як відомо, у цьому випадку момент інерції одного додаткового вантажу
Остаточно, враховуючи вираз (22), момент інерції хрестовини можна визначити за такою формулою
Порядок виконання роботи.
1. Виміряйте лінійкою висоту падіння тягарців h, а штангенциркулем – радіус шківа r. Усередніть результати, отримані у ході проведення не менше ніж трьох вимірювань. Дані запишіть у таблицю №1. 2. Закріпіть додаткові вантажі на кінцях стрижнів симетрично до вісі обертання і на однакових відстанях від вісі обертання та виміряйте лінійкою відстань Ri від вісі обертання до центра мас вантажу m0. Усередніть результати, отримані у ході проведення не менше ніж трьох вимірювань. Дані запишіть у таблицю №1. 3. Послідовно навантажуючи платформу П, що підвішена до кінця нитки, яка намотана на шків в один шар, тягарцями, маси яких mі відомі, визначте, користуючись секундоміром, час падіння t кожного з тягарців маси mі з висоти h. Усередніть результати, отримані у ході не менше ніж трьох вимірювань. Дані запишіть у таблицю№1. 4. За формулами (19) і (20) розрахуйте модулі лінійного а та кутового прискорення b, а за формулою (17) момент сили натягу нитки М відносно нерухомої вісі обертання. Дані розрахунків запишіть у таблицю №1. 5. Змістіть центри мас усіх чотирьох додаткових вантажів m0 на два сантиметри ближче до вісі обертання і закріпіть їх на однаковій відстані від вісі обертання Ri. Виміряйте лінійкою цю відстань. Дані запишіть у таблицю №1. За методикою, описаною у п.3 і п.4, проведіть вимірювання і розрахунки для даного значення Ri. 6. Змістіть центри мас усіх чотирьох додаткових вантажів m0 ще на два сантиметри ближче до осі обертання і закріпіть їх на однаковій відстані від осі обертання Ri. Виміряйте лінійкою цю відстань. Дані запишіть у таблицю №1. За методикою, описаною у п.3 і п.4, проведіть вимірювання і розрахунки для даного значення Ri. 7. За значенням Мі та βі для кожного значення Rі побудуйте графіки залежностей М=f(b). З кожного з графіків визначте момент інерції маятника Обербека Ji відносно нерухомої осі обертання OO, скориставшисьтакою формулою
8. За формулою (22) обчисліть момент інерції додаткових вантажів для кожного із значень Ri, а за формулою (23) визначте значення моменту інерції хрестовини маятника Обербека Jхр. Дані, отримані у результаті розрахунків, запишіть у таблицю №1. Розрахуйте середнє значення моменту інерції хрестовини маятника Обербека відносно нерухомої вісі Таблиця №1
Література: [1-16,20-35] Лабораторна робота №5
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.43 (0.008 с.) |

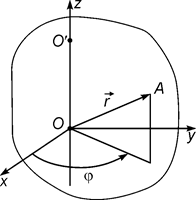 Рис.1
Рис.1
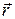 . Кутовою координатою (кутом повороту) називається кут
. Кутовою координатою (кутом повороту) називається кут 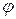 між додатним напрямком вісі x і проекцією радіуса вектора
між додатним напрямком вісі x і проекцією радіуса вектора 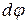 навколо нерухомої вісі ОО¢. При цьому довільна точка А тіла, рухаючись по колу, зайняла положення А (рис.2). Вектором елементарного повороту називається вектор
навколо нерухомої вісі ОО¢. При цьому довільна точка А тіла, рухаючись по колу, зайняла положення А (рис.2). Вектором елементарного повороту називається вектор 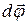 , модуль якого дорівнює модулю кута повороту
, модуль якого дорівнює модулю кута повороту 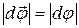 . Вектор
. Вектор 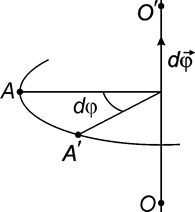 Рис.2
Рис.2
 . Кутовою швидкістю тіла називається вектор, який визначається за такою формулою:
. Кутовою швидкістю тіла називається вектор, який визначається за такою формулою:
 , (1)
, (1)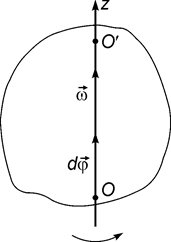 Рис.3
Рис.3
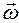 співпадає за напрямком з вектором
співпадає за напрямком з вектором 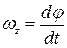 . (2)
. (2) , який дорівнює першій похідній вектора кутової швидкості за часом, або другій похідній вектора кутового переміщення за часом:
, який дорівнює першій похідній вектора кутової швидкості за часом, або другій похідній вектора кутового переміщення за часом: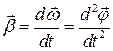 . (3)
. (3)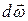 прирощення кутової швидкості за нескінченно малий проміжок часу dt. Якщо тіло обертається навколо нерухомої вісі обертання ОО', то вектор прирощення кутової швидкості
прирощення кутової швидкості за нескінченно малий проміжок часу dt. Якщо тіло обертається навколо нерухомої вісі обертання ОО', то вектор прирощення кутової швидкості 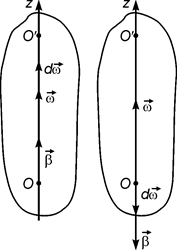 Рис.4
Рис.4
 направлені в одну сторону, а якщо кутова швидкість у ході обертання тіла зменшується, то вектор кутового прискорення
направлені в одну сторону, а якщо кутова швидкість у ході обертання тіла зменшується, то вектор кутового прискорення 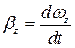 . (4)
. (4) від вісі обертання, такий:
від вісі обертання, такий: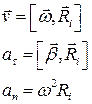 , (5)
, (5)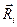 - радіус-вектор даної точки,
- радіус-вектор даної точки,  - тангенціальне прискорення цієї точки,
- тангенціальне прискорення цієї точки, 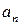 - нормальне прискорення цієї точки.
- нормальне прискорення цієї точки. є аналогом сили, момент імпульсу
є аналогом сили, момент імпульсу 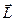 - аналогом імпульсу, а момент інерції J – аналогом маси.
- аналогом імпульсу, а момент інерції J – аналогом маси.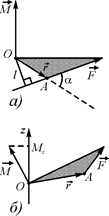
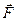
 . (6)
. (6) (рис.5). Модуль вектора моменту сили дорівнює добутку модуля вектора сили на найкоротшу відстань від точки О до лінії дії сили, або добутку модуля вектора сили на плече сили.
(рис.5). Модуль вектора моменту сили дорівнює добутку модуля вектора сили на найкоротшу відстань від точки О до лінії дії сили, або добутку модуля вектора сили на плече сили.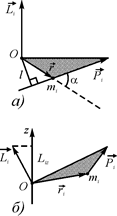 Рис.6
Рис.6
 матеріальної точки
матеріальної точки 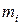 відносно нерухомої точки О, яка лежить на осі обертання, – це фізична величина, яка визначається векторним
відносно нерухомої точки О, яка лежить на осі обертання, – це фізична величина, яка визначається векторним
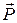
 . (7)
. (7)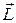 існує зв’язок, який встановлюється основним рівнянням динаміки обертального руху твердого тіла:
існує зв’язок, який встановлюється основним рівнянням динаміки обертального руху твердого тіла: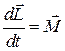 . (8)
. (8)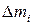 маси твердого тіла (рис.7), яке рухається з лінійною швидкістю
маси твердого тіла (рис.7), яке рухається з лінійною швидкістю  , діє тангенціальна сила
, діє тангенціальна сила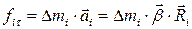 . (9)
. (9)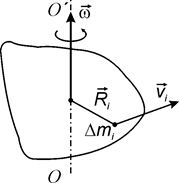
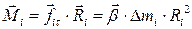 . (10)
. (10) . (11)
. (11)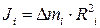 називається моментом інерції і -того елемента маси твердого тіла відносно нерухомої вісі ОО'. Момент інерції усього твердого тіла визначається за формулою
називається моментом інерції і -того елемента маси твердого тіла відносно нерухомої вісі ОО'. Момент інерції усього твердого тіла визначається за формулою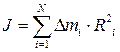 . (12)
. (12) . (13)
. (13) . (14)
. (14)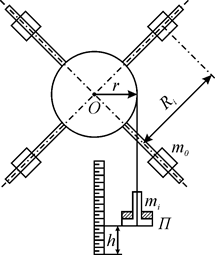
 Рис.9
Рис.9
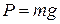 і сила натягу нитки
і сила натягу нитки 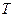 , яка діє вздовж нитки по дотичній до поверхні шківа маятника. Різниця цих двох сил, напрямлених в протилежні боки, і зумовлює абсолютну величину прискорення падаючого тіла a, тобто
, яка діє вздовж нитки по дотичній до поверхні шківа маятника. Різниця цих двох сил, напрямлених в протилежні боки, і зумовлює абсолютну величину прискорення падаючого тіла a, тобто
 (15)
(15)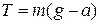 . (16)
. (16)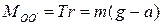 , (17)
, (17) , (18)
, (18)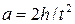 . (19)
. (19) . (20)
. (20) відносно осі ОО':
відносно осі ОО':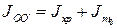 . (21)
. (21)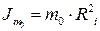 . Оскільки додаткових вантажів чотири, то остаточно момент інерції усіх додаткових вантажів можна розрахувати за формулою
. Оскільки додаткових вантажів чотири, то остаточно момент інерції усіх додаткових вантажів можна розрахувати за формулою . (22)
. (22)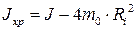 . (23)
. (23)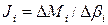 . (24)
. (24)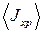 , а також абсолютну та відносну похибки.
, а також абсолютну та відносну похибки. ,с
,с
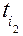 ,с
,с
 с,
с,
 ,с
,с




