
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм обробки результатів непрямих вимірюваньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Похибки посередніх вимірювань визначаються за похибками безпосередньо вимірюваних величин. Безпосередньо вимірювані величини
Розкладаючи праву частину виразу (7) у ряд Тейлора, матимемо:
Нехтуючи членами розкладу, які мають
Замінивши після диференціювання символ диференціалу
Отже абсолютна похибка функції одного аргументу дорівнює добутку похідної цієї функції на абсолютну похибку її аргументу. Для відносної похибки з (10) дістаємо:
Якщо посередньо вимірювана величина є функцією кількох аргументів
Цей вираз складається із суми частинних диференціалів, кожний з яких визначає ту частину похибки у величині функції, яка виникає через похибку кожного з аргументів
Абсолютна похибка будь якого аргументу може бути як додатною, так і від’ємною. У залежності від поєднання знаків усіх похибок аргументів за однакових усіх інших умов абсолютне значення абсолютної похибки
Наведеною вище формулою (14) зручно користуватися у тому випадку, якщо шукана величина є сумою або різницею результатів прямих вимірювань. Однак дуже часто виникає необхідність визначати похибку за формулами, які відображають складні функціональні залежності. Слід зазначити, що для величин, які виражені формулами, придатними для логарифмування, розрахунок похибок результатів непрямих вимірювань зручніше починати зі знаходження відносної похибки. Оскільки
У цю формулу замість частинних похідних від функції
Таким чином для того, щоб визначити похибку непрямих вимірювань рекомендується такий порядок операцій. Спочатку треба прологарифмувати вихідну функцію, тобто вихідну формулу, за якою розраховують значення досліджуваної фізичної величини, а потім продиференціювати одержаний вираз. Для цього треба спочатку визначити частинні похідні за кожним з аргументів
Приклади виведення формул для знаходження похибок непрямих вимірювань наведені у додатку №3. Наближені обчислення
Важливим питанням є те, скільки значущих цифр слід зберігати в результаті кожної дії. Точність обчислень результатів вимірювання має відповідати точності вимірювань. Виконувати обчислення з точністю, більшою ніж це дозволяють експериментальні дані, нераціонально і некоректно. Отже, обчислення, які виконуються при математичній обробці експериментальних результатів, отриманих у науковій чи навчальній лабораторії, є наближеними. Одержані числа можна округляти, тобто зменшувати кількість їх значущих цифр. Щоб округлити число до n значущих цифр, треба відкинути усі цифри, які стоять після n-го розряду. При цьому користуються такими правилами: якщо перша з цифр, які відкидають менша 5, то остання з тих цифр, які залишаються, не змінюється; якщо ж перша з цифр, які відкидають, більша або рівна 5, то остання цифра, з тих цифр, які зберігаються, збільшується на одиницю. Наприклад, округлення числа 7,192 до трьох значущих цифр дає число 7,19, до двох 7,2. Округлення числа 1681 до двох значущих цифр дає число У наближених обчисленнях записи 25,6 і 25,600 відрізняються один від одного. У числі 25,6 точні (правильні) лише цифри цілих і їхні десяті частини, а в числі 25,600 також соті і тисячні частини. Прийнято вважати, що k -та цифра наближеного числа а точною (правильною), якщо абсолютна похибка цього числа не перевищує половини одиниці k-го розряду цієї цифри. Всі цифри, які стоять лівіше від правильної, також правильні. У протилежному випадку цифру k-го розряду називають сумнівною. Сумнівною цифрою називають ту, яка стоїть безпосередньо за крайньою справа правильною цифрою. Цифри, які стоять справа від сумнівної цифри, називаються неправильними. Неправильні цифри повинні бути відкинуті шляхом округлення як у вихідних даних, так і у кінцевому результаті розрахунку. Всі правильні цифри числа, починаючи з першої зліва, відмінної від нуля, і включаючи першу сумнівну цифру, називаються значущими цифрами. Всі інші цифри називаються незначущими. Наприклад, у числі 0,0507 три значущих цифри; перші два нулі незначущі, нуль між п’ятіркою і семіркою – значущий. Записуючи остаточні результати наближених обчислень, незначущі цифри числа відкидають. У числі 2500 – чотири значущих цифри (нулі в числі 2500 – значущі цифри; точно відомо, що одиниць і десятків у числі 2500 немає). Запис 47200·103 або 0,47200·108 означає, що в числі 47 200 000 три останні цифри не значущі, а всі інші – значущі. Запис результатів вимірювання має відповідати також точності вимірювання. Наприклад, якщо товщина пластинки після обчислень становить 4,5568 мм при абсолютній похибці вимірювання 0,02 мм, то такий запис числа не відповідає теорії похибок вимірювання. Середнє арифметичне значення для товщини пластинки в цьому разі слід округлити до 4,56 мм. Взагалі при округленні наближеного або точного числа а до n значущих цифр за правилом доповнення число а замінюють числом Якщо з наближеними числами ще проводитимуться обчислення, то в них слід зберігати одну або дві сумнівні цифри. При виконанні математичних операцій над наближеними числами слід дотримуватись таких правил. Наближені числа треба округляти перед виконанням відповідних математичних операцій. Округляти числа слід за наведеним вище правилом до розряду найменш точного числа, залишаючи в числах одну або дві запасні цифри. Це дає змогу цілком правильно округлити кінцевий результат. У кінцевому результаті ці «запасні» цифри відкидають. При додаванні і відніманні наближених чисел кінцевий результат слід округляти так, щоб у ньому не було значущих цифр у тих розрядах, яких немає хоча б в одному з наближених чисел. Наприклад: 5,962 + 2,49 + 7,18376 + 6,1468 При множенні і діленні наближених чисел у кінцевому результаті слід залишати стільки значущих цифр, скільки їх є в наближеному числі з найменшою кількістю значущих цифр. Наприклад: 3,624·2,4·5,1127·3,62·2,4·5,11=8,688 При піднесенні до степеня в кінцевому результаті слід залишити стільки значущих цифр, скільки їх має наближене число, яке підноситься до степеня. Наприклад: (1,26)2=3,276 При добуванні коренів у кінцевому результаті слід залишити стільки значущих цифр, скільки їх має підкореневе наближене число. Наприклад: Знаходячи логарифм наближеного числа, потрібно брати з таблиць чи з дисплея мікрокалькулятора для мантиси стільки значущих цифр, скільки їх має це число. Наприклад: lg77,23 Правильне і обернене: число, яке знаходять за логарифмом, повинно мати стільки значущих цифр, скільки їх у мантиси (при довільній характеристиці). На основі викладеного вище, сформулюємо правила запису вимірювань і розрахунків, яких слід дотримуватись у навчальній лабораторії: 1. Остаточні результати вимірювань і розрахунків записують разом з їх абсолютною похибкою. 2. При запису похибок обмежуються однією (інколи двома значущими цифрами). Остання цифра результатів і остання цифра його абсолютної похибки повинні належати до одного і того ж самого десятинного розряду. Приклад правильного запису: 3..Якщо в похибці перша значуща цифра одиниця, то після неї зберігається ще одна, а в результаті дві сумнівні цифри. Приклад правильного запису: 4. Якщо у відповіді міститься множник виду 10n, то і у результаті, і у його абсолютній похибці він повинен бути однаковим. Приклад правильного запису: 5. Вимірювана величина і її абсолютна похибка виражаються в одних одиницях вимірювань. Приклад правильного запису: 6. Абсолютна похибку також треба округляти до однієї (іноді до двох) значущих цифр. Детальніше ознайомитись з методами обробки експериментальних результатів і розрахунку похибок можна за посібниками [7-9,11,19,39,40,43-46].
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 586; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.0.93 (0.008 с.) |

 вважатимемо аргументами, а посередньо вимірювані – функціями
вважатимемо аргументами, а посередньо вимірювані – функціями  . Розглянемо спочатку найпростіший випадок. Нехай
. Розглянемо спочатку найпростіший випадок. Нехай  , а абсолютна похибка прямого вимірювання величини X дорівнює
, а абсолютна похибка прямого вимірювання величини X дорівнює  . Очевидно, що
. Очевидно, що . (7)
. (7) (8)
(8) у степені, вищому за перший, дістаємо:
у степені, вищому за перший, дістаємо: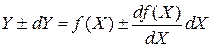 . (9)
. (9) на символ
на символ  , що позначає абсолютну похибку, матимемо:
, що позначає абсолютну похибку, матимемо: (10)
(10) . (11)
. (11)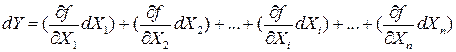 . (12)
. (12)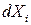 . При обчисленні частинної похідної
. При обчисленні частинної похідної  всі аргументи, крім
всі аргументи, крім  , вважаються сталими, а за величиною
, вважаються сталими, а за величиною  . (13)
. (13)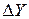 може мати різну величину. Для того, щоб бути впевненим у тому, що при самому несприятливому поєднанні знаків похибок аргументів
може мати різну величину. Для того, щоб бути впевненим у тому, що при самому несприятливому поєднанні знаків похибок аргументів  треба визначити максимальне значення
треба визначити максимальне значення  . (14)
. (14)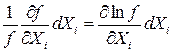 , то
, то . (15)
. (15)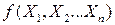 входять частинні похідні від логарифма цієї функції. Тому у тому випадку, коли залежність
входять частинні похідні від логарифма цієї функції. Тому у тому випадку, коли залежність  . (16)
. (16) усі відомі значення фізичних величин, які були одержані при проведенні прямих вимірювань чи взяті з таблиць, а також значення їх абсолютних похибок. Зверніть увагу на те, що у випадку проведення серії прямих вимірювань у цю формулу підставляють тільки середні значення величин, а розрахунок значення величини, одержаної у результаті проведення непрямого вимірювання, виконують тільки один раз. Після розрахунку відносної похибки
усі відомі значення фізичних величин, які були одержані при проведенні прямих вимірювань чи взяті з таблиць, а також значення їх абсолютних похибок. Зверніть увагу на те, що у випадку проведення серії прямих вимірювань у цю формулу підставляють тільки середні значення величин, а розрахунок значення величини, одержаної у результаті проведення непрямого вимірювання, виконують тільки один раз. Після розрахунку відносної похибки  (у відносних одиницях, а не у відсотках) треба визначити абсолютну похибку
(у відносних одиницях, а не у відсотках) треба визначити абсолютну похибку  і записати результат непрямого вимірювання фізичної величини
і записати результат непрямого вимірювання фізичної величини  . (17)
. (17)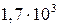 , а округлення числа 0,80214 – число 0,8. Абсолютна похибка округленого числа не перевищує половини одиниці останньої збереженої цифри. Це, зокрема, слід враховувати при округленні табличних даних та значень фізичних сталих, які беруть з довідкових таблиць.
, а округлення числа 0,80214 – число 0,8. Абсолютна похибка округленого числа не перевищує половини одиниці останньої збереженої цифри. Це, зокрема, слід враховувати при округленні табличних даних та значень фізичних сталих, які беруть з довідкових таблиць.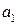 з n значущими цифрами так, щоб похибка округлення не перевищувала половини одиниці розряду, що зберігається.
з n значущими цифрами так, щоб похибка округлення не перевищувала половини одиниці розряду, що зберігається.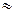 5,962+2,49+7,184 + +6,147=21,783
5,962+2,49+7,184 + +6,147=21,783  .
.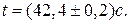 Приклад неправильного запису:
Приклад неправильного запису: 
 . Приклад неправильного запису:
. Приклад неправильного запису:  .
.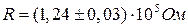 . Приклад неправильного запису:
. Приклад неправильного запису:  .
. . Приклад неправильного запису
. Приклад неправильного запису  .
.


