
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад обробки даних вимірювань.Содержание книги
Поиск на нашем сайте
Розглянемо опрацювання результатів при рівноточних вимірюваннях. Рівноточними вважаються почергові вимірювання незмінними засобами, у незмінних умовах, незмінним вимірювачем. Якщо дисперсія (розсіювання) випадкових похибок заздалегідь невідомі, то: - за оцінку результату вимірювання беруть середнє значення - оцінюють вибіркову дисперсію випадкових похибок результатів спостережень та обчислюють середнє квадратичне відхилення результату спостереження (похибок результатів спостережень)
- перевіряють найбільш відхилені від середнього значення результати спостережень на можливість їх спотворення грубими похибками чи наявність промахів. При потребі такі результати відкидають і повторно виконують перші два пункти при скороченій (на кількість відкинутих результатів) виборці; - оцінюють дисперсію випадкової похибки очікуваного результату вимірювання (тобто дисперсію середнього арифметичного значення результату), яка в N раз менша за оцінку дисперсії окремих результатів спостережень та обчислюють середнє квадратичне відхилення результату вимірювання (СКВ випадкової похибки результату вимірювання)
- оцінюють довірчі межі похибки (невизначеність (або непевність) результату вимірювання)
де Перевірку гіпотези про те, що результати спостережень належать до нормального розподілу, проводять з рівнем значимості q = 0,01...0,10. Конкретні значення рівнів значимості повинні бути зазначені в конкретній методиці виконання вимірювань. - При кількості результатів спостережень N >50 для перевірки належності їх до нормального розподілу використовують методику зазначену у ГОСТ 11.006-74. - При кількості результатів спостережень 50> N >15 для перевірки належності їх до нормального розподілу використовують складений критерій, який наведено нижче. - При кількості результатів спостережень N
При кількості результатів спостереження 50> N >15 нормальність їхнього розподілу перевіряють за допомогою складного критерію d i m. Обчислюють відносну величину d (відношення величини розсіювання результатів до СКВ цих результатів)
де σ* – зміщена оцінка середнього квадратичного відхилення результатів, що обчислюється за формулою:
Результати спостережень групи можна вважати розподіленими нормально, якщо
де q – заздалегідь обраний рівень значимості критерію (прийняти q = 0,02). Вважається, що розподіл відносної величини d подібний до розподілу Гауса. Квантúль – є мірою розсіювання (за ймовірністю) випадкової величини. Квантиль порядку Р (Р – це, як ми пам’ятаємо, ймовірність) – це таке значення випадкової величини для якого функція розподілу дорівнює Відповідно, квантилі 1-q/2 та q/2 – це значення випадкових величин (хі), для яких функція розподілу F(x) набуває значень 1-q/2 та q/2.
Рис. 3.3. Квантилі та інтерквантильна ширина розподілу.
Таблиця 3.3 Значення квантиля d- розподілу
Після перевірки даної умови приступають до аналізу другого критерію т (критична кількість відхилень), який являє собою кількість різниць Δ*, які перевершили значення:
де zР – квантиль Лапласа, який відповідає ймовірності Р.
Δ*= | xi -
Значення Р вибирають з табл. 3.4 за рівнем значимості q та N.
Таблиця 3.4 Значення Р для обчислення zР й критичної кількості відхилень т.
Таблиця 3.5 Значення квантилій Лапласа
У тому разі, якщо хоча б один з критеріїв не виконується, вважають, що розподіл результатів не відповідає нормальному. Після перевірки гіпотези про те, що результати спостережень належать до нормального розподілу можна приступити до запису одержаних результатів. Результати вимірювання записують у стандартній формі:
Х =
Для зменшення впливу випадкових похибок на результати вимірювань можна збільшити кількість вимірювань, але це збільшення має бути обґрунтованим. Для цього знаходять середнє значення з результатів спостережень
Порядок виконання роботи. 4.1. Згідно з номером варіанта одержати вихідні дані (результати попередніх вимірювань). 4.2. Зробити попередній аналіз вихідних даних. 4.3. Обробити дані вимірювань. 4.4. Оформити протокол, дати висновок. Допоміжні матеріали. 5.1. ГОСТ 8.207- 90 „Методы обработки результатов измерений.” 6. Контрольні питання. 6.1. Яким чином виникає статистична помилка? 6.2. Яким чином виникає систематична помилка? 6.3. Яким чином усувають вплив статистичної помилки? 6.4. Як визначають можливі промахи у результатах? 6.5. Як перевіряється належність результатів вимірювань до нормального закону розподілу результатів? 6.6. Як не змінюючи умов вимірювання підвищити точність вимірювань? Лабораторна робота № 4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.69.25 (0.008 с.) |

 ;
;


 – коефіцієнт, взятий з таблиці для розподілу Ст'юдента, що залежить від так званої кількості ступенів свободи f яка для вирішення наших завдань завжди дорівнюватиме N - 1, та наперед заданої довірчої ймовірності Р (табл. 3.1).
– коефіцієнт, взятий з таблиці для розподілу Ст'юдента, що залежить від так званої кількості ступенів свободи f яка для вирішення наших завдань завжди дорівнюватиме N - 1, та наперед заданої довірчої ймовірності Р (табл. 3.1). 15 належність їх до нормального розподілу не перевіряють. При цьому знаходження довірчих меж випадкової похибки результату вимірювання за методикою, передбаченою стандартом, можливо в тому випадку, якщо заздалегідь відомо, що результати спостережень належать до нормального розподілу.
15 належність їх до нормального розподілу не перевіряють. При цьому знаходження довірчих меж випадкової похибки результату вимірювання за методикою, передбаченою стандартом, можливо в тому випадку, якщо заздалегідь відомо, що результати спостережень належать до нормального розподілу.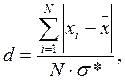


 й
й  – квантилі d- розподілу (розподілу відносного значення розсіювання результатів), одержувані зa табл. 3.3 по N, 1-q/2 та q/2;
– квантилі d- розподілу (розподілу відносного значення розсіювання результатів), одержувані зa табл. 3.3 по N, 1-q/2 та q/2; .
.

 менший за розкид окремого результату спостереження, для зменшення впливу випадкової похибки у N раз необхідно здійснити N2 спостережень.
менший за розкид окремого результату спостереження, для зменшення впливу випадкової похибки у N раз необхідно здійснити N2 спостережень.


