
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оцінка результатів та помилки вимірювань.Содержание книги
Поиск на нашем сайте
Метою кожного вимірювання є визначення значення деякої величини. Однак через різні неточності процесу вимірювання результати вимірювань у загальному випадку відрізняються від шуканого точного значення. При оцінці результатів вимірювання зазвичай виходять із того, що вимірювання можна повторити багаторазово. Умови проведення вимірювань при цьому не повинні змінюватися. Досвід показує, що будь-яке вимірювання, як би акуратно воно не проводився, не може бути зовсім без помилок. У наукових дослідженнях слово „помилка” означає неминучу похибку, якою супроводжуються всі вимірювання. Помилка вимірювання характеризує точність, з якої виконано вимірювання. Помилки вимірювань обумовлені більшою кількістю різноманітних причин. У деяких випадках вдається виділити причини цих помилок і внести необхідне виправлення в результат вимірювань. Іншою причиною похибок експерименту може бути неточність приладу, що вимірює, часовий інтервал спостереження. Для того щоб максимально уникнути таких помилок у наукових експериментах намагаються використовувати спеціально калібровані прилади. Прийнято говорити, що кожна з таких причин викликає систематичну помилку вимірювань. Як тільки систематичні помилки виявлені і їхні величини розраховані, вони можуть бути усунуті внесенням відповідних виправлень у результати вимірювань. Однак необхідно пам'ятати, що загальна помилка кожного результату вимірювання залишається невідомою, тому що мова йде не про виділення із загальної помилки спостереження деякої її частини у вигляді систематичної помилки, а лише про введення виправлень на ті фактори, які вдалося виявити в процесі аналізу результатів експерименту. Правильна оцінка систематичних помилок у значній мірі залежить від досвіду експериментатора і його здатності критично дивитися на отримані результати. Поряд із систематичними помилками існують й іншого типу помилки – статистичні. Статистичні помилки є непереборними – їх не можна виключити в кожному з результатів вимірювань. Але за допомогою методів теорії імовірності можна врахувати їхній вплив на оцінку дійсного значення вимірюваної величини, що дозволяє визначити значення вимірюваної величини зі значно меншою помилкою ніж помилки окремих вимірювань. Урахування впливу статистичних помилок засновано на знанні законів їхнього розподілу, тому що статистичні помилки вимірювання характеризуються певним законом розподілу. Існування такого закону можна виявити, повторюючи багато разів у незмінних умовах вимірювання деякої величини.
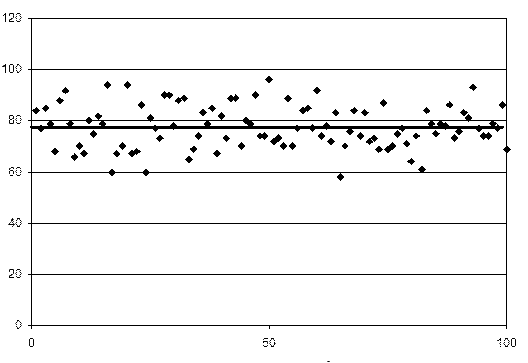
Розглянемо експеримент під час якого було виконано 100 незалежних вимірювань деякої фізичної величини у незмінних умовах. Видно, що в кожному окремому вимірюванні реєструється якась кількість випадкових відліків (результатів вимірювань за показами вимірювального пристрою), ніяк не пов'язаних з результатами попередніх вимірювань.
Рис. 3.1. Результати вимірювань деякої фізичної величини, як функція номера вимірювання.
На рис. 3.1 показані результати х цих вимірювань, як функція номера вимірювання N. Видно, що вони сконцентровані поблизу деякої величини
У нашому випадку N = 100, Очевидно, що усереднена по N вимірюваннях величина Незважаючи на те, що в середньому всі результати вимірювань концентруються поблизу Яким саме чином різні значення хі розміщені навколо Якщо вважати, що
Щоб спробувати оцінити вірогідність результатів вимірювань, здавалося, можна було б підійти аналогічно й усереднити величини Δ х. Однак, значення усередненої величини
Щоб обійти цю неприємність, у статистиці використовують іншу величину, яка дорівнює квадрату відхилення, усередненому за всяким значенням цієї величини, що називається дисперсією (або варіацією) й позначається символом D(х) (або Var(х)). Квадратний корінь із дисперсії називається середнім квадратичним (або середньоквадратичним) відхиленням:
Середнє квадратичне відхилення Для визначення дисперсії підносять до квадрату усі відхилення від середньої величини й потім ці величини усереднюють за кількістю повторних вимірювань:
Наведені формули є справедливими у тому разі, коли кількість вимірювань не обмежено велика. На практиці, при обмеженій (невеликій) кількості вимірювань, коли розподіл результатів вимірювань відносно „істинного результату” відрізняється від симетричного й не співпадають значення „істинного” й середнього арифметичного результатів, формулу дисперсії (3.4) „модифікують” у такий спосіб:
Ця величина є практичною оцінкою розподілу результатів вимірювання – дисперсією вимірювання. Визначена за формулою (3.5) дисперсія трохи більша чим за формулою (3.4), це частково компенсує помилку у вимірюваннях у тому випадку, коли число вимірювань мале (N ≤ 20…30). При збільшенні N співвідношення (3.4) і (3.5) приводять практично до однакових результатів. Дисперсія вимірювань являє собою усереднене середньоквадратичне відхилення результатів окремих вимірювань х 1, х 2, … хN від середнього значення Середньою квадратичною похибкою спостереження називається величина
Для того, щоб узнати наскільки може відхилятися від дійсного значення х його середнє арифметичне, отримане для N повторних рівноточних вимірювань, розраховують середню квадратичну похибку середнього арифметичного. За даними багаторазових статистичних досліджень визначено, що середня квадратична похибка середнього арифметичного дорівнює середній квадратичній похибці окремого результату вимірювань σх, діленої на корінь квадратний із кількості вимірювань N, тобто
Це фундаментальний закон зростання точності при рості числа спостережень. Нехай Р означає ймовірність того, що результат вимірювань відрізняється від дійсного на величину, не більшу, ніж Δх. Імовірність Р у цьому випадку зветься довірчою ймовірністю, а інтервал значень вимірюваної величини від - Δх до + Δх називається довірчим інтервалом. Визначимо довірчий інтервал. Чим більшим буде встановлений цей інтервал, тим з більшою ймовірністю хдійсне попадає в цей інтервал. З іншого боку, більш широкий інтервал подає меншу інформацію щодо величини хдійсне. Якщо обмежитися обліком тільки випадкових похибок, то при невеликій кількості вимірювань N для рівня довірчої ймовірності Р напівширина довірчого інтервалу дорівнює
де t – коефіцієнт Ст'юдента. Зміст понять „довірчий інтервал” й „довірча ймовірність” полягає в наступному: нехай Р = 95, тоді можна стверджувати з надійністю 95 %, що дійсне значення величини хдійсне не відрізняється від оцінки Таблиця 3.1 Значення коефіцієнтів Ст'юдента
Примітка: f – кількість ступенів свободи, f = N-1.
Щоб остаточно встановити межі довірчого інтервалу необхідно розширити його з урахуванням систематичної похибки Δхсист. Систематична похибка, як правило, зазначена в паспорті або на шкалі приладу, а в найпростіших випадках може бути прийнята рівній половині ціни розподілу молодшого розряду шкали. Звичайно сумарна похибка визначається як корінь квадратний із суми квадратів випадкової й систематичної похибок:
3.2. Виявлення й виключення грубих похибок (промахів) вимірювань. Грубі похибки вимірювань (промахи) можуть сильно спотворити результати вимірювань, тому їхнє виключення із серії дослідів вимірювань обов'язкове. Звичайно вони відразу видні в ряді отриманих результатів, але в кожному конкретному випадку це необхідно довести. Існує ряд критеріїв для оцінки промахів. Критерій 3σ. Вважається, що результат, що виникає з імовірністю ≤ 0,3 %, малоймовірний і його можна кваліфікувати промахом, тобто сумнівний результат xj відкидається, якщо
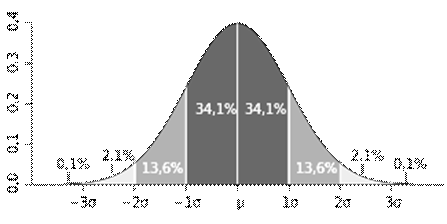
Якщо розподіл результатів вимірювань відповідає нормальному закону (розподіл Гауса), то приблизно 99,73 % усіх результатів вимірювань опиняться у межах інтервалу від – 3σ до + 3σ.
Рис. 3.2. Графік щільності ймовірності нормального розподілу та процент потрапляння випадкової величини на відрізки, які дорівнюють σх.
На рис. 3.2 µ – математично очікуване значення результату вимірювань (µ = Величини
Якщо N < 20, доцільно застосовувати критерій Романовського. При цьому обчислюють відношення
отримане значення β порівнюють із табличним βт – при обираному рівні значимості Р по табл. 3.2. Таблиця 3.2 Рівень значимості βт = f(N)
Зазвичай вибирають Р = 1... 5 %, і якщо β > βт, то результат відкидають.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1087; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.012 с.) |

 . Середнє число часток
. Середнє число часток 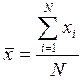
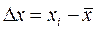 .
.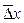 при нормальному розподілі результатів вимірювань буде наближатися до нуля:
при нормальному розподілі результатів вимірювань буде наближатися до нуля: (3.2)
(3.2)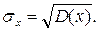 (3.3)
(3.3) х характеризує середню похибку окремих вимірювань х1, х2,... хі,...хk і вказує інтервал у якому із високою ймовірністю будуть спостерігатися результати вимірювань [– sx...
х характеризує середню похибку окремих вимірювань х1, х2,... хі,...хk і вказує інтервал у якому із високою ймовірністю будуть спостерігатися результати вимірювань [– sx... 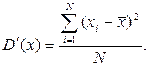 (3.4)
(3.4)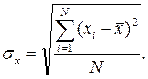
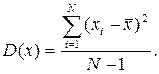


 (3.8)
(3.8)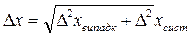 .
.
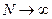 ).
).



