
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика обробки результатів двох серій вимірювань.Содержание книги
Поиск на нашем сайте
Перевірка гіпотези про наявність систематичної складової похибки. 1. Мета роботи.
1.1. Вивчити методологію обробки результатів двох серій вимірювань. 1.2. Освоїти методику визначення наявності систематичної складової похибки. 1.3. Придбати навики обробки результатів двох серій вимірювань.
Зміст роботи. 2.1. Ознайомитись з теорією обробки результатів двох серій вимірювань та визначення наявності систематичної складової похибки. 2.2. Визначити присутність та вагомість систематичної похибки у результатах вимірювання. 2.3. Зробити висновки.
Теоретичні відомості. У практиці вимірювань часто буває необхідно виявити наявність систематичної похибки результатів спостережень, обумовленої впливом якого-небудь постійно діючого чинника. У такому разі проводять багаторазові вимірювання (загальною кількістю N), розбивають їх на достатнє число m серій, кожна з яких відповідає певним (хай невідомим, але різним) значенням впливаючого чинника. Чинниками, по яких виконується об'єднання результатів в серії, можуть бути зовнішніми умовами, часовою послідовністю і тому подібне. Після розділення вимірювань на серії в кожній з них по відомих критеріях встановлюють відповідність результатів нормальному закону. Окрім цього, перевіряють однорідність серій вимірювань, виконаних в однакових умовах, за допомогою критеріїв Стьюдента t й Фішера F. Розрахункове значення критерію Стьюдента tе визначається за формулою:
де
N 1 та N 2 – об’єми серій вимірювань, що перевіряються, N 1 ≠ N 2.
Якщо N 1 = N 2 = N, то формула приймає вигляд
Розрахункове значення критерію Фішера визначається за формулою:
Обчислені значення tе і Fе порівнюють з табличними значеннями tT[Р = 0,95; f = N1+N2 – 2] та FT[Р = 0,95; f 1 = N1 – 1; f 2 = N2 – 1] відповідно. Якщо виконуються нерівності FT> Fe q tT> te, то гіпотеза про рівність дисперсій і середніх значень в серіях, що перевіряються, не відкидається. В цьому випадку передбачається, що розсіювання результатів в межах кожної серії і між серіями, виконаними в однакових умовах, відображає лише випадкові похибки.
Порядок виконання роботи. 4.1. Згідно з номером варіанта одержати вихідні дані для розрахунків (результати попередніх вимірювань). 4.2. Зробити попередній аналіз вихідних даних, вилучити за необхідністю грубі помилки. 4.3. Обробити дані вимірювань. 4.4. Оформити протокол, зробити висновки.
5. Контрольні питання. 5.1. Які можуть бути причини виникнення систематичних похибок? 5.2. Яким чином визначається наявність у результатах вимірювань систематичної похибки? 5.3. Як усуваються або компенсуються систематичні похибки? Лабораторна робота № 5 Визначення похибки одноразових непрямих вимірювань 1. Мета роботи: ознайомитися з правилами обчислення похибок непрямих одноразових вимірювань, а також із діями з наближеними числами. Зміст роботи. 2.1. Ознайомитись з теорією визначення похибки одноразових непрямих вимірювань. 2.2. Вивчити правила обчислення похибок непрямих одноразових вимірювань. 2.3. Зробити відповідні висновки.
Теоретичні відомості. Непрямі вимірювання – це вимірювання, при яких значення вимірюваної величини знаходять шляхом обчислень на підставі відомої залежності між цією величиною й іншими величинами, отриманими прямими вимірюваннями. У загальному випадку залежність, що зв'язує вимірювану величину Y і величини Х1, Х2...,Хп, можна представити у вигляді: Y = F(X1, X2,...Xn). Такі вимірювання дуже поширені і мають велике значення у метрологічній практиці. Наприклад, вимірювання щільності речовини p вимагає вимірювання маси m і об'єму V за допомогою прямих вимірювань, а потім обчислення за формулою p = тV. Окрім непрямих вимірювань, пошук залежності між величинами здійснюється проведенням сукупних і спільних вимірювань. Спільними називаються вимірювання, що проводяться одночасно для двох або більше неоднорідних величин для встановлення залежності між ними. Сукупними називаються вимірювання, які проводяться одночасно для декількох однорідних величин, коли їх шукані значення знаходять вирішенням системи рівнянь, що отримуються при різних поєднаннях цих величин (Приклад: вирішення системи рівнянь електричного ланцюга за законом Кірхгофа). Оцінка похибок непрямих вимірювань включає два етапи. Спочатку необхідно оцінити похибки у величинах, отриманих прямими вимірюваннями, а потім визначити, як ці похибки трансформуються в процесі обчислень і відбиваються на кінцевому результаті. Дії з величинами і їхніми похибками, які найбільш часто зустрічаються, приведені в табл. 5.1.
При остаточному записі результатів непрямих вимірювань необхідно враховувати наступні правила: 1) результат вимірювання округляється до того ж десяткового знаку, яким закінчується закруглене значення абсолютної похибки. Якщо десятковий дріб в числовому значенні результату вимірювань закінчується нулями, то нулі відкидаються до того розряду, який відповідає розряду числового значення похибки; 2) якщо цифра старшого з відкиданих розрядів менше п'яти, то останні цифри числа не змінюються. Зайві цифри в цілих числах замінюються нулями, а в десяткових дробах відкидаються; 3) якщо цифра старшого з відкиданих розрядів більше або рівна п'яти, але за нею слідують відмінні від нуля цифри, то останню цифру, що залишається, збільшують на одиницю; 4) якщо відкидана цифра дорівнює п'яти, а наступні за нею цифри невідомі або дорівнюють нулю, то останню цифру числа, що зберігається, не змінюють, якщо вона парна, і збільшують на одиницю, якщо вона непарна; 5) округлення виконується лише в остаточній відповіді, а всі проміжні обчислення проводять з одним - двома зайвими знаками.
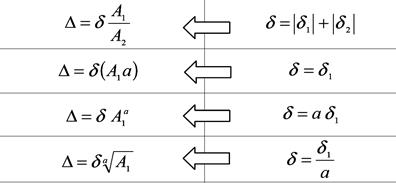
Таблиця 5.1. Вираження для обчислення граничної похибки результату при різних діях з величинами
Примітка: у таблиці стрілками показана черговість обчислення похибки: для арифметичних дій – від абсолютних до відносних похибок, а для алгебраїчних дій – навпаки.
Порядок виконання роботи. 4.1. Визначити похибку непрямих вимірювань лінійної щільності пряжі. Для цього необхідно: - визначити довжину L відрізання пряжі, користуючись метровою лінійкою з ціною поділки С = ∆L = 5 мм, при цьому її дійсне значення Lд буде дорівнювати
- визначити масу т відрізання пряжі на торсіонних вагах з ціною поділки С= ∆т = 1 мг міліграм, при цьому її дійсне значення тд буде дорівнювати
- розрахувати лінійну щільність Т [текс] пряжі за формулою:
де m – маса відрізання, мг; L – довжина відрізання, мм; При цьому дійсна лінійна щільність Тд буде дорівнювати
- прийняти абсолютну похибку вимірювання маси Д т і довжини Д L, рівній ціні ділення відповідного засобу вимірювання; - визначити відносні похибки вимірювань маси і довжини за формулою:
δ = Δ / X
причому замість дійсного значення узяти фактично виміряне значення; - обчислити відносну і абсолютну похибки непрямого вимірювання по формулах рядка 4 таблиці. 1; - записати підсумковий результат, використовуючи правила округлення, у вигляді
Тд= Т ± Δ.
4.2. Оформити протокол, зробити висновки.
5. Контрольні питання. 5.1. Що називається непрямими і прямими вимірюваннями? 5.2. Які вимірювання називають спільними, а які сукупними, і у чому різниця? 5.3. Охарактеризуйте основні етапи визначення похибки для непрямих вимірювань. 5.4. У яких випадках підсумовуються абсолютні похибки, а в яких відносні? Лабораторна робота 6.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.92 (0.007 с.) |

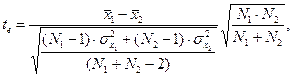
 1 та
1 та 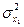 та
та  – дисперсії серій вимірювань, що перевіряються;
– дисперсії серій вимірювань, що перевіряються;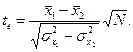
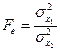 при
при 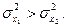

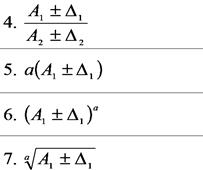

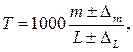 (5.4)
(5.4)


