
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математична обробка результатів експериментуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для того, щоб мати можливість судити за певною ознакою генеральної сукупності по даних вибірки, необхідно, щоб вибірка була репрезентативною, тобто представницькою. Випробуванням підлягає не вся партія текстильного матеріалу, а лише певна її частина, внаслідок чого виникають похибки вибірки. Для обчислення, вільних характеристик, які б надавали б більш повну уяву про типову величину властивості, яка вивчається, всієї партії матеріалу, обчислюють середнє арифметичне значення та коефіцієнт нерівноти. Середнє арифметичне значення (
де п – це число вимірювань (об'єм вибірки); Хі – окремі результати вимірювань. Коефіцієнт нерівноти у більшості випадків визначається за стандартною формулою:
де Xм – середнє арифметичне значення з результатів випробувань менших за числове значення загальної середнє арифметичної; п – загальна кількість випробувань; п1 – кількість випробувань менших за числове значення загальної середньої арифметичної. Підрахунок Н виконують з точністю до 0,01 і округлюють до 0,1%. Приклад 1 При визначенні тонини швейних шовкових ниток № 16 (умовний номер 18), що намотані на бобіни, отримали наступні результати (табл. 12.1). Отриманий результат порівнюють з нормативом стандарту на даний вид шовкових ниток при визначенні сортності та надають оцінку якості. Вільні характеристики, що обчислюються за результатами випробувань частини партії, завжди будуть відрізнятися від вільних характеристик, отриманих при випробуванні всієї партії матеріалу. Досліджувати всю партію матеріалу не можливо з двох причин. По-перше, під час визначення, наприклад, характеристик при розриванні таке випробування призвело б до псування всієї партії матеріалу, по-друге, якщо партія матеріалу повністю зберігається, її повний аналіз буде досить тривалим і результати його не зможуть бути використані у оперативній роботі.
Таблиця 12.1 Тонина швейних шовкових ниток (умовний номер 18), отримана у результаті вимірів
Внаслідок наведених причин випробується не вся партія матеріалу, а лише її певна частина, тому похибок вибірки уникнути або усунути їх не можливо, але вони повинні бути враховані при використанні результатів випробувань спеціальними методами математичної статистики. Така обробка результатів проводиться зазвичай не при виконанні стандартних лабораторних випробувань, а при виконанні науково-дослідних робіт. У цих випадках математична статистика рекомендує обчислювати наступні характеристики: середнє квадратичне відхилення σ, коефіцієнт варіації С, середню похибку середнє арифметичного т та коефіцієнта варіації тс, гарантійні похибки вибірки середнє арифметичного тг та коефіцієнту варіації Середнє квадратичне відхилення обчислюється за формулою:
3начення σмає ту ж розмірність, що й окремі випробування. Для розрахунку коефіцієнту варіації використовують таку формулу:
При нормальному розподілі та великому числу (≥100) випробувань матеріалу можна орієнтовно вважати, що: С = 1,25Н. (12.5) Коефіцієнт нерівноти Н за числовим значенням завжди менше ніж коефіцієнт варіації С, оскільки при підрахунку враховуються похибки вибірки. Коефіцієнт варіації обчислюють з точністю 0,1%. Він має те ж саме значеннєве значення, що й коефіцієнт нерівноти. Обидва ці показники характеризують рівномірність текстильних матеріалів по показникам будови та фізико-механічним властивостям. Чим менше числове значення С або Н, тим більш рівномірним є матеріал за будовою та властивостями, тим вище його якість. Слід вважати, що характеристики нерівномірності властивостей матеріалу коефіцієнт варіації застосовувати не рекомендується, якщо окремі результати Випробувань коливаються коло нуля. Коефіцієнт варіації С характеризує ступінь розкиду тієї чи іншої властивості, тобто в якомусь ступені показники даної властивості матеріалу відхиляються від середнього. Якщо С < 5%, матеріал рівномірний та однорідний за досліджувальною властивістю; якщо С = 5÷10% – це означає, що властивості матеріалу досить рівномірні; С = 10÷15%, то це вказує на нерівномірність даної властивості матеріалу; якщо С > 15%, це означає, що показники властивості сильно розкидані. Середня похибка середнього арифметичного по виборці визначається за формулою: де α – нормоване відхилення, яке обирається в залежності від числа випробувань п: п® 5 10 15 20 а® 2,9 2,3 2,2 2,1 Розмірність т така ж, як і розмірність σ. Середня похибка коефіцієнта варіації визначається за формулою:
де α – коефіцієнт, що характеризує точність випробувань; п – число випробувань. Гарантійні похибки вибірки тг та Згідно теорії математичної статистики, при різноманітних значеннях αймовірність на кожне випробування різна: Значення αЙмовірність 1 0,680 2 0,954 3 0,997 В оцінці точності результатів випробувань, Знаючи гарантійну помилку коефіцієнта варіації, керуються наступними критеріями: Гарантійна похибка Менше 2.......................... Хороший Від 2 до 10 Середній Більше 10 Низький При низькому результаті випробувань необхідно збільшувати число випробувань. З формули (12.6) видно, що точність випробувань прямо пропорційна рівномірності будови або властивостям досліджуваного матеріалу з ймовірністю в залежності від числового значення αй обернено пропорційна кореню квадратному з подвійного числа випробувань. Рівномірність будови або властивостей досліджуваного матеріалу змінити не -і-можливо, оскільки вона відображає його природні властивості; тому точність аналізу можна підвищити лише шляхом збільшення кількості випробувань. Знаючи значення С та ймовірність значення α, можна задатися потрібною точністю аналізу, та підрахувати, яку кількість випробувань необхідно провести для цієї мети, за формулою (12.8).
Якщо розрахункове значення п менше за експериментальне, то можна говорити, що для певної мети достатня кількість експериментальних випробувань, якщо п розрахункове значно перебільшує експериментальне, то експеримент слід повторити. Дійсне середнє арифметичне значення з ймовірністю від числового і значення а визначається за формулами:
або Дійсний коефіцієнт варіації з ймовірністю від числового значення αвизначається за формулами:
або Приклад 2. Необхідно визначити міцність бавовняних глянсових ниток у три складання марки Екстра, торгового номеру З0. Для спрощення числового прикладу кількість випробувань була узята не 100, як це потрібно робити згідно стандарту, а лише 25. Знайшли значення Хi та Загальна сума результатів випробувань
Так, при даній нерівноті за міцністю ниток для отримання, наприклад,
Дійсне середнє арифметичне, що визначається за формулою (3.8), складатиме: Дійсне значення коефіцієнту варіації, що визначається за формулою (3.9), дорівнює: Отже, при проведенні обробки результатів випробувань зразків партії методом математичної статистики з ймовірністю при α=2 теоретично встановлено, що якщо б випробувалась уся партія ниток, то середня міцність їх у 954 випадках на кожні 1000 знаходилася б у межах 1442,6 ÷ 1597,4 сН і лише у 46 випадках була б більше або менше цих величин.
Таблиця 12.1 Результати визначення міцності бавовняних ниток, сН
При цьому рівномірність ниток за міцністю, яка виражається коефіцієнтом варіації, також на кожні 1000 випробувань в 954 випадках знаходився б у межах 8,9÷15.9°/о і лише у 46 випадках була б більше або менше цих величин. Таким чином, обробка результатів випробувань методом математичної статистики надає можливість розповсюджувати з відомою точністю результати випробувань, отриманих по зразкам, на усю партію текстильного матеріалу. НОРМАЛЬНИЙ ЗАКОН РОЗПОДІЛУ Випадкові похибки вимірювань найчастіше підкоряються нормальному законові розподілу (закон Гауса). Щільність нормального розподілу має наступний вигляд:
де z – випадкова похибка; σ (σ>0) – параметр, який характеризує точність вимірювань. Графік щільності розподілу ймовірностей, або крива розподілу, при зменшенні параметра σ (рис. 12.1) стискається вздовж осі О z та витягається вздовж осі Р|z|. Отже, чим менше σ, тим швидше спадає щільність розподілу Р(z) зі зростанням |z|. Ймовірність попадання в інтервал (-z1, z1) графічно зображується площею, яка відповідає криволінійній трапеції під кривою розподілу ймовірностей. Зокрема, ймовірність попадання в симетричний інтервал (-z1, z1, при z 1>0) зображується площею фігури, що заштрихована на рис. 12.2. Звідси випливає, що чим σ менше, тим менше розкид похибок поблизу нуля. Ймовірність попадання випадкової похибки в симетричний інтервал (-z1, z1) при нормальному розподілі обчислюють за формулою:
де функція
Функція Ф(t) називається інтегралом ймовірностей, позитивних значень аргументу приведені в додатку А.
Рис. 12.1. - Криві нормального розподілу Рис. 12.2 — Ймовірність попадання при різних значеннях σ випадкової помилки в інтервал ((-z1, z1) Ймовірність попадання випадкової похибки в будь-який інтервал при нормальному розподілі обчислюють за формулою:
Ймовірність того, що випадкова похибка виходить за межі ±tσ(t > 0), складає:
Якщо випадкові похибки г мають нормальний закон розподілу з щільністю, яка виражена формулою (12.1), то розподіл результатів виміру х=a+z має щільність:
яка тільки зсуванням на величину а відрізняється від щільності, що обумовлена формулою (12.1). Це і закон розподілу має назву загального нормального закону з центром у точці а. При цьому щільність може бути записана як φ0,σ (z). Для випадкових похибок завжди передбачається, що центр їх розподілу дорівнює нулю. Параметр σ є середньоквадратичним відхиленням вимірювання (стандартною похибкою), а σ2 – дисперсією відхилення. Крім цих показників застосовуються ще й інші показники точності вимірів, співвідношення між якими при нормальному розподілі похибок є такими: – ймовірна похибка: ρ= 0,6745σ; 2Ф(ρ)=0,5; (12.19) – середня абсолютна похибка:
– міра точності:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1036; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 ) обчислюється шляхом складання усіх окремих результатів випробувань (Хі) та діленням їх суми (å) на загальне число випробувань (п), та визначається за формулою:
) обчислюється шляхом складання усіх окремих результатів випробувань (Хі) та діленням їх суми (å) на загальне число випробувань (п), та визначається за формулою: (12.1)
(12.1)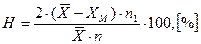 (12.2)
(12.2)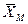 = 15,4. Підставляючи результати обчислень у формулу (12.2), отримаємо:
= 15,4. Підставляючи результати обчислень у формулу (12.2), отримаємо:  .
.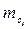 , дійсне арифметичне середнє арифметичне значення Мг та коефіцієнту варіації Сг. середнє квадратичне відхилення та похибки обчислюються за різними формулами в залежності від методу добору проб з партії матеріалу. Застосування цих формул у кожному випадку забезпечує велику точність обробки результатів вимірювань. Найчастіше застосовують наступні формули.
, дійсне арифметичне середнє арифметичне значення Мг та коефіцієнту варіації Сг. середнє квадратичне відхилення та похибки обчислюються за різними формулами в залежності від методу добору проб з партії матеріалу. Застосування цих формул у кожному випадку забезпечує велику точність обробки результатів вимірювань. Найчастіше застосовують наступні формули. (12.3)
(12.3) (12.4)
(12.4)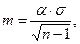 (12.6)
(12.6)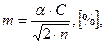 (12.7)
(12.7) (12.8)
(12.8) (12.9)
(12.9)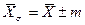 (12.10)
(12.10) (12.11)
(12.11) (12.12)
(12.12)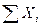 складає 38000. Середнє арифметичне
складає 38000. Середнє арифметичне  . Підставляючи в формулу (3.2) значення окремих показників, маємо:
. Підставляючи в формулу (3.2) значення окремих показників, маємо:



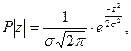 (12.13)
(12.13) (12.14)
(12.14) (12.15)
(12.15)
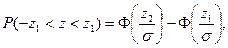 (12.16)
(12.16)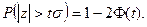 (12.17)
(12.17)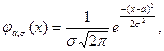 (12.18)
(12.18) (12.20)
(12.20) (12.21)
(12.21)


