
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для побудови та дослідження математичних моделейСодержание книги
Поиск на нашем сайте Мета роботи Засвоїти методику планування експерименту для отримання моделей технологічних систем і навчитися їх досліджувати з метою удосконалення або розробки їх підсистем. Прилади і матеріали: персональний комп’ютер типу ІВМ PС,програма PLAN2.exe. ТЕОРЕТИЧНІ ВІДОМОСТІ Розвиток математичної статистики та її широке проникнення в техніку та в різноманітні сфери науки дали можливість створити математичну теорію експерименту. За допомогою цієї теорії розв’язуються різноманітні питання експериментальних досліджень, в тому числі математичне планування експерименту, оптимізації технологічних процесів та інше. Сутність методу полягає в тому, що на основі обмеженої кількості проведених експериментів встановлюється кореляційна залежність між показниками процесу та вихідними параметрами продукції. Останнім часом отримали широкий розвиток математичні моделі, якими є рівняння, що виражають залежність параметра оптимізації (Y) від факторів (х 1, х 2, …, х k):
Наведена функція отримала назву функції відгуку – функція, яка характеризує процес, що досліджується. При оптимізації створюваних, або вже існуючих складних технологічних процесів, при дослідженні нових матеріалів необхідно завжди прагнути, щоб при найменших витратах матеріальних засобів та часу отримати найбільш повну та точну інформацію про вплив кожного досліджуваного фактора на функцію відгуку (параметр оптимізації). Тому, на першому етапі дослідження завжди перевіряється можливість описати досліджуваний процес за допомогою лінійної моделі, яка може бути використана для передбачення значення досліджуваної функції в різних точках обраного факторного простору (інтерполяційна модель) або для пошуку області оптимуму “методом крутого сходження”. Для знаходження лінійної моделі застосовуються плани 1-го порядку. В кожному досліді окремий фактор може приймати тільки одне із декількох значень, які називаються рівнями. Найбільш розповсюдженим планом цієї групи є повний факторний експеримент (ПФЕ), в якому кожний рівень одного фактора комбінується зі всіма рівнями решти факторів. Для отримання лінійної моделі кількість рівнів варіювання r всіх факторів приймається сталим та мінімально можливим (r=2). Такі плани називаються ПФЕ типу 2 k, де k – кількість досліджуваних факторів. Так як мають місце неконтрольовані випадкові збурення, то зміна При дослідженні технологічних процесів виготовлення або ремонту деталей в якості вихідних параметрів приймають: продуктивність, точність, якісні характеристики. Під оптимізацією потрібно розуміти найкраще розв’язання поставленої задачі, яке зводиться до знаходження екстремуму, тобто мінімуму або максимуму однієї або декількох змінних величин. Оптимальний варіант обирають за допомогою цільової функції (критерію оптимізації), під якою розуміють функцію, екстремум значення якої потрібно встановити. Реалізація методу математичного планування експерименту передбачає чітке розділення факторів на залежні та незалежні, на керовані та некеровані. За попередньо проведеними експериментами та дослідженнями знаходять допустимі межі зміни режимів х 1, х 2, х 3, х 4, а саме верхній (+) та нижній (–) рівні процесу. На основі даних дослідів складають матрицю багатофакторного експерименту та рівняння регресії, загальний вид якого наступний:
Вільний член рівняння ао та коефіцієнти аі відповідно знаходяться за формулами:
де n – кількість дослідів; Yiекс – експериментальне значення цільової функції. При складанні матриці планування (таблиця 10.1) ПФЕ переходять до кодованих значень кожного фактора, що дозволяє здійснити лінійне перетворення координат факторного простору з переносом початку координат в центр досліджуваної області та вибором масштабів за новими осями в одиницях інтервалів варіювання факторів, тобто план набуває стандартної форми. Для цього використовується залежність:
де хk – кодоване значення k – го фактора; хі – поточне значення і – го фактора; хо – основний рівень зміни фактора; ∆х – інтервал варіювання фактора.
Основні рівні та інтервали варіювання для факторів можуть бути вибрані на основі апріорних даних, на основі аналізу літературних джерел або на основі результатів раніше проведених експериментів. Після обробки даних багатофакторних експериментів можуть бути отримані математичні моделі процесу в простій матричній формі, які відображають зв’язки досліджуваних факторів з вихідними параметрами. Таблиця 10.1 – Матриця планування експерименту для
Незалежно від кількості факторів для отримання оптимальної математичної моделі необхідно, щоб матриця ПФЕ мала наступі властивості: 1. Симетричність відносно центра експерименту: алгебраїчна сума елементів вектор-стовпця кожного фактора дорівнює нулю, тобто:
де j – номер фактора j =1, 2, …, k; i – номер досліду; N – кількість дослідів. 2. Умова нормування даних: сума квадратів елементів кожного стовпця дорівнює кількості дослідів, тобто:
Це свідоцтво того, що значення факторів в матриці задаються +1 та –1. 3. Ортогональність матриці планування: сума по членних добутків любих двох вектор-стовпців дорівнює нулю, тобто:
де j ≠ u, j,u = 0, 1, 2, …, k.
Як відомо, будь – яку довільну функцію, якщо вона не має нескінчених розривів, можна розкласти в ступеневий ряд Тейлора. Тому в теорії експерименту частіш усього математичний опис представляється у вигляді поліному шляхом розкладу в ряд Тейлора:
де bо, bj, bij, bjj – сталі коефіцієнти рівняння, оцінки яких потрібно визначити в результаті постановки та проведення пасивного експерименту; n – кількість найбільш суттєвих вхідних величин, які отримані в результаті відсіюючого експерименту. Так як для обробки даних з метою відшукування оцінок коефіцієнтів рівняння (6.10) та для статичної оцінки результатів пасивного експерименту застосовуються методи регресивного аналізу, то повинен бути виконаний ряд передумов: 1. Результати спостережень у 1, у 2, …, уn вихідної величини в точках факторного простору є незалежні випадкові величини, які розподілені за нормальним законом, а процес зміни 2. Дисперсії 3. Всі значення вхідних величин xj( 4. Вхідні величини xj( 5. Всі сусідні вимірювання по кожній j -тій вхідній величині повинні бути незалежними. Кількість коефіцієнтів рівняння визначають об’єм експерименту. Тому вибирають такий поліном, який містить якомога менше коефіцієнтів, але задовольняє вимозі простоти та адекватності, під якою розуміється здатність моделі прогнозувати результати експерименту в деякій області з потрібною точністю. В загальному випадку, для будь-якої кількості факторів коефіцієнти рівняння регресії обчислюються за формулою:
де j = 0, 1, 2, 3,..., k – номер фактора (нуль записаний для обчислення b0). Якщо матриця планування є симетричною, то
і т.д. Обчислення коефіцієнтів при ефектах взаємодії двох факторів здійснюється за формулою:
де u, j = 1, 2, 3,..., k – номери факторів, u ≠ j.
Послідовність планування досліду Існують попередній та основний етапи: Попередній включає в себе вивчення та аналіз всіх даних. Дослідник повинен: 1. Скласти повний перелік факторів (краще в дослід включати більше, ніж щось виключати). 2. Задатися приблизними межами зміни факторів. 3. Потрібно вибрати параметр оптимізації у відповідності з поставленою задачею. 4. Вибрати математичну модель, яка включає цільову функцію та обмеження. Основний етап включає: 1. Планування досліду. 2. Проведення досліду. 3. Проводять обробку результатів досліду. 4. Інтерпретація результатів досліду. Основна схема проведення розрахунків: 1. Здійснюється перетворення факторів. 2. Відсіювання грубих похибок експерименту. Для відсіву беруться крайні значення. 3. Після того, як провели відсіювання, роблять перевірку на відтворення дослідів за критерієм Кохрена. Знаходимо відношення максимальної дисперсії до суми дисперсій в якомусь досліді. Це відношення – розрахункове значення Кохрена. Дисперсія відтворювання розраховується не тільки по рядкам плану, а й по експерименту в нульовій точці. 4. Після розрахунку коефіцієнта Кохрена, переходимо до розрахунку коефіцієнта рівняння регресії. 5. Перевіряємо гіпотезу про статистичну значимість коефіцієнта рівняння регресії за допомогою коефіцієнта Стьюдента. Критерій Стьюдента використовують для розрахунку довірчого інтервалу. 6. Перевірка адекватності математичної моделі здійснюється за допомогою критерію Фішера. Критерій Фішера визначається, як відношення дисперсії неадекватності до дисперсії відтворювання. Адекватність математичної моделі перевіряють за коефіцієнтом множинної кореляції. Чим ближче коефіцієнт множинної кореляції до одиниці, тим більш точно математична модель описує процес, що вивчається. Використовується у випадку, коли математична модель не забезпечує потрібної точності, інші коефіцієнти – непрямі критерії адекватності математичної моделі. Інтерпретація математичної моделі може здійснюватись графічним або аналітичним способами. Графічний спосіб Робляться розрізи поверхні відгуку, отримуємо ізолінії, які можна відобразити на площині. Один із факторів змінюється, а інші залишаються незмінними. Аналітичний спосіб Інтерпретувати аналітичним методом можна в факторах, що кодуються. 1) Величина коефіцієнта моделі – кількісна міра цього впливу при умові, що інтервали варіювання факторів порівнювальні (їх величина знаходиться в межах 10...25% від максимальної величини значення факторів). Про характер впливу факторів судять за знаком коефіцієнтів. При багатофакторному плануванні розглядають ефекти взаємодії. При додатних значеннях коефіцієнтів при ефекті взаємодії можна говорити, що для збільшення параметра оптимізації потрібне одночасне збільшення або зменшення факторів. Для зменшення параметра оптимізації необхідно фактори змінювати в різних напрямках. Якщо значення коефіцієнта від'ємне, то для збільшення параметра оптимізації фактори повинні змінюватись в різних напрямках. Для зменшення параметра оптимізації потрібне одночасне зменшення або збільшення факторів. 2) Ранжирування факторів. Якщо якийсь фактор має малий коефіцієнт (не входить в довірчий інтервал), то фактор незначний. Сигнал про не значимість факторів повинен бути перевіреним. 3) Розбіжність апріорних відомостей з результатами може відбуватися по двом причинам: Ø невірна уява про досліджуємий процес; Ø в експерименті є помилки. Для виключення впливу систематичних факторів необхідно проводити рандомізацію.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 . (10.1)
. (10.1) носить випадковий характер, а тому для отримання математичного описання в цьому випадку застосовуються методи регресивного аналізу на основі статистичних даних, які накопичені в результаті постановки експерименту.
носить випадковий характер, а тому для отримання математичного описання в цьому випадку застосовуються методи регресивного аналізу на основі статистичних даних, які накопичені в результаті постановки експерименту.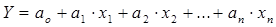 . (10.2)
. (10.2)
 , (10.3)
, (10.3) , (10.4)
, (10.4) , (10.5)
, (10.5) . (10.6)
. (10.6)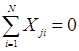 , (10.7)
, (10.7)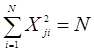 . (10.8)
. (10.8) , (10.9)
, (10.9) (10.10)
(10.10) повинен бути стаціонарним в часі.
повинен бути стаціонарним в часі. цих випадкових величин повинні бути рівні одна до одної (вибіркові оцінки S2l однорідні).
цих випадкових величин повинні бути рівні одна до одної (вибіркові оцінки S2l однорідні). ) повинні вимірюватись зі зневажаючи малою помилкою в порівнянні з помилкою вимірювання вихідної величини
) повинні вимірюватись зі зневажаючи малою помилкою в порівнянні з помилкою вимірювання вихідної величини  ) не повинні бути корельовано між собою.
) не повинні бути корельовано між собою.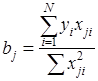 , (10.11)
, (10.11) , тоді після відповідних скорочень формули для обчислення коефіцієнтів матимуть вигляд:
, тоді після відповідних скорочень формули для обчислення коефіцієнтів матимуть вигляд: , (10.12)
, (10.12)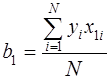 (10.13)
(10.13) , (10.14)
, (10.14)


