
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка статистичних гіпотезСодержание книги
Поиск на нашем сайте При дослідження технологічних процесів, а також при оцінці ефективності запропонованих заходів по їх удосконаленню часто виникає необхідність у перевірці однорідності продукції, що випускається, і якості функціонування самого технічного об'єкту чи технологічного процесу. Для вирішення цих задач можна скористатися статистичними методами перевірки гіпотез про приналежність досліджуваних вибірок одній генеральній сукупності по двом вибірковим середнім, та двом вибірковим дисперсіям. При проведенні технологічних досліджень порівнюють дві або більше сукупностей результатів, отриманих у рівних умовах, з метою визначення істотності розходження між ними, Необхідність такого порівняння може виникати при дослідженні випадкових величин, наприклад, при порівнянні точності деталей, що виготовляються на різних верстатах або за різними варіантами технологічних. процесів, при порівнянні періодів стійкості інструментів різних партій, шорсткості поверхні при різних методах обробки тощо. Порівняння двох вибірок випадкових величин дозволяє встановити, належать порівнювані вибірки одній генеральній сукупності або двом різним генеральним сукупностям, тобто між ними розходження є випадковим, неістотним або закономірним, що виникає в результаті якоїсь якісної зміни в умовах проведення процесу. У залежності від кількості проведених спостережень або закону розподілу, якому підкоряються випадкові величини, методи порівняння двох вибірок можуть бути різними. Розглянемо два з них, що найбільш поширені. Оцінка істотності розходження з допомогою t-критерія Стьюдента Критерій Стьюдента (t - критерій) може бути успішно застосований для порівняння вибірок лише в тому випадку, коли досліджувані випадкові Для порівняння необхідно розрахувати величину tрозр за формулою
де σ1, σ2 - середні квадратичні відхилення випадкових величин; N1, N2 - число експериментів (або вимірювань) у порівнюваних вибірках. Отримане за формулою (6.1) значення tрозр порівнюється з табличною величиною нормованого відхилення t0 Кількість ступенів волі для визначення табличного значення t0 розраховується за формулою: f = N1 + N2 - 2 (6.2) Якщо при цьому дотримується умова tрозр≤ t0, то імовірністю р можна стверджувати, що обидві вибірки належать до однієї генеральної сукупності і відмінності, що існують між ними, неістотні. Якщо tрозр>t0, то отримане значення слід вважати неістотним і відносити вибірки до однієї сукупності не можна. Оцінка істотності розходження з допомогою критерію Пірсона χ2 Критерій χ2 є непараметричним критерієм, тобто не залежить від закону розподілу. Цей критерій слід застосовувати в тих випадках, коли розподіл досліджуваних величин підкоряється закону, що відрізняється від нормального, або тоді, коли закон розподілу невідомий. Нехай є дві вибірки обсягом N1 і N2. Усі значення обох вибірок розбиваються на n однакових інтервалів і підраховують число частот у кожному інтервалі (відповідно m1 для однієї вибірки і m2 — для другої). Критерій χ2 розраховується за формулою:
За найденим значенням χ2 при кількості ступенів волі f=n-1 знаходиться величина р(х2). Звичайно вважають, що коли р(χ2) >0,5 (або 0,01), то вибірки належать до однієї генеральної сукупності. У випадку рівності обсягу порівнюваних вибірок (N1=N2=N) формула для визначення χ2 спрощується:
Порядок виконання роботи 1. Попередньо ознайомитися з теоретичними відомостями і вникнути в суть виконуваної роботи. 2. Отримати індивідуальне завдання у викладача. 3.Провести розрахунок основних параметрів розподілів. Побудувати графіки (полігон, криві розподілу). Порівняти вибірки за допомогою t-критерію Стьюдента. 4. Зробити висновки КОНТРОЛЬНІ ЗАПИТАННЯ 1. За допомогою якого критерію оцінюють істотність розрахунків 2. Що таке ступінь волі 3. В яких випадках використовують критерій Пірсона χ2 ЛІТЕРАТУРА 1. Бондаренко С.Г. Розмірні розрахунки: Навч. посібник. – Львів: Магнолія, 2007. – 500 с. 2. Пальчевський Б.О. Дослідження технологічних систем (моделювання, проектування, оптимізація): Навч. посібник. – Львів: Світ, 2001. – 232 с. 3. Рыжов Э.В., Горленко О.А. Математические методы в технологических исследованиях. - Киев: Наук, думка, 1990. – 184 с. 4. Салонин И.С. Математическая статистика в технологи машиностроения. - Г.: Машиностроение, 1972. – 215 с.
Лабораторна робота № 7
|
||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |

 величини підкоряються нормальному закону розподілу або близьким до нього наприклад, усіченому нормальному закону.
величини підкоряються нормальному закону розподілу або близьким до нього наприклад, усіченому нормальному закону.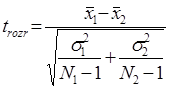 (6.1)
(6.1) ,
, 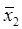 - середні значення випадкових величин у порівнюваних вибірках;
- середні значення випадкових величин у порівнюваних вибірках; (6.3)
(6.3) (6.4)
(6.4)


