
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення прискорення вільного падіння за допомогою математичного маятникаСтр 1 из 10Следующая ⇒
РОБОТА 1.1 ВИЗНАЧЕННЯ ПРИСКОРЕННЯ ВІЛЬНОГО ПАДІННЯ ЗА ДОПОМОГОЮ МАТЕМАТИЧНОГО МАЯТНИКА Мета роботи: 1) виміряти прискорення вільного падіння за періодом коливань математичного маятника; 2) вивчити методику математичної обробки результатів прямих і непрямих вимірювань; 3) вивчити закони гармонічного коливального руху. Прилади та обладнання: важка кулька, яка підвішена на легкій нитці, що не розтягується; вертикальна шкала; секундомір. Рух тіла під дією тільки однієї сили тяжіння називається вільним падінням, а прискорення, якого набуває при цьому тіло, - прискоренням вільного падіння g.
Математичним маятником називається матеріальна точка, яка підвішена на тонкій невагомій нитці, що не розтягується. Ця матеріальна точка здійснює коливання у вертикальній площині під дією сили тяжіння. На практиці математичним маятником можна вважати важке тіло, яке підвішене на легкій недеформованій нитці, довжина якої в багато разів більша за розміри тіла. На рис.1 видно, що сила F, яка повертає маятник у напрямку до положення рівноваги, при малих кутах відхилення
де Таким чином, сила F пропорційна куту відхилення маятника від положення рівноваги, отже, пропорційна зміщенню маятника від цього положення. Така сила викликає гармонічний коливальний рух. Період коливань математичного маятника Т залежить від довжини маятника l і прискорення вільного падіння:
Розв’язуючи (2) відносно g, одержимо:
звідки випливає, що визначення прискорення вільного падіння зводиться до вимірювання довжини маятника та періоду його коливань. Порядок виконання роботи 1. Установлюють певну (якомога більшу) довжину нитки маятника і знаходять значення l, вимірюючи для цього відстань від точки підвісу до центра ваги підвішеного тіла. 2. Відводячи маятник від положення рівноваги на малий кут (5-10o), визначають проміжок часу, за який здійснюється N = 50 повних коливань. Вимірювання повторюють не менше трьох разів. 3. Обробляють результати вимірювань l і t. 4. Розраховують середнє значення величини і середнє значення величини
5. Визначають відносні похибки результатів прямих і непрямих вимірювань: 6. Розраховують довірчу границю сумарних похибок і записують результат визначення прискорення вільного падіння у вигляді
1. Оформлюють звіт і результати заносять у таблицю.
Запитання та вправи для самоконтролю 1. Сформулюйте закон всесвітнього тяжіння. 2. Поясніть різницю між вагою і силою тяжіння. 3. Запишіть залежність прискорення вільного падіння від висоти над поверхнею Землі та географічної широти місцевості. 4. У чому полягає різниця між фізичним і математичним маятниками? Порівняйте вирази для їх періодів коливань. 5. Запишіть диференціальне рівняння гармонічних коливань та його розв'язок. Поясніть зміст понять "зміщення", "амплітуда", "початкова і повна фази", "період", "частота коливань". 6. Від яких величин залежить повна енергія гармонічних коливан
РОБОТА 1.2 Порядок виконання роботи 1. Записують до таблиці задані значення мас m і 4m1 і задану викладачем висоту h падіння тягаря m. 2. Штангенциркулем вимірюють діаметр шківа d у двох різних місцях при розмотаній і намотаній нитці і визначають 3. Розміщують тягарці на спицях на однаковій відстані r від осі маятника так, щоб маятник знаходився у байдужній рівновазі; визначають 4. Відмітивши початкове положення тягаря m і надавши йому можливість падати уздовж шкали, визначають t 1– час падіння тягаря з висоти h. Вимірювання проводять три рази, результати заносять до таблиці. 5. Знімають тягарці m 1 зі спиць і знову тричі визначають час падіння t 2 тягаря m з висоти h. 6. Розраховують середні значення 7. Оцінюють довірчі границі сумарних похибок (при достовірності не меншій 0,95) і відносні похибки результатів прямих вимірів та заносять їх до таблиці. 8. Знаходять середнє значення
9. Оформлюють звіт і висновки. Впевнюються в тому, що теоретичне значення моменту інерції чотирьох тягарців
Запитання та вправи для самоконтролю 1. Дайте визначення кутових швидкості та прискорення і покажіть, як вони зв’язані з відповідними лінійними величинами. 2. Дайте визначення нормального і тангенціального (дотичного) прискорень і розкрийте їх фізичний зміст. 3. Дайте визначення моментів інерції матеріальної точки та тіла довільної форми; розкрийте фізичний зміст моменту інерції. 4. Як визначається момент сили відносно точки? Відносно осі? Відповідь проілюструйте рисунком. 5. Сформулюйте і запишіть основне рівняння динаміки обертального руху. 6. Запишіть вираз для кінетичної енергії тіла, що обертається навколо нерухомої осі. 7.Як визначається момент імпульсу тіла відносно осі обертання? Сформулюйте закон збереження моменту імпульсу.
РОБОТА 1.3 КРУТИЛЬНИХ КОЛИВАНЬ
Мета роботи: І) вивчити динаміку обертального руху твердого тіла; 2) визначити момент інерції тіла методом крутильних коливань. Прилади та обладнання: крутильний маятник, циліндр, секундомір, штангенциркуль.
Період коливань маятника T зв'язаний з його моментом інерції співвідношенням:
де k – модуль кручення підвісу, який чисельно дорівнює моменту сили, що закручує дріт на кут в один радіан.
Розв'язуючи сумісно (1) і (2), одержують:
де m, d –маса і діаметр циліндра. Порядок виконання роботи 1. Записують задане значення маси циліндра m. 2. Вимірюють штангенциркулем діаметр циліндра d (не менше трьох разів). 3. Крутильний маятник приводять у коливальний рух, повернувши його на невеликий кут (20-30°). Вимірюють час t тридцяти коливань (N =30). Вимірювання повторюють п'ять разів. 4. На диск ставлять циліндр і, повторюючи вимірювання (див. п.3), визначають час t1. 5. Розраховують середнє значення < t >, < t1 >, < d >. 6. Обчислюють середнє значення періодів коливань 7. Визначають відносні похибки і довірчі границі сумарних похибок результатів вимірювань, використовуючи формули:
2. Оформлюють звіт і висновки,заносячи дані в таблицю.
Запитання та вправи для самоконтролю 1. Дайте визначення моменту інерції матеріальної точки і тіла довільної форми. 2. Запишіть і сформулюйте теорему Штейнера, проілюструйте рисунком. 3. Наведіть відомі Вам моменти інерції тіл симетричної форми. 4. Виведіть формулу кінетичної енергії тіла, що обертається. 5. Дайте визначення моменту імпульсу твердого тіла, що обертається відносно осі обертання. 6. Запишіть і сформулюйте основний закон динаміки обертального руху. РОБОТА 1.4 Порядок виконання роботи
І. Вимірюють лінійкою довжину l стержня від опори А до точки В прикладення деформуючої сили (тобто до ребра призми, на якій підвішене тягар). 2. Вимірюють штангенциркулем ширину a,товщину b стержня у вузькій прямокутній його частині. 3. У середньому положенні С закріплюють стрілочний індикатор так, щоб рухомий щуп був засунутий у корпус індикатора. При утворенні стріли прогину щуп повинен виходити з корпусу індикатора. 4. Поворотом зовнішнього кільця з насічкою на боковій поверхні встановлюють шкалу індикатора в нульове положення. 5. Чашку підвісу послідовно навантажують плоскими важками масою від 1 до 5кг, а потім розвантажують до 0кг. Для кожного навантаження 6. Будують графіки залежності F від λ при навантаженні і розвантаженні (вони практично зливаються в одну пряму лінію, що проходить через початок координат, оскільки при вказаних навантаженнях деформація згину є пружною). 7. Користуючись графіком, визначають величину 8. Розраховують середнє значення модуля Юнга за формулою (4) і відносну похибку вимірювань за формулою
9. Визначають довірчу границю 10. Оформлюють звіт і висновки, вносячи дані в таблицю.
Запитання і вправи для самоконтролю
1. Дайте визначення абсолютної і відносної, пружної і непружної та залишкової деформації. 2. Перелічіть відомі види деформації. 3. Запишіть і сформулюйте закон Гука (в загальному вигляді і для одностороннього розтягу або стиску). 4. Розкрийте фізичний зміст модуля Юнга 5. Нарисуйте діаграму розтягу і вкажіть точки, що відповідають границям пружності і міцності. Вкажіть границі виконання закону Гука і границі пластичних деформацій. 6. Поясніть відмінності в пружних властивостях пластичних і крихких, а також аморфних і кристалічних тіл.
РОБОТА 1.5 Порядок виконання роботи 1.Вимірюють за допомогою штангенциркуля діаметри d і D валика та диска в трьох різних місцях і визначають їх радіуси 2. Помітивши початкове положення маятника, пускають його падати вздовж шкали і в момент пуску включають секундомір. Визначають час повного розкручування. Вимірювання t виконують тричі для одного і того ж самого значення S. Результати вимірювань заносять до таблиці. 3. За середніми значеннями < S >, < t >, < R > і < r > визначають експериментальне aе та теоретичне aT значення прискорення центра мас за формулами (8) і (7). Результати обчислень заносять до таблиці. 4. Оцінюють довірчі границі сумарних похибок і відносні похибки результатів прямих вимірювань. 5. Визначають довірчі границі сумарних похибок непрямих вимірювань за формулами
6. Порівнюють значення aе і aT з урахуванням довірчих границь їх сумарних похибок. Аналізують можливі причини розбіжності результатів.
Запитання і вправи для самоконтролю 1. Дайте визначення кутової швидкості та кутового прискорення. 2. Як зв'язані лінійна та кутова швидкості, лінійне та кутове прискорення? 3. Що таке момент сили? 4. Що таке момент інерції, в яких одиницях він вимірюється? Наведіть приклади моментів інерції тіл симетричної форми. 5. Запишіть і сформулюйте основний закон динаміки обертального руху. 6. Дайте визначення моменту імпульсу, запишіть і сформулюйте закон збереження моменту імпульсу і наведіть приклади, що ілюструють цей закон.
РОБОТА 1.6 Порядок виконання роботи 1. Відхиляють маятник від положення рівноваги на малий кут (5-8°) і, пропустивши 1-2 коливання, визначають за допомогою секундоміра час t 1 п'ятдесяти повних коливань. Вимірювання величини t 1 повторюють тричі. 2.Перевертають маятник і тричі вимірюють час t 2 п'ятдесяти повних його коливань у новому положенні. 3.Результати всіх шести вимірювань часу t обробляють за стандартною формою. 4.Розраховують середнє значення періоду < Т > за формулою 5.Розраховують відносні похибки
6.Розраховують довірчу границю сумарних похибок вимірювань величини g при достовірності Р≥ 0,95, тобто Записують довірчий інтервал у вигляді 7.Оформляють звіт і висновки, для чого заносять дані в таблицю
Запитання та вправи для самоконтролю 1.Дайте визначення гармонічних коливань на поясніть зміст понять "амплітуда", "частота", "циклічна частота", "період", "фаза". 2. Які коливання називають вільними (власними)? 3. Що таке фізичний маятник? Приведена довжина фізичного маятника. 4. Які сили називають квазіпружними? Наведіть приклади. 5.Дайте визначення моменту інерції твердого тіла і радіуса інерції. 6. Запишіть і сформулюйте теорему Штейнера та наведіть рисунок, що її ілюструє. 7. Поясніть, як і чому прискорення вільного падіння залежить від широти місцевості. РОБОТА 1.7 Порядок виконання роботи 1. Опорну призму закріплюють на самому кінці стержня-маятника. Ребром опорної призми маятник ставлять на підставку; відхиливши його від положення рівноваги на малий кут ( 2. Повторюють вимірювання (див. п.1) через кожні 4см і дані заносять у таблицю. Треба одержати 10-12 значень періоду (періоди можуть відрізнятися на соті долі секунди, їх необхідно визначити дуже ретельно). 3. За даними таблиці будують графік функції T=T (d) (див. рис.2 на стор.104). По осі абсцис відкладають відстань між серединою стержня і ребром опорної призми, по осі ординат - значення періоду. Через експериментальні точки, нанесені на графік, проводять плавну криву так, щоб приблизно однакова кількість точок була розташована по обидві сторони кривої. Графік необхідно будувати тільки на міліметровому папері. 4. Паралельно осі абсцис проводять пряму так, щоб вона двічі перетинала криву T=T (d). Знаходять значення ординати T та абсцис d1 і d2 точок перетину і визначають приведену довжину L = d1+d2. Прискорення вільного падіння g обчислюють за формулою (5), наведеною, мінімум для трьох значень приведеної довжини і періоду; потім знаходять середнє арифметичне.
Запитання та вправи для самоконтролю 1. Що таке фізичний маятник? За яких умов його коливання є гармонічними? 2. Що таке приведена довжина фізичного маятника? 3. Дайте визначення моменту інерції твердого тіла та радіуса інерції, виразіть радіус інерції однорідного стержня через його довжину. 4. Сформулюйте теорему Штейнера і наведіть рисунок, що. її ілюструє. 5. Розкрийте математичний та фізичний зміст поняття фази коливань. На яку величину змінюється фаза за час, що дорівнює періоду? Відповідь обґрунтуйте. 7. За яких умов виникає явище невагомості?
РОБОТА 1.8 Порядок виконання роботи 1. За допомогою установочних гвинтів встановлюють підставку маятника горизонтально. 2. За відсутності поновлюючих пружин відхиляють маятник на невеликий кут ( 3. Встановлюють те ж саме значення A0 і повторюють вимірювання (див. п.2) для n = 20, ЗО, 40, 50, 60, 70. Результати заносять у табл.1. 4. Вимірювання (див.п.п.2,3) повторюють за наявності поновлюючих пружин. Результати заносять у табл.2. 5. Обчислюють значення 6. Для маятника з пружинами і без них будують на одному і тому ж самому графіку за даними таблиці І та 2 залежності відношення амплітуд 7. Для маятника з пружинами будують графік, відкладаючи по осі абсцис кількість коливань n, а по осі ординат – значення
8. Аналогічно обчислюють логарифмічний декремент загасання δ0 для маятника без пружин. 9. За допомогою секундоміра визначають періоди Т і Т о коливань маятника з пружинами і без них, вимірюючи проміжки часу t 50 повних коливань:
Розраховують коефіцієнт загасання
Розрахунки заносять у табл.3.
1. Результати розрахунків для маятника без пружин; А0=…
2. Результати розрахунків для маятника з пружинами; А0=…
3.
Запитання та вправи для самоконтролю 1. Складіть диференціальне рівняння власних незагасаючих коливань і залишіть його розв'язок. 2. Складіть диференціальне рівняння власних коливань з урахуванням сил тертя; запишіть його розв'язок і зробіть аналіз. 3. Як залежить амплітуда загасаючих коливань від часу? Запишіть вираз і проілюструйте графіком. 4. Що таке коефіцієнт загасання? Який його фізичний зміст? 5. Дайте визначення логарифмічного декременту загасання; покажіть, як він зв'язаний з коефіцієнтом загасання і розкрийте його фізичний зміст. РОБОТА 2.1 Порядок виконання роботи 1. Вимірюють відстань l між мітками " a " і " b " циліндричної посудини, що наповнена рідиною (гліцерин, рицинова олія). 2. Мікрометром вимірюють діаметр d трьох кульок (приблизно однакових). 3. Кидають кульку в рідину так, щоб вона рухалася вздовж центральної частини циліндра; вимірюють час падіння t між мітками " a " і " b ". 4. Експериментальні дані d, l, t і табличні 5. Розраховують значення 6. Визначають відносні похибки і довірчі границі для одного з вимірювань за формулами:
Питання та вправи для самоконтролю 1. Поясніть механізм виникнення сил внутрішнього тертя. 2. Сформулюйте і запишіть закон внутрішнього тертя (закон Ньютона), дайте ілюструючий рисунок. 3. Що називається градієнтом швидкості? Який йoгo зміст? 4. Що називається коефіцієнтом внутрішнього тертя? В яких одиницях він вимірюється? Який його фізичний зміст? 5. За яких умов кулька рухається в рідині рівномірно? 6. Сформулюйте і запишіть закон Стокса.
РОБОТА 2.2 ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ПУАССОНА ГАЗУ МЕТОДОМ АДІАБАТИЧНОГО РОЗШИРЕННЯ (МЕТОД КЛЕМАНА-ДЕЗОРМА)
Мета роботи: визначити коефіцієнт Пуассона повітря і порівняти результат експерименту з висновками молекулярно-кінетичної теорії газів. Прилади та обладнання: закритий скляний балон з краном, манометр, насос. Молярною теплоємністю С будь-якої речовини називають фізичну величину, що чисельно дорівнює кількості теплоти, яку треба надати одному молю цієї речовини для підвищення його температури на один кельвін. Теплоємність газу суттєво залежить від умов, за яких надають теплоту. Так, якщо нагрівається газ при сталому об'ємі, то кількість теплоти витрачається на збільшення його внутрішньої енергії. Якщо ж газ нагрівати при сталому тиску, то він потребує ще додаткової кількості теплоти для виконання роботи при розширенні. Тому молярна теплоємність CP при сталому тиску більше молярної теплоємності при сталому об'ємі CV. Зв'язок між ними показує співвідношення Майєра:
де R – універсальна газова стала. Безпосередні виміри CP і CV здійснити важко, оскільки теплоємність газу є малою часткою теплоємності посудини, що містить газ. Легше виміряти відношення величин
де i – число ступенів свободи молекули. Коефіцієнт Пуассона γ входить до рівняння Пуассона:
яке описує зв'язок між тиском P і об'ємом V ідеального газу при адіабатичному процесі.
Метод Клемана-Дезорма для визначення відношення теплоємностей газів У скляний балон A (рис.1) за допомогою насоса накачують повітря. При швидкому накачуванні температура останнього дещо підвищується, а тому потрібно зачекати 2-3 хв для встановлення в балоні тієї ж самої температурі, що і в навколишньому середовищі. Цей стан газу будемо вважати початковим і характеризувати параметрами V 1, T 1, P 1. На рис.2 даний стан зображено точкою 1. При цьому
де Pатм – атмосферний тиск, h 1 – надлишок тиску над атмосферним. Далі відкривають кран К балона на дуже короткий проміжок часу і перекривають його у той момент, коли тиск всередині балона дорівнюватиме атмосферному. При цьому газ перейде в новий стан з параметрами V 2, T 2, Pатм (на рис.2 даний стан зображено точкою 2). Оскільки розширення повітря відбувається швидко, то можна вважати, що процес переходу газу із стану 1 у стан 2 адіабатичний. Тому для нього можна застосувати рівняння Пуассона.
Підкреслимо, що T 2< T 1 оскільки при адіабатичному розширенні газ охолоджується. Через 2-3 хв. газ нагріється до температури навколишнього повітря Т 1. При нагріванні об'єм V 2 залишається без змін, а тиск підвищується до значення
де h 2 – надлишок тиску над атмосферним після адіабатичного розширення та ізохоричного нагрівання до температури T 1. Параметри нового стану 3 позначимо через V 2, Р 2, Т 1, (на рис.2–точка 3). Істотно, що в станах 1 і 3 газ має однакову температуру, отже, стани 1 і 3 знаходяться на одній ізотермі. Тому до них можна застосувати закон Бойля - Маріотта:
Після ряду перетворень з рівнянь (1) і (2) отримаємо:
Порядок виконання роботи 1. Накачують у балон A повітря, не виходячи за поділки шкали манометра. 2. Зачекавши 2-3 хв, доки температура в балоні не стане дорівнювати температурі навколишнього повітря, відраховують покази манометра h 1. 3. Відкривши на короткий час кран К, вирівнюють тиск всередині балона з атмосферним. Коли стовпчики рідини в манометрі зрівняються, кран закривають. 4. Чекають 2-3 хв., відраховують покази манометра h 2. 5. Для кожного досліду розраховують γ за формулою (3). Повторюють дослід не менше 5 разів. 6. Результати вимірювань заносять у таблицю. 7. Визначають відносну похибку результатів вимірювань:
де 8. Розраховують довірчу границю похибок результатів вимірювань:
9. Порівнюють одержаний результат з теоретичним значенням γ повітря.
Питання і вправи для самоконтролю 1. Запишіть і сформулюйте основне рівняння молекулярно-кінетичної теорії газів. 2. Дайте визначення числа ступенів свобода тіла (системи, молекули) і виразіть молярні теплоємності ідеального газу через кількість ступенів свободи молекули. 3. Дайте визначення і отримайте вираз для внутрішньої енергії ідеального газу. 4. Запишіть і сформулюйте перший закон термодинаміки, застосуйте його до різних ізопроцесів у газах. 5. Запишіть співвідношення Майєра і поясніть фізичний зміст універсальної газової сталої. 6. Який процес називається адіабатичним? Як і чому змінюється температура газу при адіабатичній зміні його об'єму? 7. Запишіть рівняння Пуассона і поясніть зміст коефіцієнта Пуассона. Зобразіть графік адіабати.
РОБОТА 2.3 Порядок виконання роботи 1. Наповнюють бюретку дистильованою водою. 2. Обережно відкривають кран, щоб краплі капали рівномірно. Відраховують n 1 – кількість крапель з об’єму 2 мл. Дослід повторюють декілька разів. 3. Те ж саме роблять з іншою рідиною. Відраховують n 2–кількість крапель з такого ж самого об'єму (2 мл). 4. За таблицями знаходять 5. За робочою формулою (8), використовуючи середні значення 6. Визначають відносну похибку
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.3.178 (0.209 с.) |
 У даній роботі прискорення вільного падіння визначається за допомогою математичного маятника.
У даній роботі прискорення вільного падіння визначається за допомогою математичного маятника. дорівнює
дорівнює , (1)
, (1) (в радіанах).
(в радіанах). . (2)
. (2) , (3)
, (3) за формулою
за формулою 
 за формулою (3).
за формулою (3). ;
;  .
.



 .
. . Перш, ніж почати експеримент, перевіряють, чи добре збалансовано маятник.
. Перш, ніж почати експеримент, перевіряють, чи добре збалансовано маятник. і
і  .
. , користуючись формулою (7), і оцінюють відносну похибку непрямого виміру за формулою
, користуючись формулою (7), і оцінюють відносну похибку непрямого виміру за формулою  і довірчу границю
і довірчу границю  за формулою
за формулою 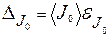 .
.  .
. , попадає в довірчій інтервал цієї величини:
, попадає в довірчій інтервал цієї величини:  .
.
 У даній роботі для визначення моменту інерції тіла неправильної форми використовують крутильний маятник, який являє собою підвішений на пружному дроті диск зі скобою (рис.1).
У даній роботі для визначення моменту інерції тіла неправильної форми використовують крутильний маятник, який являє собою підвішений на пружному дроті диск зі скобою (рис.1). , (1)
, (1) Для виключення k з виразу (1) діють так. На диску розміщують циліндр з відомим моментом інерції J ц У цьому випадку згідно з (1) період маятника дорівнюватиме:
Для виключення k з виразу (1) діють так. На диску розміщують циліндр з відомим моментом інерції J ц У цьому випадку згідно з (1) період маятника дорівнюватиме: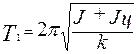 . (2)
. (2)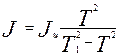 ; (3)
; (3) (4)
(4) і
і 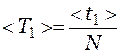 , а також середні значення моментів інерції < Jц > і < J > за формулами (4) і (З).
, а також середні значення моментів інерції < Jц > і < J > за формулами (4) і (З). ;
;  ;
;  ;
; 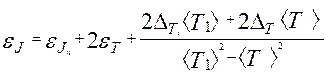
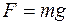 за шкалою індикатора визначають два положення стріли прогину
за шкалою індикатора визначають два положення стріли прогину  (при навантаженні і розвантаженні).
(при навантаженні і розвантаженні). як відношення ординати правого кінця графіка до відповідної абсциси (таке відношення називають кутовим коефіцієнтом).
як відношення ординати правого кінця графіка до відповідної абсциси (таке відношення називають кутовим коефіцієнтом). .
. сумарних похибок при Р ≥ 0,95.
сумарних похибок при Р ≥ 0,95. ,
, 
 та
та 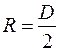 . Результати вимірювань заносять до таблиці.
. Результати вимірювань заносять до таблиці. ;
; 
 ;
; 
 і середнє значення величини < g >, використовуючи формулу (5) на с.74.
і середнє значення величини < g >, використовуючи формулу (5) на с.74. та
та  .
. .
.

 40), вимірюють за допомогою секундоміра час 50 повних коливань і обчислюють їх період.
40), вимірюють за допомогою секундоміра час 50 повних коливань і обчислюють їх період. A(nT)).
A(nT)). та
та  і заносять їх у відповідні таблиці.
і заносять їх у відповідні таблиці.
 .
. ;
;  .
. ,
,  маятника з пружинами і без них та відповідний час релаксації
маятника з пружинами і без них та відповідний час релаксації ,
,  .
.

 і
і  заносять у таблицю.
заносять у таблицю. за формулою (5) для кожного вимірювання, а потім знаходять (η).
за формулою (5) для кожного вимірювання, а потім знаходять (η). ;
; ;
;  .
.
 ,
, , яке називають коефіцієнтом Пуассона. Виходячи з уявлень класичної молекулярно-кінетичної теорії, можна показати, що для ідеального газу
, яке називають коефіцієнтом Пуассона. Виходячи з уявлень класичної молекулярно-кінетичної теорії, можна показати, що для ідеального газу ,
,

 базується на використанні методу адіабатичного розширення. Адіабатичним називається процес, який відбувається без теплообміну системи з навколишнім середовищем. Адіабатичний процес можна здійснити або за допомогою теплової ізоляції системи, або за умову короткочасності процесу (за малий проміжок часу не встигає відбутися тепловий обмін з навколишнім середовищем).
базується на використанні методу адіабатичного розширення. Адіабатичним називається процес, який відбувається без теплообміну системи з навколишнім середовищем. Адіабатичний процес можна здійснити або за допомогою теплової ізоляції системи, або за умову короткочасності процесу (за малий проміжок часу не встигає відбутися тепловий обмін з навколишнім середовищем). ,
, ;
;  . (1)
. (1) ,
, ;
;  . (2)
. (2) .
. ,
,  ,
, , c - ціна поділки шкали манометра.
, c - ціна поділки шкали манометра. .
. .
. ,
,  розраховують
розраховують  .Дані заносять.у таблицю.
.Дані заносять.у таблицю. і довірчу границю сумарних похибок
і довірчу границю сумарних похибок  за формулами
за формулами ,
,  .
.


