
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математичне моделювання хіміко-технологічних процесiвСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ХІМІКО-ТЕХНОЛОГІЧНИХ ПРОЦЕСIВ Загальні поняття
Моделювання - це вивчення об’єкту шляхом побудови і дослідження його моделі, здійснюване з певною метою і складається у заміні експерименту з оригіналом експерименту на моделі. Модель повинна будуватися так, щоб вона найбільш повно відтворювала ті якості oб’єкта, які необхідно вивчити у відповідності з поставленою метою. В усіх відносинах модель повинна бути площе об'єкту та зручне для його вивчення. Таким чином, для одного й отого ж об’єкту можуть існувати різноманітні моделі (клас моделей),відповідні різноманітним цілям його вивчення. Необхідною умовою моделювання є подобiє об’єкту та його моделі. Від спеціаліста, що займається побудовою моделей, вимагаються слідуючи основні якості: – чітке уявлення про cутність фізико-хімічних явищ, протікаючих в об’єкті; – уміння математично описувати протікаючи процеси та застосовувати засоби моделювання; – бути у стані забезпечити одержання на моделі змістовних результатів.
Цілі і завдання моделювання: 1. Оптимальне проектування нових та інтенсифікація діючих технологічних процесів. 2. Контроль за ходом процесу, одержання необхідної інформації про нього та обробка одержаної інформації з метою управління ходом технологічного процесу. 3. Рішення задач дослідження об'єктів, де ніяк не можна проводити активні експерименти (режими роботи реакторів, траєкторії космічних об’єктів і т. д.). 4. Максимальне прискорення переносу результатів лабораторних досліджень в промислові масштаби. Вимоги до моделі: 1. Витрати на утворення моделі повинні бути значно менш витрат на утворення оригіналу. 2. Повинні бути чітко визначені правила iнтерпретації результатів обчислювального експерименту. 3. Основна вимога - модель повинна бути істотної. Ця вимога укладається в тому, що модель повинна відбивати необхідні, істотні для рішення конкретного завдання властивості об'єкту. Для одного й отого ж об'єкту cкладно створити узагальнену модель, що відбиває всі його властивості. Тому важливо забезпечити істотність моделі. Класифікація моделей.
Класифікацію моделей можна проводити по різним типам ознак: - по способу пізнання: науково-технічні, художні, життєві. - по природі моделей: предметні (фізичні / матеріальні); знакові (уявні).
Рис. 1.1 Математична модель - сукупність математичних залежностей, суттєвість, що відбивається у явній формі технологічного процесу, т.є., всі істотні параметри технологічного об’єкту пов'язані системою математичних порівнянь. По повноті відбивання внутрішніх властивостей об'єкту моделювання моделі поділяють на динамічні та статичні. Динамічні моделі в основному використовуються при розробці систем автоматизованого управління процесами, бо вони враховують перехідні характеристики об'єкту. Статичнімоделі описують стаціонарні (що установилися) процеси. По використовуваному математичному апарату математичні моделі поділяються на: 1. детерміновані - при зміні будь-якого параметра значення вихідних величин визначаються однозначно. 2. статистичні - результат визначається з визначеною мірою вірогідності (т. є. неоднозначно визначається заданими параметрами). Фізичне моделювання Фізичне моделювання - це засіб дослідження на моделях, що мають однакову фізичну природу з об'єктом моделювання, тобто. становлять деякий макет об'єкту, що вивчається. Фізичні моделі відтворюють увесь комплекс властивостей явищ об'єкту. В фізичному моделюваннi важливу роль грає теорія подобiя. Її основне положення: необхідне фізичне подобiє моделі та об'єкту забезпечується лише при рівності всіх однотипних комплексів,що визначаються безрозмірних комплексів (критеріїв подобiя) у східних точках моделі та об'єкту. При фізичному моделюваннi в додаток до геометричного подобія передбачається подобiє швидкостей, сил, матеріальних середовищ і т.п. При моделюваннi на основі засобу подобiя безрозмірни комплекси грають двояку роль. По-перше, на їх основі визначають, коли модель подобна оригіналу, при цьому комплекси служать власно критеріями подобiя. По-друге, значення отих же комплексів у подібних точках і є ота кількісна міра, що і переноситься з моделі на об'єкт. Розглянемо деякі часто використовувані критерії подобiя: - Критерій Рейнольдса (критерій гідродинамічного подобiя): Re = W L/ V де W - швидкість потоку, L - розмір, що визначається, V - кiнематична в’язкість середи.
- Критерій Нуссельта (критерій теплового подобiя): Nu = a L / l де a - коефіціент теплоотдачi, l - коефіціент теплопровідностi, L - розмір, що визначається.
Критерії подобiя дозволяють установити аналогію між різними явищами. Можливість фізичного моделювання визначається наступною залежністю: f = A – R. де f - число мір волі, A - кількість параметрів, критеріїв, що характеризують процес, R - число критеріїв подобiя, які необхідно підтримувати рівними у процесі дослідження. Якщо число мір волі f < 0 - оте застосовувати фізичне моделювання не можна, бо немає волі вибору параметрів моделі. Достоїнства засобу фізичного моделювання: - наочність – фізична модель відтворює практично всі сторони оригіналу; - можливо вивчення процесу без складання його математичного опису; - можливість відтворення виробничого процесу у лабораторних умовах. Недоліки засобу фізичного моделювання: - відсутність унiверсальностi – для кожного нового процесу необхідно створювати нову модель; - висока вартість моделей для дослідження складних процесів; - неможливість застосування цього засобу для моделювання більшої частини хімічних процесів та реакторів, а також інших складних об'єктів.
Більш докладно зупинимося на останній нестачі. Застосування теорії подобiя дозволяє сформулювати вимоги до моделі, задоволення яких забезпечує можливість кількісного розповсюдження результатів експерименту з моделі на оригінал. Але в отих випадках, коли процес у оригіналі складний, задовольнити цим вимогам виявляється дуже тяжко. Коли число критеріїв, що визначають подобiє, достатньо велика, побудова подібної моделі стає нереальною задачею. Саме цим визначаються труднощі, виниклі при спробах застосування засобу подобiя для моделювання хімічних процесів та реакторів. Рядом дослідників були сформульовані критерії подобiя для наданого класу процесів. Але опинилося, що в переважній більшості випадків ці процеси настільки важки, що для дотримання подобiя моделі та оригіналу вимоглося би iдентичність дуже великого числа критеріїв подобiя зразу, забезпечити яку практично неможна. У вигляді прикладу розглянемо систему, у якій тече хімічна реакція. Виходячи з теорії подобiя, для такої системи можна скласти критерії подобiя, зокрема критерій Рейнольдса Re= W L/ V, що характеризує гідродинамічний режим, критерій Дамкеллера Da = r L / (W C), що характеризують хімічне перетворення та ін. В наданих критеріях C – концентрація вихідної речовини, що реагує, r – швидкість хімічної реакції. Інші позначення приведені вище. Критерії Re, Da (інші критерії в цілях спрощення не розглядуються) характеризують систему, що вивчається. Однак ці критерії несумісні між собою, оскільки при Re = const величина W протилежно пропорційна, а при Da = const – прямо пропорційна величині L. З приведеного зіставлення слідує, що для збереження гідродинамічного подобія швидкість струму W повинна змінюватися назад пропорційно, а для збереження хімічного подобiя - прямо пропорційно лінійному розміру L. Природно, що в одному й отому ж процесі це ніяк. Причина цього лежить не в невдалому виборі критеріїв подобiя, а у неможливості, у загальному випадку, зберегти однаковим вплив фізичних факторів на швидкість хімічного перетворення у реакторах різноманітного масштабу. В дійсності, у складних системах зміна масштабу викликає, як правило, зміну структури системи та характеру вдачі протікаючих у неї процесів. Всім відоме існування критичних розмірів системи, що містить U-235 та U-238. Ці розміри визначають співвідношенням між числом що створюються при діленні нейтронів та числом поглинаємих та відходящих назовні. З збільшенням масштабу частка часток, що губляться зменшується та змінює характер протікання процесу - замість повільного ділення наступає вибух. В хімічному реактор швидкість власне хімічного перетворення не залежить від розмірів реакційної системи. Але протікання хімічної реакції приводить до зміни складу та температури. Наслідком цього є виникнення процесів переносу речовини та тепла, бистрота яких надто істотно залежить від розмірів системи. Склад та температура у свою чергу дуже сильно впливають на бистроту хімічної реакції. Внаслідок виникає дуже складна залежність умов протікання хімічного процесу від розмірів апарату. Причому зміна розміру реактора може значно змінити як загальну швидкість процесу, так і співвідношення швидкостей реакцій, які приводять до різноманітних продуктів реакції, т. є. вибірність процесу. Таким чином, можна зробити висновок, що неможливість використання засобу фізичного моделювання для хімічних реакторів пояснює несумісністю умов подобiя фізичних та хімічних що складають процес. Цей висновок справедлив для більшості хімічних процесів та реакторів. Лише у випадку, якщо швидкість хімічного процесу не впливає на швидкість сумарного процесу наприклад, каталiтичнi процеси у галузі зовнішньої дифузії), критерії хімічного подобiя випадають та застосування теорії подобiя стає можливим. Крім отого, широко використовується фізичне моделювання гідродинамічних та теплових процесів, протікаючих в отих частинах реактора, де хімічне перетворення відсутнє (наприклад, розподілені та змішувальні будови та ін). Математичне моделювання Це найважливіший засіб сучасного наукового дослідження, основний апарат системного аналізу. Математичне моделювання – це вивчення поводження об'єкту в отих чи інших умовах шляхом рішення порівнянь його математичної моделі. У хімічній технології математичне моделювання застосовують практично на всіх рівнях дослідження, опрацювання та впровадження. Наданий засіб базується на математичному подобiї. У математично подібних об'єктів процеси володіють різноманітною фізичною природою, але описуються iдентичними порівняннями. У вигляді прикладу розглянемо декілька різноманітних по фізичній природі явищ та їх математичного опису: 1. Закон Фур'є (перенос тепла) q =-λdt/dx де: T - температура, q - тепловий потік, Х - поточна координата, λ - коефіцієнт теплопровідності. 2. Закон Фіка (перенос речовини) j =-D*dc/dx де: D - коефіцієнт дифузії, С - концентрація. 3. Закон Ньютона (перенос кількості руху) fтр=-m*dwf /dx де: w - швидкість потоку, m - в’язкість, fтр - сила тертя. 4. Закон Ома (перенос електрики) i = – c*du/dx де i -густина струму, c - питома провідність, u - потенціал. Знак (–) при коефіцієнтах порівнянь означає, що потік спрямований з областей з більшими значеннями параметра у область, де цей параметр має менше значення. В усіх чотирьох законах спостерігає подобiє математичних описаній різноманітних фізичних явищ. Тому будь-який з перелічених процесів може служити моделлю другого. Кожний з приведених законів можна з використанням визначених перерахувальних коефіцієнтів iнтерпретировати, наприклад, на електричній моделі, що ілюструє закон Ома. Серед розгляданих прикладів електрична модель є найбільш простою й може бути застосована для деяких оригіналів з різноманітною фізичною природою, т.є. вона стає універсальної. На такій моделі відтворюється не самий фізичний процес, а його математичний опис чи аналогія між законами, що виражають явища в оригіналі та у моделі. Практика наукових досліджень підтвердила, що можливо представляти процес, що вивчається на моделі, в якої протікає інший по своїй природі процес, якщо математичний опис цих процесів ізоморфен. Гомоморфiзм - ця відповідність деяких властивостей оригіналу властивостям моделі. Iзоморфiзм - взаємний гомоморфiзм, т. є. коли всі властивості моделі відповідають властивостям оригіналу. На перших порах свого розвитку математичне моделювання називалося аналоговим. Більш отого, використання засобу аналогії привело до появи аналогових обчислювальних машин - АОм. Це електронні будови, що складаються з інтеграторів, будов, що диференціюють, суматорів та підсилювачей. На АОм моделюється фізичні явища, що аналогічні ефектам електричної природи. У порівнянні з фізичним математичне моделювання -більш універсальний засіб. Математичне моделювання: - дозволяє здійснити за допомогою однієї будови (ЕОМ) рішення цілого класу задач, що мають однаковий математичний опис; - забезпечує простоту переходу від одного завдання до іншого, дозволяє вводити перемінні параметри, обурення та різноманітні початкові умови; - дає можливість проводити моделювання по частинам ("елементарним процесам"), що особливо істотно при дослідженні складних об'єктів хімічної технології; - економічнєє засобу фізичного моделювання як по витратам, так і по вартості. Емпiричний засіб
Зовнішні зв'язки будь-якої системи можна представити у вигляді такої схеми (рис. 1. 2). Вхідні параметри поділяються на три групи Х - контрольовані, але не регулюємі параметри; U - контрольовані і регулюємі параметри (керуючі параметри); Z - неконтрольовані та нерегулюємі параметри (обурення). Рис. 1.2
Модель "чорного ящикa" - модель об'єкта, створена безвідносно внутрішніх властивостей об'єкта, без врахування фізичної сутності процесів, що протікають у ньому. Дaнa модель відобрaжaє зaлежність знaчень вихідних пaрaметрів від вхідних. Математичний опис у загальному виді становить систему порівнянь виду:
В принципі ці порівняння визначають залежність i-го виходу від всіх вхідних діянь. Але установити вид функцій F принципово ніяк - адже обурення Z нам невідомі. Проте, у більшості випадків, кожне з порівнянь можна представити у вигляді
Тут функція розтрощена на дві складові: залежність F від контролюємих параметрів та похибка ("шум ") f. Тепер задача i ставиться таким образом: установити вид функції Fi та оцінити " шум " fi. Під математичною моделлю будемо розуміти саме Yi = Fi (Ui, Xi). Це порівняння, що встановлює зв'язок між вихідними та i ії вхідними параметрами, називають порівнянням регресiї. Найбільш часто цю функцію представляють алгебраїчним многочленом. Звичайно спершу розраховують більш прості многочлени, відхилення досвідчених точок від розрахункових значень порівнюють з випадковою помилкою експерименту. Якщо обидві величини одного порядку, отой опис вважають задовільним. Якщо відхилення не можна пояснити випадковою помилкою, оте розраховують більш складний многочлен. По мірі збільшення порядку многочлена точність опису зростає, але одночасно, по-перше, збільшується необхідне число опитів для знаходження коефіцієнтів многочлена, а, по-друге, ускладнюється трактова моделі. Порівняння регресiї можна отримати одним з трьох способів: 1. Пасивний експеримент. 2. Активний експеримент. 3. Визначення реакції об'єкту на стандартне обурення.
Пасивний експеримент - виробляється збиранням та аналізом інформації про стан технологічних параметрів об'єкту без спеціальної зміни вхідних параметрів процесу. Достоїнства наданого засобу - практично повністю відсутні витрати на експеримент. Недоліки: 1. У нормальних умовах експлуатації вагання технологічного режиму невеликi і тому експериментальні точки близькi друг до друга. В цих умовах на точність опису можуть сильно повіяти випадкові помилки. 2. Необхідно мати достатньо велику кількість експериментальних наданих. Активний експеримент - складається у цілеспрямованій зміні вхідних параметрів технологічного процесу. В основі цього засобу лежить планування експерименту. Практично всі процеси хімічної технології є складними і на показники процесу виявляють вплив велике число факторів. Можливі два підходу до дослідження таких многофакторних систем. Перший заснований на отому, що дослідження об'єкту розбивається на серії, в кожної з яких досліджується зміна тільки одного параметра при фіксованих інших. Другий підхід заснований на побудові плану експерименту, що передбачає зміну всіх спливаючих факторів. Такий план повинен забезпечити максимум точності та мінімум кореляції. Такий експеримент називають многофакторним. Достоїнством першого підходу є його наочність та простота iнтерпретації результатів, що отримуються. Другий підхід значно ефективнєє - при отому ж обсязі експериментальних досліджень та отієї ж точності опитів отримується істотно велика точність результатів.
Рис. 1. 3а При цьому кожний фактор приймає лише два значення - вар'ірується на двох рівнях (верхньому та нижньому).
Матрица планування для кодированих перемінних має вид (рис. 1.3б)
Рис. 1. 3б
На практиці для скорочування запису часто замість " +1 " та " –1 " просто пишуть " + ", " – ". план, що розглядається, побудовам так, що кожний фактор вар'ірується на двох рівнях, причому у опитах перебираються всі можливі комбiнації двох рівней факторів. Такий план називають планом повного факторного експерименту на двох рівнях. Визначимо значення коефіцієнтів по наступним формулам:
Активний експеримент дозволяє за рахунок цілеспрямованої зміни вхідних параметрів отримувати необхідний обсяг інформації при істотно меншому числі опитів, чим при пасивному експерименті.
Рис. 1. 4
де t – час; Свх – концентрація вхідного компонента
Дослідження об'єкту при нанесенні стандартних обурень помітно полегшує обробку інформації,що одержується. Цим способом в основному користуються при вивченні динаміки (перехідних характеристик) об'єкту, при визначенні гідродинамічних обставин та ін. При використанні емпiричних засобів математичний опис складається наступним чином: 1. Проводяться експерименти засобом "чорного ящика ", т. є. вивчається реакція об'єкту на різноманітні обурення. 2. Здійснюється статистична обробка результатів та пошук найкращий форми апроксимації одержаних даних. 3. Будується математичний опис. Єдиним критерієм застосування одержаного математичного опису є найвелика простота порівняння при хорошої апроксимації експериментальних даних.
Приклад
Одержана квадратична залежність 2. Видно, що на iнтервалі (а в) модель добре описує процес, протікаючий в оригіналі, експериментальна залежність Y=f(X) відображається кривою 1. При виході величини значення X за межі відрізку (а в) модель (крива 2) дає чималі похибки. Емпiричнi засоби корисні і застосуються для вивчення складних систем, якщо їх структура не змінюється в часу, теорія процесу невідома і (або) коли необхідно хутко одержати модель без дослідження процесу. Теоретичний засіб Цей засіб припускає складання математичного опису на основі детального вивчення та глибокого понiмання отих фізичних та хімічних закономірностей процесів, протікаючих в ньому. Складений на основі цього засобу математичний опис дає можливість з великою точністю провіщати результати протікання процесу у заданих нами умовах. Теоретичний засіб - найбільш надійний спосіб складання математичного опису. Математичний опис об'єкту складають такі частини (рис. 1. 5) Матеріальні та енергетичні баланси складаються на основі закону збереження енергії та маси: “прихід” – “витрата” = “накопичення”. Обмеження можуть бути зумовлені технологічними, технічними або економічними причинами. Експериментально-аналітичні залежності - моделі елементарних процесів, які входять у складний процес, всілякі коефіцієнти та їх залежності від параметрів.
Рис. 1. 5 Достоїнства: можливість широкої екстраполяції розділення складного процесу на окремі що складають та дослідження процесу по частинам полегшує складання моделі процесу в цілому, можливість вивчення процесу на різних рівнях. Недоліки: трудність утворення надійної теорії складних процесів неможливість використання при невідомому механізмі процесу великої витрати часу. Вибір математичної моделі Задача вибору моделі виникає при наявності для одного й отого ж об'єкту класу моделей. Вибір моделі є одним з найважливіших етапів моделювання. В кінцевому рахунку перевага отієї чи іншої моделі визначає критерій практики, що розуміє у широкому змісті. При виборі моделі треба сходити з розумного компромiсу між важкістю моделі, повнотою характеристик,що одержують з її допомогою об'єкту та точністю цих характеристик. Так, якщо модель недостатньо точна, оте її треба доповнити, уточнити введенням нових факторів може також опинитися, що надана модель занадто важка та оті ж результати можна отримати за допомогою більш простої моделі.
Рис.2.1
Оскільки в РІЗ змішування діється миттєво по всьому реактору, то Свих=C, Твих = Т. Для спрощення також приймемо, що Qвх = Qвих = Q. Позначимо: V - обсяг реактору; S - поверхня теплообміну; W - швидкість хімічного перетворення. Матеріальний баланс записується на основі закону збереження кількості речовини:
Перетврюємо: Дорівнення (2.2) стає дорівненням матеріального балансу РІЗ. Енергетичний баланс записується на основі закону збереження енергії:
де C Р - теплоємність реакційної суміші; p - густота реакційної суміші; a - коефіціент теплопередачi; S - поверховість теплообміну; Cа - усереднена об'ємна теплоемність апарату. CA = CR×xR×rR + CP×xP×rP + CK×xK×rK де xR, xP, xK - частка загального обсягу,що займається внутрішніми конструкціями,реакційною середою й каталізатором,відповідно; CR, CP,Ck - теплоємністі конструкціі реактору, реакційноі середи та каталізатора, відповідно; ×rR, rP, rK - густота матеріалу реактора,реакційноі середи, та каталізатору, відповідно. Перетворюємo дорівняння (2.3)
Дорівнення (2.4) стає дорівненнєм теплового балансу РІЗ. Дорівнення кінетикі. В загальному виді швидкість реакціі визначається як функція составу та температури реакційноі суміші: w =F(C,T) (2. 5) де: C - вектор концентрацій, T - температура;
а) проста реакція: W= kf(C); де: k - константа швидкісті реакціі,що визначається по дорівненню Аррейніуса: k = k0 * e –E/RT де: k0- предекспонента; E -eнергія актіваціі;
в) оборотна реакція: _ _ W=k1 f1 (C)-k2 f2 (C) де: k1- константа швидкісті прямої реакції, k2 - константа швидкісті зворотної реакції. Початкові умови. Початкові умови визначають поля температур та концентрацій в початковий момент часу, що, взагалі кажучи,може бути обрано довільно. t = 0; C = C поч ; T = Tпоч ; (2. 6) Обмеження. Визначають діапазон параметрів,в яких працює реактор.
Tmin < T < Tmax (Tmin і Tmax - робочий діапозон температур) Cвх min < Cвх < Cвх max (Cвх min і Cвх max - робочий діапозон вхідних концентрацій) Qmin< T < Qmax (Qmіn і Qmax- робочий діапозон oб'ємноі витрати) Дослідження моделі РІЗ Поводження об'єкту визначається сукупністю значень параметрів, які входять у математичний опис. Проведемо класифікацію параметрів моделі РІЗ. Вхідні параметри: – технологічні: Tвх, Cвх, Qвх, Tх*; – конструктивні: V, S*; – фізичні: a, CP, r, CA; – параметри, які характеризують реакцію: (–DH), E, B.
Вихідні параметри: – технологічні: Tвих, C*; – час: t. Для знаходження всього трьох вихідних параметрів необхідно задати 13 вхідних параметрів. Для спрощення дослідження моделі і скорочування кількості параметрів застосовують запис рівнянь моделі в безрозмірної формі. Вводиться ряд безрозмірних параметрів (таблиця 2.1). Таблиця 2.1
Внаслідок одержуємо модель РІЗ в безрозмІрному виді: - Матеріальний баланс:
- Єнергетичний баланс:
- Рівняння кiнетикi:
де
b= R×T0 / E - критерій Аррейнiуса; X - міра перетворення; T0 - опорна температура, К;
R - газова постійна; t - час перебування (контакту); С0 – концентрація на вході; t - віношення поточного значення часу до часу контакту (" безрозмірний час ").
Підрахуємо кількість параметрів в безмірной моделі; а) вихідні параметри: - технологічні Q, X - час t `. б) вхідні параметри: - технологічні XBX, QBX, QX. в) фізичні - b, g. г) параметри,що характеризують реакцію - В безмірної моделі 8 параметрів. Таким чином число параметрів скоротилося за рахунок зникнення конструктивних параметрів. Це є важливим достоїнством безмірноі моделі РІЗ. Рис.2.3.
Розглянемо спершу стаціонарний режим 3, що відповідає режиму роботи при температурі q3. Так як швидкості виділення і отвода тепла однакові, оте поки температура q не зміниться, режим залишається стаціонарним. Припустимо, що внаслідок випадкового обурення змінюється значення x і відбувається зміщення на величину Dq. При цьому за рахунок прискорення швидкості реакції зростає швидкість виділення тепла; це зростання діється по лінії, яка відповідає кривої тепловиділення. Одночасно, за рахунок збільшення різниці температур між температурами в реакторі і теплоносія зростає швидкість відведення тепла, це зростання діється по лінії тепловідводу. В крапці 3 лінія тепловідвода минає з більш великим кутом наклона,чим лінія тепловиділення. Тому при температурі q3 + Dq швидкість відвода виявляється вищою,ніж швидкість його виділення. В цих умовах, після зняття обурення Dq реактор почне охолоджуватися. Охолодження буде тривати до отих пор, поки температура в реакторі не стане дорівняної q3. При цій температурі швидкості від вода і виділення тепла знову зрівняються і режим знов стане стаціонарним. Навпаки, якщо внаслідок обурення (q = q – Dq) реактор почне охолоджуватися, оте після зняття обурення (тому що швидкість виділення тепла при цих умовах перевищує швидкість тепловідводу) реактор знову почне нагріватися до досягнення в ньому температури, яка дорівнює q3. Таким чином, стаціонарний режим в крапці 3 вертається до вихідного стану після зняття зовнішніх обурень, можна сказати що режим стійкий. Спроможність системи (реактора) вертатися до вихідного стаціонарного стану після зняття обурень називається стійкiстью. Інакше кажучи, вихідний стаціонарний режим є стійким, якщо після усунення джерел порушення режиму будь-які малі відхилення з течією часу прагнуть до нуля. Якщо ж значення відхилень наростають в часу, оте вихідний стаціонарний режим нестійкій. При температурі q1, відповідній стаціонарному режиму 1, з погляду стійкiстi картина повністю аналогична розглянутому вище режиму в крапці 3, тому що і в цьому випадку лінія тепловідвода іде круче, чим лінія тепловиділення і вихідний стаціонарний режим стійкий. Тепер розглянемо режим в крапці 2. Тут наклон лінії тепловідвода менш, чим лінії тепловиділення. Але також, як і в крапках 1 і 3, qR = qT і якщо немає обурень, режим буде стаціонарним. Хай сталося випадкове обурення і температура q1 підвищілася на величину Dq. При температурі q = q + Dq швидкість виділення тепла стає більше, ніж швидкість тепловідвода. І тому після зняття обурення реактор буде не охолоджуватися,а нагріватися, віддаляясь від вихідного стану. Нагрів буде тривати до отих пор, поки знов швидкість тепловиділення не буде дорівняної швидкості тепловідвода, т. є. реактор досягне нового стаціонарного стану - при температурі q3. Аналогічно, при заперечливих обуреннях реактор буде самопроiзвольно охолоджуватися до отих пор,поки не досягне стійкого стаціонарного стану при температурі q. Проведений аналіз показав, що із трьох можливих в наданих умовах стаціонарних режимів тільки два:1- при низькій температурі і, відповідно, малої швидкості реакції) і 3-при високій температурі і великої швидкості реакції є стійкимi, а третій - при проміжних значеннях температури і швидкості реакції (крапка 2) - нестійкий. Умова стійкостi Умова стійкостi визначається співвідношенням тепловідвода і тепловиділення. Режими є стійкими, якщо швидкість тепловідвода перевищує швидкість тепловиділення. Враховуючи геометричний зміст похильной умову стійкістi можна сформулювати наступним образом система стійка,якщо кут наклона крiвой тепловиділення менш, чим лінії тепловідвода
2.1.6 Вплив вхідних параметрів на стаціонарні режими. Розглянемо вплив зміни основних параметрів на вході в РІЗ на стаціонарні режими. Швидкість тепловідвода є функцією наступних параметрів: qT = f(qвх ; qх; g) (2.21)
Розглянемо вплив температури входу на стаціонарні режими. При збільшенні qвх лінія тепловідводу буде зміщатися праворуч. При цьому умови існування стаціонарних режимів будуть іншими. На рис.2.4 показані лінії тепловідтводу, збудовані при різних значеннях q.
Рис 2.4
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.85.96 (0.015 с.) |


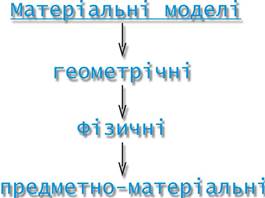
 Матеріальні моделі - зменшене (збільшене) відбивання оригіналу з збереженням фізичної суттєвості (реактор - пробiрка). Уявна модель -видображення оригіналу, що відбиває істотні риси і що виникає у свідомості людини в процесі пізнання. Образні моделі носять описовий характер. Знакові моделі — є математичними описами процесів, явищ, об’єктів і звичайно називаються математичними моделями. Знакові моделі можуть також включати у себе схеми та креслення наприклад, схема з рециклом (рис.1.1)
Матеріальні моделі - зменшене (збільшене) відбивання оригіналу з збереженням фізичної суттєвості (реактор - пробiрка). Уявна модель -видображення оригіналу, що відбиває істотні риси і що виникає у свідомості людини в процесі пізнання. Образні моделі носять описовий характер. Знакові моделі — є математичними описами процесів, явищ, об’єктів і звичайно називаються математичними моделями. Знакові моделі можуть також включати у себе схеми та креслення наприклад, схема з рециклом (рис.1.1)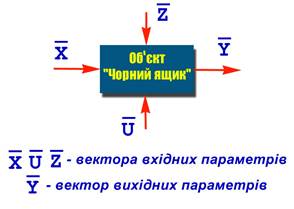 Емпiричний засіб, в основному, використовується, коли процес мало вивчений або нічого невідомо о його природі. Цей засіб також дозволяє отримати математичний опис діючого об'єкту без дослідження його внутрішньої структури.
Емпiричний засіб, в основному, використовується, коли процес мало вивчений або нічого невідомо о його природі. Цей засіб також дозволяє отримати математичний опис діючого об'єкту без дослідження його внутрішньої структури.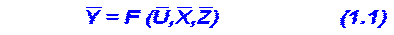
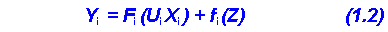
 У вигляді прикладу розглянемо вплив температури (x1), та часу перебування (x2), на вихід продукту (y2). Математичну модель отримуємо у виді полiнома 1-й міри лінійного порівняння регресії – y = b + bx + bx. Для цього використовуємо плани 1-го порядку, що будуються наступним чином. Обираємо центр області, що досліджується (центр плану), й у нього переноситься початок координат. Задаються мінімальні (min) та максимальні (max) значення вхідних параметрів х1 та х2.. Складаємо план експерименту (рис. 1.3а).
У вигляді прикладу розглянемо вплив температури (x1), та часу перебування (x2), на вихід продукту (y2). Математичну модель отримуємо у виді полiнома 1-й міри лінійного порівняння регресії – y = b + bx + bx. Для цього використовуємо плани 1-го порядку, що будуються наступним чином. Обираємо центр області, що досліджується (центр плану), й у нього переноситься початок координат. Задаються мінімальні (min) та максимальні (max) значення вхідних параметрів х1 та х2.. Складаємо план експерименту (рис. 1.3а).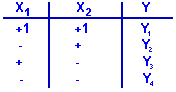 На наступному етапі перемінні кодируються. При цьому координати центру плану прирівнюються до нулю, а інтервали вар'їрування приймають за одиницю. Кодировані перемінні значно полегшують обробку результатів опитів, що в даному випадку проводиться у стандартній формі, не залежній від конкретних умов завдання.
На наступному етапі перемінні кодируються. При цьому координати центру плану прирівнюються до нулю, а інтервали вар'їрування приймають за одиницю. Кодировані перемінні значно полегшують обробку результатів опитів, що в даному випадку проводиться у стандартній формі, не залежній від конкретних умов завдання.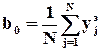
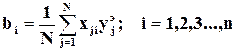
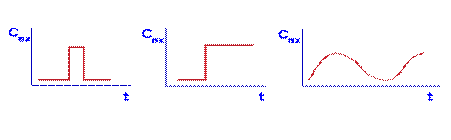 При визначення реакції об'єкту на стандартні обурення на вхід подається який-то стандартний сигнал - одиничний iмпульс, східчаста або синусоїдальна зміна вхідного параметра рис. 1.4.
При визначення реакції об'єкту на стандартні обурення на вхід подається який-то стандартний сигнал - одиничний iмпульс, східчаста або синусоїдальна зміна вхідного параметра рис. 1.4. Модель будувалася для значень iнтервалу (а в)
Модель будувалася для значень iнтервалу (а в)
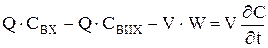 (2. 1)
(2. 1) (2. 2)
(2. 2) (2.3)
(2.3) (2.4)
(2.4)



 (2.9)
(2.9) (2.10)
(2.10)
 (2.11)
(2.11)
 – відношення усередненої теплоємністi апарату до теплоємністі реакційноі суміші ("безрозмірна теплоємність");
– відношення усередненої теплоємністi апарату до теплоємністі реакційноі суміші ("безрозмірна теплоємність"); - адіабатичний розігрів, тобто величина, що характеризує на скільки градусів розігріється реакційна суміш при повній мірі перетворення;
- адіабатичний розігрів, тобто величина, що характеризує на скільки градусів розігріється реакційна суміш при повній мірі перетворення; – адіабатичний розігрів в безрозмірной формі;
– адіабатичний розігрів в безрозмірной формі; - безрозмірний параметр тепловідвода;
- безрозмірний параметр тепловідвода; 0 - константа швидкісті реакціі при опорной температури;
0 - константа швидкісті реакціі при опорной температури; .
. (2.20)
(2.20)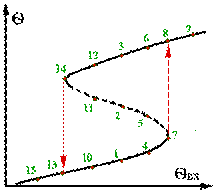 Оскільки порівняння залежності швидкості тепловідвода від параметрів (2.18) подає порівняння прямої лінії, оте при зміні параметрів,які входять в коефіціент a - qвх і qх, лінія тепловідвода буде переміщатися паралельно самої собі.
Оскільки порівняння залежності швидкості тепловідвода від параметрів (2.18) подає порівняння прямої лінії, оте при зміні параметрів,які входять в коефіціент a - qвх і qх, лінія тепловідвода буде переміщатися паралельно самої собі. Стаціонарні режими,одержані при базовому значенні qвх, позначені цифрами 1,2,3. При збільшенні qвх лінія тепловідводу зміщується праворуч.При цьому число стаціонарних режимів залишається колишнiм (позначені 4,5,6). При подальшому збільшенні qвх число с
Стаціонарні режими,одержані при базовому значенні qвх, позначені цифрами 1,2,3. При збільшенні qвх лінія тепловідводу зміщується праворуч.При цьому число стаціонарних режимів залишається колишнiм (позначені 4,5,6). При подальшому збільшенні qвх число с 


